Planteamiento del problema:
En un restaurante, las pizzas se pueden pedir en cajas de 6, 9 y 20. ¿Cuál es el mayor número de pizzas que no se pueden comprar con ninguna combinación de estas cajas?
Por ejemplo:

- Existen dos tipos de soluciones para tal problema.
- Incluyen los matemáticos y algorítmicos.
- La solución matemática se limita solo a los valores de caja dados, mientras que la solución algorítmica se puede aplicar a cualquier valor de caja.
Solución matemática:
- La combinación de 6 y 9 te dará todos los múltiplos de 3 (excepto 3 pizzas).
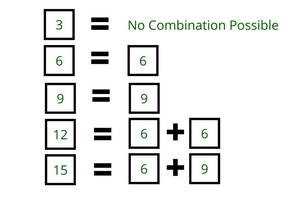
- Si un número no es un múltiplo de 3, utilice una casilla de 20. Calcule el valor restante y verifique si es un múltiplo de 3. Por ejemplo:
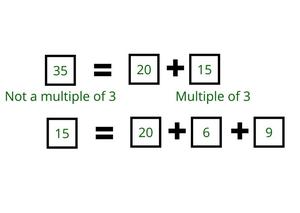
- Por lo tanto, es posible comprar 35 cajas de pizza.
- Pero no es posible comprar 28 cajas porque después de usar una caja de 20 solo quedan 8 cajas que no es el múltiplo de 3.
- De manera similar, después de usar 1 casilla de 20, si el número restante no es divisible por 3, entonces verifica si se puede usar otra casilla de 20.
- Por ejemplo:
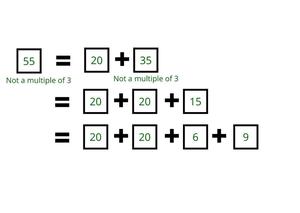
- Resta repetidamente 20 de un número dado hasta obtener un número divisible por 3.
- Este enfoque siempre funciona, porque cualquier número cuando se divide por 3 da un resto de 0, 1 o 2.
- Por ejemplo, 15 es divisible por 3, así que obtenga un resto de 0 al dividir 15 por 3.
- Ahora, si toma cualquier número que no sea un múltiplo de 3 y lo suma a 15 repetidamente y divide el resultado de la suma por 3.
- El resto se tomará como secuencia de salida como 0, 1, 2 0, 1, 2 01, 2 o 0, 2, 1 0, 2, 1 0, 2, 1.
- Desde el enfoque anterior, parece que se puede comprar cualquier cantidad de pizzas> = 40, pero hay 1 número por encima de 20 que no se puede lograr con ninguna combinación de 20, 9 y 6.
- Después de usar un máximo de 2 casillas de 20, el valor restante debe ser divisible por 3. Como se vio anteriormente, el número 3 no se puede lograr con ninguna combinación de 20, 9 y 6.
- El mayor número de pizzas que no se pueden comprar= 20+ 20+ 3= 43.
Algoritmo:
- La caja más pequeña es 6.
- Si logra 6 números consecutivos, obtenga todos los números adicionales simplemente agregando una casilla más de 6.
- Por ejemplo:
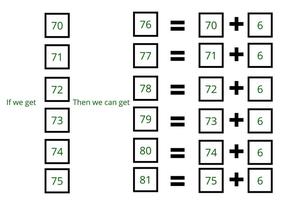
- Entonces el objetivo es encontrar esos 6 números consecutivos.
- Hagamos combinaciones para lograr un número de cajas de pizza en orden creciente.
- Al observar el patrón se tomarán 6 números consecutivos del 44 al 49.
- Por tanto, se puede conseguir cualquier número de casillas superior a 49 con la ayuda de una casilla más de 6.
- Entonces, el mayor número de casillas que no se pueden obtener con ninguna combinación de 20, 9 y 6 están presentes antes de 44, es decir, 43. Esta es la respuesta requerida.