Escriba un programa eficiente para encontrar la suma de subarreglo contiguo dentro de un arreglo unidimensional de números que tenga la suma más grande.
Algoritmo de Kadane:
Initialize:
max_so_far = INT_MIN
max_ending_here = 0
Loop for each element of the array
(a) max_ending_here = max_ending_here + a[i]
(b) if(max_so_far < max_ending_here)
max_so_far = max_ending_here
(c) if(max_ending_here < 0)
max_ending_here = 0
return max_so_far
Explicación:
la idea simple del algoritmo de Kadane es buscar todos los segmentos contiguos positivos de la array (para esto se usa max_ending_here). Y realice un seguimiento de la suma máxima de segmentos contiguos entre todos los segmentos positivos (para esto se usa max_so_far). Cada vez que obtengamos una suma positiva, compárela con max_so_far y actualice max_so_far si es mayor que max_so_far
Lets take the example:
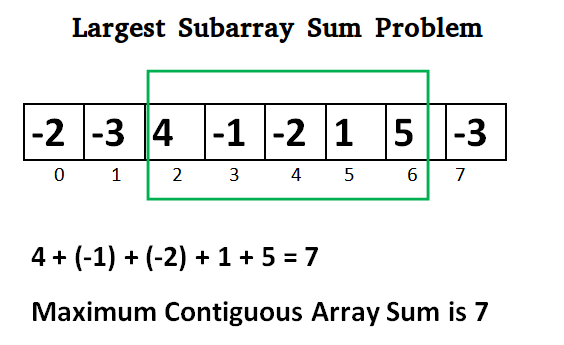
{-2, -3, 4, -1, -2, 1, 5, -3}
max_so_far = max_ending_here = 0
for i=0, a[0] = -2
max_ending_here = max_ending_here + (-2)
Set max_ending_here = 0 because max_ending_here < 0
for i=1, a[1] = -3
max_ending_here = max_ending_here + (-3)
Set max_ending_here = 0 because max_ending_here < 0
for i=2, a[2] = 4
max_ending_here = max_ending_here + (4)
max_ending_here = 4
max_so_far is updated to 4 because max_ending_here greater
than max_so_far which was 0 till now
for i=3, a[3] = -1
max_ending_here = max_ending_here + (-1)
max_ending_here = 3
for i=4, a[4] = -2
max_ending_here = max_ending_here + (-2)
max_ending_here = 1
for i=5, a[5] = 1
max_ending_here = max_ending_here + (1)
max_ending_here = 2
for i=6, a[6] = 5
max_ending_here = max_ending_here + (5)
max_ending_here = 7
max_so_far is updated to 7 because max_ending_here is
greater than max_so_far
for i=7, a[7] = -3
max_ending_here = max_ending_here + (-3)
max_ending_here = 4
Programa:
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static int maxSubArraySum(int []a)
{
int size = a.Length;
int max_so_far = int.MinValue,
max_ending_here = 0;
for (int i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i];
if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
if (max_ending_here < 0)
max_ending_here = 0;
}
return max_so_far;
}
// Driver code
public static void Main ()
{
int [] a = {-2, -3, 4, -1, -2, 1, 5, -3};
Console.Write("Maximum contiguous sum is " +
maxSubArraySum(a));
}
}
// This code is contributed by Sam007_
Producción:
Maximum contiguous sum is 7
Complejidad de tiempo: O(N), donde N representa el tamaño de la array dada.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Otro enfoque:
C#
static int maxSubArraySum(int[] a, int size)
{
int max_so_far = a[0], max_ending_here = 0;
for (int i = 0; i < size; i++) {
max_ending_here = max_ending_here + a[i];
if (max_ending_here < 0)
max_ending_here = 0;
/* Do not compare for all
elements. Compare only
when max_ending_here > 0 */
else if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
}
return max_so_far;
}
// This code is contributed
// by ChitraNayal
Complejidad de tiempo: O(n), donde n representa el tamaño de la array dada.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Paradigma algorítmico: Programación dinámica
A continuación se muestra otra implementación sencilla sugerida por Mohit Kumar . La implementación maneja el caso cuando todos los números en la array son negativos.
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static int maxSubArraySum(int []a, int size)
{
int max_so_far = a[0];
int curr_max = a[0];
for (int i = 1; i < size; i++)
{
curr_max = Math.Max(a[i], curr_max+a[i]);
max_so_far = Math.Max(max_so_far, curr_max);
}
return max_so_far;
}
// Driver code
public static void Main ()
{
int []a = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = a.Length;
Console.Write("Maximum contiguous sum is "
+ maxSubArraySum(a, n));
}
}
// This code is contributed by Sam007_
Producción:
Maximum contiguous sum is 7
Complejidad de tiempo: O(N), donde N representa el tamaño de la array dada.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.
Para imprimir el subarreglo con la suma máxima, mantenemos índices siempre que obtengamos la suma máxima.
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static void maxSubArraySum(int []a,
int size)
{
int max_so_far = int.MinValue,
max_ending_here = 0, start = 0,
end = 0, s = 0;
for (int i = 0; i < size; i++)
{
max_ending_here += a[i];
if (max_so_far < max_ending_here)
{
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0)
{
max_ending_here = 0;
s = i + 1;
}
}
Console.WriteLine("Maximum contiguous " +
"sum is " + max_so_far);
Console.WriteLine("Starting index " +
start);
Console.WriteLine("Ending index " +
end);
}
// Driver code
public static void Main()
{
int []a = {-2, -3, 4, -1,
-2, 1, 5, -3};
int n = a.Length;
maxSubArraySum(a, n);
}
}
// This code is contributed
// by anuj_67.
Producción:
Maximum contiguous sum is 7 Starting index 2 Ending index 6
El algoritmo de Kadane se puede ver tanto como codicioso como como DP. Como podemos ver, mantenemos una suma continua de enteros y cuando se vuelve menor que 0, la restablecemos a 0 (parte codiciosa). Esto se debe a que continuar con una suma negativa es mucho peor que reiniciar con un nuevo rango. Ahora también se puede ver como un DP, en cada etapa tenemos 2 opciones: tomar el elemento actual y continuar con la suma anterior O reiniciar un nuevo rango. Estas dos opciones están siendo atendidas en la implementación.
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(1)
Ahora intente la siguiente pregunta
Dada una array de enteros (posiblemente algunos elementos negativos), escriba un programa C para encontrar el *producto máximo* posible multiplicando ‘n’ enteros consecutivos en la array donde n ≤ ARRAY_SIZE. Además, imprima el punto de inicio del subarreglo de producto máximo.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA