El procedimiento para resolver y encontrar la función de salida del multiplexor dado es bastante simple. Primero discutiremos el procedimiento y luego lo ilustraremos con ejemplos.
Procedimiento:
- En primer lugar, se construye la tabla de verdad para el multiplexor dado.
- Las líneas seleccionadas en el multiplexor se consideran como entrada para la tabla de verdad.
- La salida en la tabla de verdad puede ser de cuatro formas, es decir (0, 1, Q, Q’).
- Ahora, con la ayuda de la tabla de verdad, encontramos la expresión extendida.
- Luego, la expresión se minimiza usando reglas algebraicas booleanas.
- La función final puede estar en forma de expresión o en forma SOP o POS.
Ejemplo-1:
dado que MUX está siguiendo,
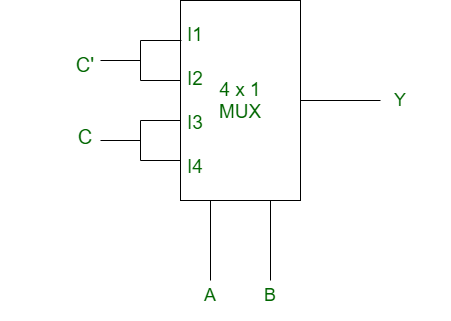
Explicación :
- Paso 1: Primero dibuja la tabla de verdad. Para la tabla de verdad, seleccione las líneas A y B como entrada.
Según el circuito,I0 = C' (hence first row of truth table will be C') I1 = C' I2 = C I3 = C
I0, I1, I2, I3 se consideran como salida de la 1.ª, 2.ª, 3.ª y 4.ª fila de la tabla de verdad, respectivamente.

- Paso-2: Ahora encontraremos la expresión de Y:
Y = A'B'C' + A'BC' + AB'C+ ABC = A'C'(B' + B) + AC(B' + B) = A'C' + AC
Ejemplo-2:
dado MUX,
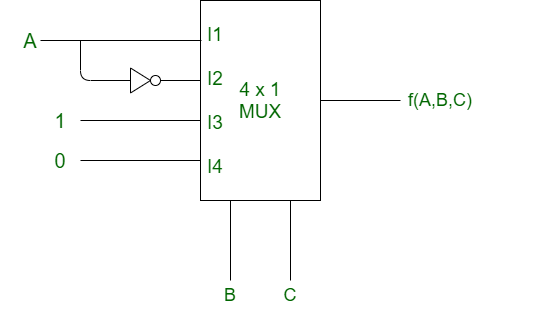
Explicación :
- Paso 1: la tabla de verdad es la siguiente. Para la tabla de verdad, seleccione las líneas B y C.
Según el circuito,I0 = A (hence first row of truth table will be A) I1 = A' I2 = 1 I3 = 0
I0, I1, I2, I3 se consideran como salida de la 1.ª, 2.ª, 3.ª y 4.ª fila de la tabla de verdad, respectivamente.

- Paso 2: ahora encontraremos la salida:
f(A, B, C) = AB'C' + A'B'C+ BC'.1 = AB'C' + A'B'C+ BC'(A + A') = AB'C' + A'B'C+ ABC' + A'BC' = 100 001 110 010 = m(1, 2, 4, 6)