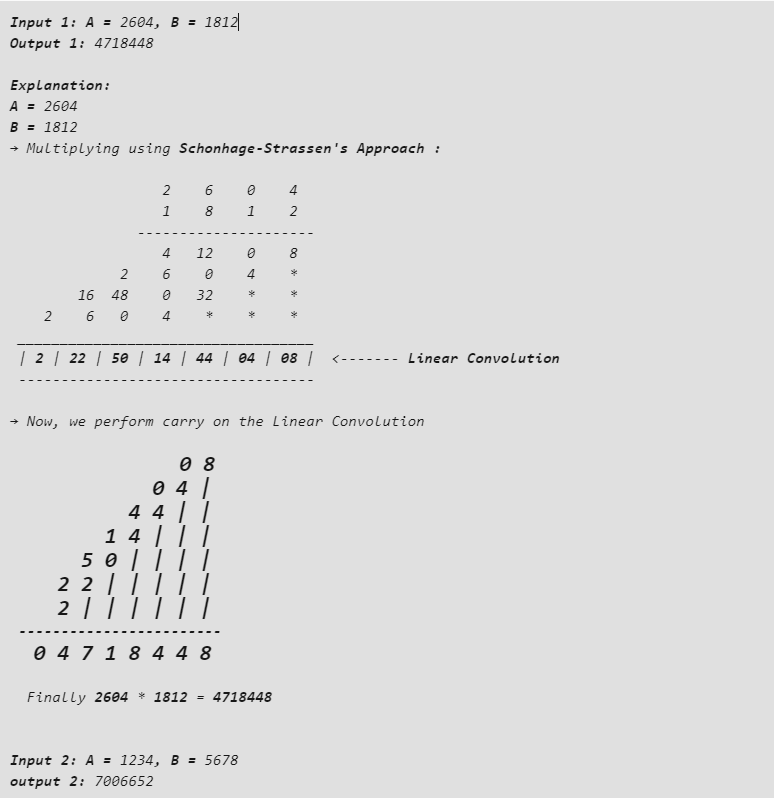
El algoritmo de Schonhage-Strassen es una de las formas más rápidas de multiplicar valores enteros muy grandes (30000 a 150000 dígitos decimales). Este algoritmo fue desarrollado por Arnold Schönhage y Volker Strassen . Aunque el algoritmo de Furer es más rápido que el algoritmo de Schonhage-Strassen, no hay aplicaciones prácticas para él, excepto los algoritmos galácticos (probablemente no se usan para ningún dato presente en la tierra). Por lo tanto, el algoritmo de Schonhage-Strassen se considera el mejor para multiplicar valores enteros grandes.
En este enfoque de multiplicación, los dos números enteros se multiplican primero sin realizar el acarreo. El conjunto de resultados entonces obtenido se llama Convolución Acíclica o Convolución Lineal . Luego llevamos a cabo las columnas individuales de la convolución lineal.
Ejemplos:
Java
// Java program to implement Schonhage-Strassen's
// Multiplication Algorithm
import java.io.*;
class GFG {
// two class level variables to
// store the given values
static long a, b;
// class level array to store the LinearConvolution
static int[] linearConvolution;
// an integer variable to determine
// the length of the LinearConvolution
static int length;
// to count the no.of digits in each of
// the given values a and b
static int countDigits(long num)
{
// an integer variable initialized to
// 0 to store the no.of digits
int count = 0;
// as long as the number is
// greater than 0, divide it by 10
// and increment the count
while (num > 0) {
num /= 10;
count++;
}
// return the count when number becomes 0
return count;
}
// to perform schonhage-Strassen's Multiplication
static void schonhageStrassenMultiplication()
{
// first find the LinearConvolution
findLinearConvolution();
// Then perform carry on it
performCarry();
}
// to find LinearConvolution
static void findLinearConvolution()
{
// no.of digits in first number (a)
int aDigits = countDigits(a);
// no.of digits in second number (b)
int bDigits = countDigits(b);
// a temporary variable to store the value of a
long temp = a;
// length of the LinearConvolution is
// 1 less than the no.of Digits in a +
// no.of digits in b
length = aDigits + bDigits - 1;
linearConvolution = new int[length];
for (int i = 0; i < aDigits; i++, b /= 10) {
a = temp;
for (int j = 0; j < bDigits; j++, a /= 10) {
// multiply the current digit of a with
// current digit of b and store in
// LinearConvolution
linearConvolution[i + j]
+= (b % 10) * (a % 10);
}
}
System.out.print("The Linear Convolution is: [ ");
for (int i = length - 1; i >= 0; i--) {
// print the LinearConvolution array
System.out.print(linearConvolution[i] + " ");
}
System.out.println("]");
}
// to perform carry on the obtained LinearConvolution
static void performCarry()
{
// initialize product to 0
long product = 0;
int carry = 0, base = 1;
// for every value in the LinearConvolution
for (int i = 0; i < length; i++) {
linearConvolution[i] += carry;
// add the product of base and units digit of
// LinearConvolution[i] to the product
product
= product
+ (base * (linearConvolution[i] % 10));
// now LinearConvolution[i]/10
// will become the carry
carry = linearConvolution[i] / 10;
base *= 10;
}
System.out.println("\nThe Product is : " + product);
}
// Driver method
public static void main(String[] args)
{
// initialize the two declared class variables with
// the desired values
a = 2604;
b = 1812;
// call schonhageStrassenMultiplication() method
schonhageStrassenMultiplication();
}
}
The Linear Convolution is: [ 2 22 50 14 44 4 8 ] The Product is : 4718448
Complejidad de tiempo: O(n. log n . log log n )