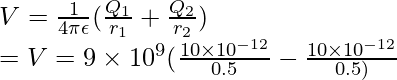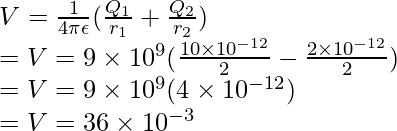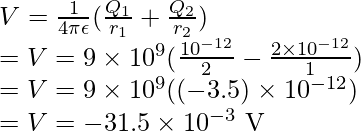Potencial eléctrico debido a una carga puntual

Posted on by Rudeus Greyrat

Las fuerzas eléctricas son responsables de casi todas las reacciones químicas dentro del cuerpo humano. Estas reacciones químicas ocurren cuando los átomos y sus cargas chocan entre sí. En este proceso, se forman algunas moléculas y otras cambian de forma. Los cuerpos cargados experimentan fuerzas eléctricas cuando se encuentran bajo la influencia de un campo eléctrico. Estas fuerzas dependen de la dirección del campo eléctrico y de la carga colocada en ese campo. Cuando las cargas se mueven en el campo eléctrico, estas fuerzas realizan trabajo sobre la carga y eso se almacena en forma de energía potencial electrostática. Veamos los conceptos de potencial electrostático y energía potencial electrostática en detalle. 

Energia potencial electrica

La energía potencial eléctrica es la energía que se requiere para mover una carga contra un campo eléctrico. Cuando una carga se mantiene en un campo eléctrico, experimenta una fuerza. Entonces, para movernos en contra de la fuerza, necesitamos hacer trabajo y ese trabajo se almacena en la carga en forma de energía potencial eléctrica. En la figura que se muestra a continuación, hay una placa enorme que está cargada negativamente y tiene algunas cargas positivas adheridas. 

En la figura, cuando las cargas positivas se separan de la placa cargada negativamente, experimentan fuerza. Entonces, para separar las cargas de los lugares, se necesita trabajar contra la fuerza que actúa sobre ellos. En este proceso, la energía potencial se almacena en ellos. Cuando se liberan estas cargas, comienzan a correr hacia la placa cargada negativamente. Entonces, en esta situación, la energía potencial almacenada en estas cargas se convierte en energía cinética. 

Para un sistema de dos cargas con cargas q y Q dadas en la figura anterior, el cambio en la energía potencial eléctrica al llevar la carga q, de A a B está dado por, 

W_{AB}=\frac{Qq}{4 \pi \epsilon}(\frac{1}{r_B} - \frac{1}{r_A})

Potencial eléctrico 

El potencial eléctrico se define como la diferencia de energía potencial por unidad de carga entre dos lugares. Para verificar la diferencia en el potencial eléctrico entre dos posiciones bajo la influencia de un campo eléctrico, se pregunta cuánto cambiará la energía potencial de una unidad de carga positiva si esa carga se mueve de esta posición a la otra posición. se denota por V, 

V = \frac{\text{P.E}}{q}

En una situación similar a la descrita en el apartado anterior. La carga positiva está cerca de la placa, cuanto más lejos esté la carga de esta placa, mayor será el trabajo realizado sobre la carga. Entonces, en este caso, decimos que el potencial cerca de la placa cargada negativamente es bajo y, a medida que uno se aleja, el potencial aumenta. Ahora comprendamos el potencial debido a una carga puntual en términos formales. 

Potencial eléctrico debido a carga puntual

Considere una carga puntual como se muestra en la siguiente figura. Observe que en la figura hay algunos círculos concéntricos. Estos círculos concéntricos representan el contorno equipotencial. Eso significa, que en todos los puntos en un solo contorno. El potencial es el mismo. El objetivo es calcular el potencial eléctrico debido a esta carga puntual entre dos puntos A y B. 

La diferencia de potencial eléctrico también se llama voltaje y se mide en unidades de voltios. 

tensión AB = diferencia de potencial eléctrico AB = \frac{U_B}{q} - \frac{U_A}{q}  

El potencial hasta ahora se ha definido como una diferencia; se requiere una formulación en términos de potencial absoluto. La formulación anterior se modificará para dar con esta nueva definición. En infinito, se supone que el campo eléctrico y el potencial son cero. Ahora, el potencial en cada punto se calculará con respecto al infinito, y dará un valor absoluto del potencial. 

Ahora, r B =  \infty y r A

voltaje AB = \frac{U_B}{q} - \frac{U_A}{q}  

                  = \frac{1}{4\pi \epsilon }\frac{q}{r_A} - \frac{1}{4\pi \epsilon }\frac{q}{r_B}

Ahora, r B = \infty

              = \frac{1}{4\pi \epsilon }\frac{q}{r_A} - \frac{1}{4\pi \epsilon }\frac{q}{\infty}

              = \frac{1}{4\pi \epsilon }\frac{q}{r_A}

Superposición de potencial eléctrico 

Para un sistema de cargas puntuales, el potencial total en un punto viene dado por la suma algebraica del potencial de las cargas individuales en ese punto. Por ejemplo, en un sistema que contiene cargas Q 1, Q 2 y Q 3 a una distancia de r 1 , r 2 y r 3 de un punto. Entonces, el potencial en este punto estará dado por la siguiente ecuación, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

Problemas de muestra

Pregunta 1: Encuentra el potencial a una distancia de 1 m debido a una carga de 2pC. 

Responder: 

El potencial debido a una carga puntual está dado por, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

Aquí, q = 2 pC = 2 x 10 -12 C y r = 1 m. 

Reemplazando los valores en esta ecuación, 

V = \frac{1}{4\pi \epsilon }\frac{q}{r}

⇒V = 9 \times 10^{9} .\frac{2 \times 10^{-12}}{1}

⇒ V= 9 × 10 9 × 2 × 10 -12

⇒ V= 18 × 10 -3

Pregunta 2: Encuentra el potencial a una distancia de 0,5 m debido a una carga de 10pC. 

Responder: 

El potencial debido a una carga puntual está dado por, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

Aquí, q = 10 pC = 10 x 10 -12 C y r = 0,5 m. 

Reemplazando los valores en esta ecuación, 

V = \frac{1}{4\pi \epsilon }\frac{q}{r}

⇒V = 9 \times 10^{9} .\frac{10 \times 10^{-12}}{0.5}

⇒ V= 9 × 10 9 × 2 x 10 -11

⇒ V= 18 x 10 -2

Pregunta 3: Encuentra la energía potencial a una distancia de 0,5 m debido a una carga de 10pC y -10pC. 

Responder: 

El potencial debido a una carga puntual está dado por, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

Aquí, q 1 = 10 pC = 10 x 10 -12 C, q 2 = -10 pC = -10 x 10 -12 C y r = 0,5 m. 

Como hay dos cargas en el sistema, el potencial total vendrá dado por la ecuación de superposición. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

Por dos cargos, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

Reemplazando los valores en esta ecuación, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10 \times 10^{-12}}{0.5} - \frac{10 \times 10^{-12}}{0.5)}

⇒V= 0

Pregunta 4: Encuentra la energía potencial a una distancia de 2 m debido a una carga de 10pC y -2pC. 

Responder: 

El potencial debido a una carga puntual está dado por, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

Aquí, q 1 = 10 pC = 10 x 10 -12 C, q 2 = -10 pC = -2 x 10 -12 C y r = 2 m. 

Como hay dos cargas en el sistema, el potencial total vendrá dado por la ecuación de superposición. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

Por dos cargos, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

Reemplazando los valores en esta ecuación, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10 \times 10^{-12}}{2} - \frac{2 \times 10^{-12}}{2}) \\ = V = 9 \times 10^9(4 \times 10^{-12}) \\ = V = 36 \times 10^{-3}

⇒ V= 36 × 10 -3 V

Pregunta 5: Dos cargas se mantienen en esquinas opuestas de rectángulos como se muestra en la figura. Encuentre el potencial en la esquina entre ellos. 

Responder: 

El potencial debido a una carga puntual está dado por, 

\frac{1}{4\pi \epsilon }\frac{q}{r}

Aquí, q 1 = 1 pC = 10 -12 C, q 2 = -2 pC = -2 x 10 -12 C y r 1 = 2 m y r 2 = 1 m. 

Como hay dos cargas en el sistema, el potencial total vendrá dado por la ecuación de superposición. 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} + \frac{Q_3}{r_3} )

Por dos cargos, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} )

Reemplazando los valores en esta ecuación, 

V = \frac{1}{4\pi \epsilon }(\frac{Q_1}{r_1} + \frac{Q_2}{r_2} ) \\ = V = 9 \times 10^9(\frac{10^{-12}}{2} - \frac{2 \times 10^{-12}}{1}) \\ = V = 9 \times 10^9((-3.5) \times 10^{-12}) \\ = V = -31.5 \times 10^{-3} \text{ V}

⇒ V= 36 × 10 -3 V

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *