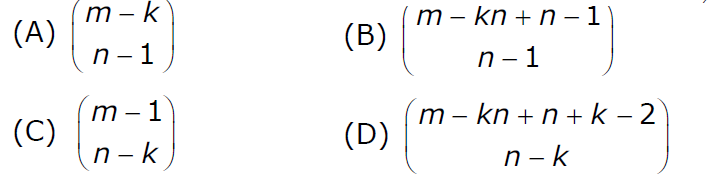PUERTA | PUERTA-CS-2003 | Pregunta 34

Se colocarán m bolas idénticas en n bolsas distintas. Se sabe que m ≥ kn, donde k es un número natural ≥ 1. ¿De cuántas maneras se pueden colocar las bolas en las bolsas si cada bolsa debe contener al menos k bolas?

(A) A
(B) B
(C) C
(D) D

Respuesta: (B)
Explicación: Esta es una aplicación muy simple de estrellas y barras . Como queremos al menos k bolas en cada bolsa, primero ponemos kn bolas en bolsas, k bolas en cada bolsa. Ahora nos quedan m – kn bolas, y tenemos que ponerlas en n bolsas de modo que cada bolsa pueda recibir 0 o más bolas. Entonces, aplicando el teorema 2 de estrellas y barras con m – nk estrellas y n barras, obtenemos varias formas de ser ^m−kn+n-1 C _n−1 . Entonces la opción (B) es correcta.

Fuente: http://www.cse.iitd.ac.in/~mittal/gate/gate_math_2003.html
Prueba de esta pregunta