Dada una array, arr[] de tamaño N , la tarea es encontrar el número de sub-arrays que terminan en arr[i] y arr[i] es el elemento mínimo de esa sub-array.
Ejemplos:
Entrada: arr[] = {3, 1, 2, 4}
Salida: 1 2 1 1
Explicación:
Subarreglos que terminan en 3 donde 3 es el elemento mínimo = {3}
Subarreglos que terminan en 1 donde 1 es el elemento mínimo = {3 , 1}, {1}
Subarreglos que terminan en 2 donde 2 es el elemento mínimo = {2}
Subarreglos que terminan en 4 donde 4 es el elemento mínimo = {4}
Entrada: arr[] = {5, 4, 3, 2, 1}
Salida: 1 2 3 4 5
Enfoque: la idea es utilizar el enfoque utilizado para encontrar el siguiente elemento mayor manteniendo una pila . El enfoque paso a paso para el problema es:
- Empuje el primer elemento (arr[0]) de la array con el conteo como 1 en la pila porque el primer elemento será la propia sub-array que termina con el elemento actual arr[0] y el mínimo de la subarray
- Luego, para cada elemento arr[i] en la array-
- Extraiga los elementos de la pila hasta que la parte superior de la pila sea mayor que el elemento actual y agregue el recuento del elemento extraído en el recuento del elemento actual.
- Empuje el elemento actual y el conteo como un par en la pila.
Por ejemplo: Para arr[] = {3, 1, 2, 4},
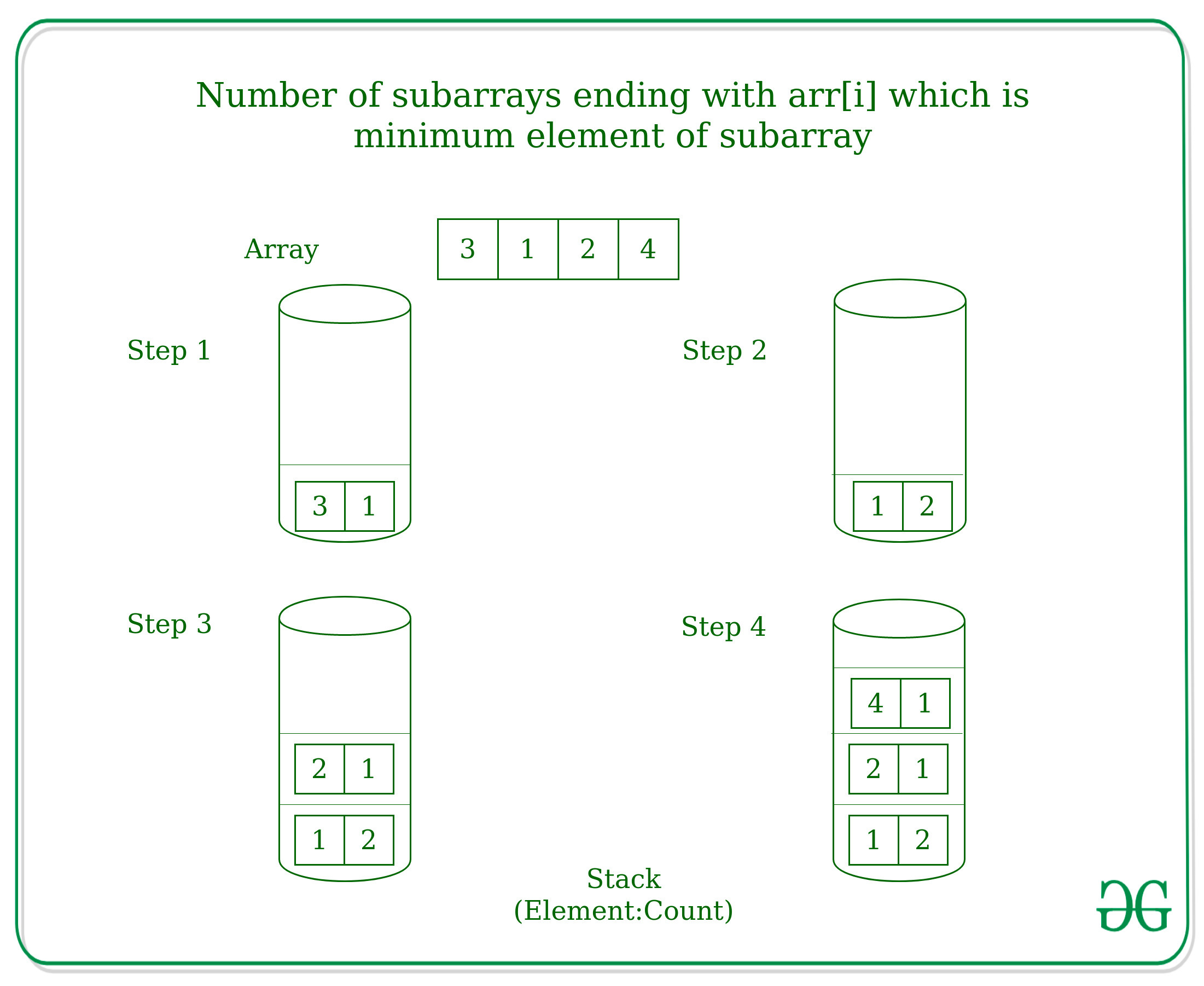
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
#include <bits/stdc++.h>
using namespace std;
// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
int min_subarray(int a[], int n)
{
stack<pair<int, int> > st;
for (int i = 0; i < n; ++i) {
// There exists a subarray of
// size 1 for each element
int count = 1;
// Remove all greater elements
while (!st.empty() &&
st.top().first > a[i]) {
// Increment the count
count += st.top().second;
// Remove the element
st.pop();
}
// Push the current element
// and it's count
st.push({ a[i], count });
cout << count << " ";
}
}
// Driver Code
int main()
{
int a[] = {5, 4, 3, 2, 1};
int n = sizeof(a) / sizeof(a[0]);
min_subarray(a, n);
return 0;
}
Java
// Java implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
import java.util.*;
import java.lang.*;
import java.io.*;
class Main
{
static class Pair
{
int first;
int second;
public Pair(int x, int y)
{
this.first = x;
this.second = y;
}
}
// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
static void min_subarray(int []a, int n)
{
Stack<Pair> st = new Stack<Pair>();
for (int i = 0; i < n; ++i)
{
// There exists a subarray of
// size 1 for each element
int count = 1;
// Remove all greater elements
while (st.empty() == false &&
st.peek().first > a[i])
{
// Increment the count
count += st.peek().second;
// Remove the element
st.pop();
}
// Push the current element
// and it's count
st.push(new Pair (a[i], count ));
System.out.print(count + " ");
}
}
// Driver Code
public static void main(String []args)
{
int []a = {5, 4, 3, 2, 1};
int n = a.length;
min_subarray(a, n);
}
}
// This code is contributed by tufan_gupta2000
Python3
# Python3 implementation to find the number # of sub-arrays ending with arr[i] which # is the minimum element of the subarray # Function to find the number # of sub-arrays ending with arr[i] which # is the minimum element of the subarray def min_subarray(a, n) : st = []; for i in range(n) : # There exists a subarray of # size 1 for each element count = 1; # Remove all greater elements while len(st) != 0 and st[-1][0] > a[i] : # Increment the count count += st[-1][1]; # Remove the element st.pop(); # Push the current element # and it's count st.append(( a[i], count )); print(count,end= " "); # Driver Code if __name__ == "__main__" : a = [5, 4, 3, 2, 1]; n = len(a); min_subarray(a, n); # This code is contributed by AnkitRai01
C#
// C# implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
using System;
using System.Collections.Generic;
class GFG
{
class Pair
{
public int first;
public int second;
public Pair(int x, int y)
{
this.first = x;
this.second = y;
}
}
// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
static void min_subarray(int []a, int n)
{
Stack<Pair> st = new Stack<Pair>();
for (int i = 0; i < n; ++i)
{
// There exists a subarray of
// size 1 for each element
int count = 1;
// Remove all greater elements
while (st.Count != 0 &&
st.Peek().first > a[i])
{
// Increment the count
count += st.Peek().second;
// Remove the element
st.Pop();
}
// Push the current element
// and it's count
st.Push(new Pair (a[i], count ));
Console.Write(count + " ");
}
}
// Driver Code
public static void Main(String []args)
{
int []a = {5, 4, 3, 2, 1};
int n = a.Length;
min_subarray(a, n);
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// Javascript implementation to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
// Function to find the number
// of sub-arrays ending with arr[i] which
// is the minimum element of the subarray
function min_subarray(a, n)
{
var st = [];
for (var i = 0; i < n; ++i) {
// There exists a subarray of
// size 1 for each element
var count = 1;
// Remove all greater elements
while (st.length!=0 &&
st[st.length-1][0] > a[i]) {
// Increment the count
count += st[st.length-1][1];
// Remove the element
st.pop();
}
// Push the current element
// and it's count
st.push([a[i], count]);
document.write( count + " ");
}
}
// Driver Code
var a = [5, 4, 3, 2, 1];
var n = a.length;
min_subarray(a, n);
// This code is contributed by itsok.
</script>
1 2 3 4 5
Complejidad de tiempo: O (n), donde n es el tamaño de la array dada.
Complejidad espacial : O(n)
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA