Dada una array cuadrada de orden impar N. La tarea es encontrar la longitud del lado del cuadrado más grande formado en la array. Se dice que un cuadrado en array está formado si todos los elementos de su perímetro son iguales y su centro es el centro de la array. El centro de la array también es un cuadrado con lado de longitud 1.
Ejemplos :
Input : matrix[][] = {2, 3, 0,
0, 2, 0,
0, 1, 1}
Output : 1
Input : matrix[][] = {2, 2, 2,
2, 1, 2,
2, 2, 2}
Output : 3
El centro de cualquier array de orden impar es el elemento con índice i = j = n/2 . Ahora, para encontrar el cuadrado más grande en la array, verifique todos los elementos circundantes desde el centro que están a la misma distancia. Para un cuadrado que está a una unidad de distancia del centro, verifique todos los elementos que están en la fila y columna n/2-i y n/2+i , también la diferencia de n/2 y cualquiera de los índices del elemento no exceda i . Encuentre el formato de un cuadrado con diferentes longitudes de lado posibles en el siguiente ejemplo.
x x x x x x y y y x x y c y x x y y y x x x x x x
Puntos a tener en cuenta:
- Como elemento central también es una forma de cuadrado, la longitud mínima posible del lado es 1.
- El cuadrado más largo puede estar con todos los elementos presentes en la primera fila y la primera columna, por lo tanto, la longitud lateral máxima posible es
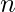
Algoritmo:
- Iterar sobre i=0 a n/2
- itere sobre la columna i a ni-1 para la fila i y ni-1
y viceversa y verifique si todos los elementos son iguales o no. - En caso afirmativo, la longitud del cuadrado es n-2*i.
- De lo contrario, vaya a la siguiente iteración
- itere sobre la columna i a ni-1 para la fila i y ni-1
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find max possible side-length
// of a square in a given matrix
#include <bits/stdc++.h>
#define n 5
using namespace std;
// Function to return side-length of square
int largestSideLen(int matrix[][n])
{
int result = 1;
// Traverse the matrix
for (int i = 0; i < n / 2; i++) {
int element = matrix[i][i];
int isSquare = 1;
for (int j = i; j < n - i; j++) {
// for row i
if (matrix[i][j] != element)
isSquare = 0;
// for row n-i-1
if (matrix[n - i - 1][j] != element)
isSquare = 0;
// for column i
if (matrix[j][i] != element)
isSquare = 0;
// for column n-i-1
if (matrix[j][n - i - 1] != element)
isSquare = 0;
}
if (isSquare)
return n - 2 * i;
}
// Return result
return result;
}
// Driver program
int main()
{
int matrix[n][n] = { 1, 1, 1, 1, 1,
1, 2, 2, 2, 1,
1, 2, 1, 2, 1,
1, 2, 2, 2, 1,
1, 1, 1, 1, 1 };
cout << largestSideLen(matrix);
return 0;
}
Java
// Java program to find max possible side-length
// of a square in a given matrix
import java.io.*;
class GFG {
static int n = 5;
// Function to return side-length of square
static int largestSideLen(int matrix[][])
{
int result = 1;
// Traverse the matrix
for (int i = 0; i < (n / 2); i++) {
int element = matrix[i][i];
int isSquare = 1;
for (int j = i; j < n - i; j++) {
// for row i
if (matrix[i][j] != element)
isSquare = 0;
// for row n-i-1
if (matrix[n - i - 1][j] != element)
isSquare = 0;
// for column i
if (matrix[j][i] != element)
isSquare = 0;
// for column n-i-1
if (matrix[j][n - i - 1] != element)
isSquare = 0;
}
if (isSquare > 0)
return n - (2 * i);
}
// Return result
return result;
}
// Driver program
public static void main (String[] args) {
int matrix[][] = {{ 1, 1, 1, 1, 1},
{1, 2, 2, 2, 1},
{1, 2, 1, 2, 1},
{1, 2, 2, 2, 1},
{1, 1, 1, 1, 1 }};
System.out.println (largestSideLen(matrix));
}
}
Python3
# Python 3 program to find max possible # side-length of a square in a given matrix n = 5 # Function to return side-length of square def largestSideLen(matrix): result = 1 # Traverse the matrix for i in range(int(n / 2)): element = matrix[i][i] isSquare = 1 for j in range(i, n - i): # for row i if (matrix[i][j] != element): isSquare = 0 # for row n-i-1 if (matrix[n - i - 1][j] != element): isSquare = 0 # for column i if (matrix[j][i] != element): isSquare = 0 # for column n-i-1 if (matrix[j][n - i - 1] != element): isSquare = 0 if (isSquare): return n - 2 * i # Return result return result # Driver Code if __name__ == '__main__': matrix = [[1, 1, 1, 1, 1], [1, 2, 2, 2, 1], [1, 2, 1, 2, 1], [1, 2, 2, 2, 1], [1, 1, 1, 1, 1]] print(largestSideLen(matrix)) # This code is contributed by # Surendra_Gangwar
C#
// C# program to find max possible side-length
// of a square in a given matrix
using System;
public class GFG{
static int n = 5;
// Function to return side-length of square
static int largestSideLen(int [,]matrix)
{
int result = 1;
// Traverse the matrix
for (int i = 0; i < (n / 2); i++) {
int element = matrix[i,i];
int isSquare = 1;
for (int j = i; j < n - i; j++) {
// for row i
if (matrix[i,j] != element)
isSquare = 0;
// for row n-i-1
if (matrix[n - i - 1,j] != element)
isSquare = 0;
// for column i
if (matrix[j,i] != element)
isSquare = 0;
// for column n-i-1
if (matrix[j,n - i - 1] != element)
isSquare = 0;
}
if (isSquare > 0)
return n - (2 * i);
}
// Return result
return result;
}
// Driver program
static public void Main (){
int [,]matrix = {{ 1, 1, 1, 1, 1},
{1, 2, 2, 2, 1},
{1, 2, 1, 2, 1},
{1, 2, 2, 2, 1},
{1, 1, 1, 1, 1 }};
Console.WriteLine(largestSideLen(matrix));
}
}
PHP
<?php
// PHP program to find max possible
// side-length of a square in a given matrix
// Function to return side-length of square
function largestSideLen($matrix)
{
$n = 5;
$result = 1;
// Traverse the matrix
for ($i = 0; $i < ($n / 2); $i++)
{
$element = $matrix[$i][$i];
$isSquare = 1;
for ($j = $i; $j < ($n - $i); $j++)
{
// for row i
if ($matrix[$i][$j] != $element)
$isSquare = 0;
// for row n-i-1
if ($matrix[$n - $i - 1][$j] != $element)
$isSquare = 0;
// for column i
if ($matrix[$j][$i] != $element)
$isSquare = 0;
// for column n-i-1
if ($matrix[$j][$n - $i - 1] != $element)
$isSquare = 0;
}
if ($isSquare)
return ($n - 2 * $i);
}
// Return result
return $result;
}
// Driver Code
$matrix = array( 1, 1, 1, 1, 1,
1, 2, 2, 2, 1,
1, 2, 1, 2, 1,
1, 2, 2, 2, 1,
1, 1, 1, 1, 1 );
echo largestSideLen($matrix);
// This code is contributed by Sachin
?>
Javascript
<script>
// Javascript program to find max
// possible side-length
// of a square in a given matrix
const n = 5;
// Function to return
// side-length of square
function largestSideLen(matrix)
{
let result = 1;
// Traverse the matrix
for (let i = 0; i < parseInt(n / 2); i++)
{
let element = matrix[i][i];
let isSquare = 1;
for (let j = i; j < n - i; j++) {
// for row i
if (matrix[i][j] != element)
isSquare = 0;
// for row n-i-1
if (matrix[n - i - 1][j] != element)
isSquare = 0;
// for column i
if (matrix[j][i] != element)
isSquare = 0;
// for column n-i-1
if (matrix[j][n - i - 1] != element)
isSquare = 0;
}
if (isSquare)
return n - 2 * i;
}
// Return result
return result;
}
// Driver program
let matrix = [ [1, 1, 1, 1, 1],
[1, 2, 2, 2, 1],
[1, 2, 1, 2, 1],
[1, 2, 2, 2, 1],
[1, 1, 1, 1, 1 ]];
document.write(largestSideLen(matrix));
</script>
5
Publicación traducida automáticamente
Artículo escrito por Shivam.Pradhan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA