Ya conocemos Finite Automata que se puede usar para aceptar lenguajes regulares y Pushdown Automata que se pueden usar para reconocer Context Free Languages.
Queue Automata (QDA) es un autómata no determinista que es similar a Pushdown Automata pero tiene una cola en lugar de una pila que ayuda a Queue automata a reconocer idiomas más allá de los idiomas libres de contexto.
Un QDA es una tupla de 6![]()
Dónde
- Q es el conjunto de estados finitos.
 es el conjunto de alfabetos de entrada finitos.
es el conjunto de alfabetos de entrada finitos. es el conjunto de alfabetos de cola finitos.
es el conjunto de alfabetos de cola finitos.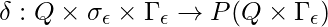 .
.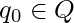 es el estado inicial.
es el estado inicial.- F
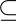 Q es el conjunto de estados de aceptación.
Q es el conjunto de estados de aceptación.
Aceptación de una string
Un QDA ![]() acepta entrada
acepta entrada ![]() si
si ![]() se puede escribir como
se puede escribir como ![]() , donde cada uno
, donde cada uno ![]()
![]() de ellos existen estados
de ellos existen estados ![]() y strings
y strings ![]() , de modo que satisfagan las siguientes condiciones:
, de modo que satisfagan las siguientes condiciones:
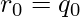 y
y 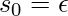 .
.- para

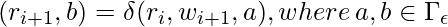 y
y 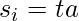 y
y 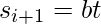 y
y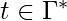
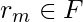
Ejemplo:
definir los autómatas de cola para el idioma![]()
Solución:
Q = {q0, q1, q2, q3} and ![]() ={a, b} and
={a, b} and ![]() = {a, b, $}
= {a, b, $}
Y las funciones de transición están dadas por:![]()
![]()
![]()
![]()
![]()
![]()

Veamos cómo funciona este autómata para aabb.
| Fila | Estado | Aporte | Función de transición | Cola (Entrada desde la izquierda) | Estado después del movimiento |
|---|---|---|---|---|---|
| 1 | q0 | un abb | δ(q0, a, ε)={(q0, a)} | a | q0 |
| 2 | q0 | un un bb | δ(q0, a, ε)={(q0, a)} | Automóvil club británico | q0 |
| 3 | q0 | ε | δ(q0, ε, ε)={(q1, $)} | $aaa | q1 |
| 4 | q1 | ε | δ(q1, ε, a)={(q2, ε)} | $a | q2 |
| 5 | q2 | ε | δ(q2, ε, a)={(q2, a)} | un $ | q2 |
| 6 | q2 | aa b b | δ(q2, b, $)={(q1, $)} | $a | q1 |
| 7 | q1 | ε | δ(q1, ε, a)={(q2, ε)} | ps | q2 |
| 8 | q2 | aab b | δ(q2, b, $)={(q1, $)} | ps | q1 |
| 9 | q1 | ε | δ(q1, ε, $)={(q3, $)} | ps | q3 |
Publicación traducida automáticamente
Artículo escrito por mayankjoshi0841 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA