PUERTA | PUERTA CS 2011 | Pregunta 33

Considere una secuencia finita de valores aleatorios X = { x ₁ , x ₂ ,…, x _n }. Sea μ _x la media y σ _x la desviación estándar de X . Dejemos que otra sucesión finita Y de igual longitud se derive de esto como y _i = a*x _i + b , donde a y b son constantes positivas. Sea μ _y la media y σ _ySea la desviación estándar de esta sucesión. ¿Cuál de las siguientes afirmaciones es INCORRECTA?
(A) La posición de índice del modo de X en X es la misma que la posición de índice del modo de Y en Y.
(B) La posición de índice de la mediana de X en X es la misma que la posición de índice de la mediana de Y en Y.
(C) μ _y = aμ _x +b
(D) σ _y = aσ _x +b

Respuesta: (D)
Explicación: Sumar una constante como b cambia la distribución mientras se multiplica a una constante como a estirar la distribución a lo largo de la mediana

La moda es el dato más frecuente de la distribución, por lo que la posición del índice de la moda no cambiará. Del gráfico anterior, está claro que la posición del índice de la mediana tampoco cambiará. Ahora para la media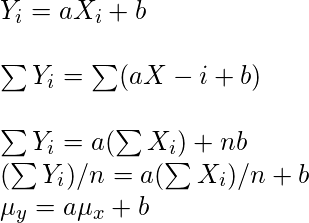
$Y_{i} = a X_{i} + b \newline \newline \sum Y_{i} = \sum(aX-{i} + b) \newline \sum Y_{i} = a(\sum X_{i}) + nb \newline (\sum Y_{i})/n = a(\sum X_{i})/n + b \newline \mu _{y} = a\mu_{x} + b$

Y para la desviación estándar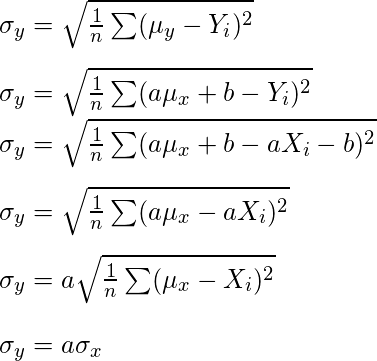
$\newline \newline \sigma _{y} = \sqrt{\frac{1}{n} \sum (\mu_{y} - Y_{i})^{2}} \newline \newline \sigma _{y} = \sqrt{\frac{1}{n} \sum (a\mu_{x} + b - Y_{i})^{2}} \newline \sigma _{y} = \sqrt{\frac{1}{n} \sum (a\mu_{x} + b - aX_{i} - b)^{2}} \newline \newline \sigma _{y} = \sqrt{\frac{1}{n} \sum (a\mu_{x} - aX_{i} )^{2}} \newline \newline \sigma _{y} = a\sqrt{\frac{1}{n} \sum (\mu_{x} - X_{i} )^{2}} \newline \newline \sigma _{y} = a\sigma_{x}$

Cuestionario de esta pregunta

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta