Dado un árbol de N Nodes y un número entero K , cada Node se numera entre 1 y N. La tarea es encontrar el número de pares de Nodes ideales en un árbol.
Un par de Nodes (a, b) se llama ideal si
- a es un antepasado de b .
- Y abs(a – b) ≤ K
Ejemplos:
Input:
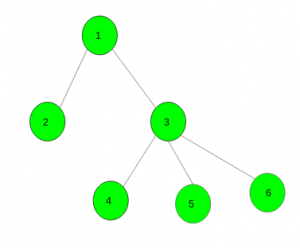
K = 2 Output: 4 (1, 2), (1, 3), (3, 4), (3, 5) are such pairs. Input: Consider the graph in example 1 and k = 3 Output: 6 (1, 2), (1, 3), (1, 4), (3, 4), (3, 5), (3, 6) are such pairs.
Enfoque: primero, necesitamos recorrer el árbol usando DFS , por lo que debemos encontrar el Node raíz, el Node sin un padre. A medida que atravesamos cada Node, lo almacenaremos en una estructura de datos para realizar un seguimiento de todos los ancestros del siguiente Node. Antes de hacer eso, obtenga el número de ancestros del Node en el rango [presentNode – k, presentNode + k] y luego agréguelo a los pares totales.
Necesitamos una estructura de datos que pueda:
- Inserte un Node a medida que atravesamos el árbol.
- Eliminar un Node a medida que regresamos.
- Proporcione el número de Nodes dentro del rango [presentNode – k, PresentNode + k] que se almacenaron.
El árbol indexado binario cumple las tres operaciones anteriores.
Podemos hacer las 3 operaciones anteriores inicializando todos los valores de índice del BIT a 0 y luego:
- Inserte un Node actualizando el índice de ese Node a 1.
- Elimina un Node actualizando el índice de ese Node a 0.
- Obtenga el número de pares similares del ancestro de ese Node consultando la suma del rango [presentNode – k, PresentNode + k]
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
#define N 100005
int n, k;
// Adjacency list
vector<int> al[N];
long long Ideal_pair;
long long bit[N];
bool root_node[N];
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
long long bit_q(int i, int j)
{
long long sum = 0ll;
while (j > 0) {
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0) {
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
void bit_up(int i, long long diff)
{
while (i <= n) {
bit[i] += diff;
i += i & -i;
}
}
// DFS function to find ideal pairs
void dfs(int node)
{
Ideal_pair += bit_q(max(1, node - k),
min(n, node + k));
bit_up(node, 1);
for (int i = 0; i < al[node].size(); i++)
dfs(al[node][i]);
bit_up(node, -1);
}
// Function for initialisation
void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0LL;
}
}
// Function to add an edge
void Add_Edge(int x, int y)
{
al[x].push_back(y);
root_node[y] = false;
}
// Function to find number of ideal pairs
long long Idealpairs()
{
// Find root of the tree
int r = -1;
for (int i = 1; i <= n; i++)
if (root_node[i]) {
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
// Driver code
int main()
{
n = 6, k = 3;
initialise();
// Add edges
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
// Function call
cout << Idealpairs();
return 0;
}
Java
// Java implementation of the approach
import java.util.*;
class GFG{
static final int N = 100005;
static int n, k;
// Adjacency list
@SuppressWarnings("unchecked")
static Vector<Integer> []al = new Vector[N];
static long Ideal_pair;
static long []bit = new long[N];
static boolean []root_node = new boolean[N];
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
static long bit_q(int i, int j)
{
long sum = 0;
while (j > 0)
{
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0)
{
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
static void bit_up(int i, long diff)
{
while (i <= n)
{
bit[i] += diff;
i += i & -i;
}
}
// DFS function to find ideal pairs
static void dfs(int node)
{
Ideal_pair += bit_q(Math.max(1, node - k),
Math.min(n, node + k));
bit_up(node, 1);
for(int i = 0; i < al[node].size(); i++)
dfs(al[node].get(i));
bit_up(node, -1);
}
// Function for initialisation
static void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0;
}
}
// Function to add an edge
static void Add_Edge(int x, int y)
{
al[x].add(y);
root_node[y] = false;
}
// Function to find number of ideal pairs
static long Idealpairs()
{
// Find root of the tree
int r = -1;
for(int i = 1; i <= n; i++)
if (root_node[i])
{
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
// Driver code
public static void main(String[] args)
{
n = 6;
k = 3;
for(int i = 0; i < al.length; i++)
al[i] = new Vector<Integer>();
initialise();
// Add edges
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
// Function call
System.out.print(Idealpairs());
}
}
// This code is contributed by Amit Katiyar
Python3
# Python3 implementation of the approach N = 100005 Ideal_pair = 0 # Adjacency list al = [[] for i in range(100005)] bit = [0 for i in range(N)] root_node = [0 for i in range(N)] # bit : bit array # i and j are starting and # ending index INCLUSIVE def bit_q(i, j): sum = 0 while (j > 0): sum += bit[j] j -= (j & (j * -1)) i -= 1 while (i > 0): sum -= bit[i] i -= (i & (i * -1)) return sum # bit : bit array # n : size of bit array # i is the index to be updated # diff is (new_val - old_val) def bit_up(i, diff): while (i <= n): bit[i] += diff i += i & -i # DFS function to find ideal pairs def dfs(node, x): Ideal_pair = x Ideal_pair += bit_q(max(1, node - k), min(n, node + k)) bit_up(node, 1) for i in range(len(al[node])): Ideal_pair = dfs(al[node][i], Ideal_pair) bit_up(node, -1) return Ideal_pair # Function for initialisation def initialise(): Ideal_pair = 0; for i in range(n + 1): root_node[i] = True bit[i] = 0 # Function to add an edge def Add_Edge(x, y): al[x].append(y) root_node[y] = False # Function to find number of ideal pairs def Idealpairs(): # Find root of the tree r = -1 for i in range(1, n + 1, 1): if (root_node[i]): r = i break Ideal_pair = dfs(r, 0) return Ideal_pair # Driver code if __name__ == '__main__': n = 6 k = 3 initialise() # Add edges Add_Edge(1, 2) Add_Edge(1, 3) Add_Edge(3, 4) Add_Edge(3, 5) Add_Edge(3, 6) # Function call print(Idealpairs()) # This code is contributed by # Surendra_Gangwar
C#
// C# implementation of the
// above approach
using System;
using System.Collections.Generic;
class GFG{
static readonly int N = 100005;
static int n, k;
// Adjacency list
static List<int> []al =
new List<int>[N];
static long Ideal_pair;
static long []bit =
new long[N];
static bool []root_node =
new bool[N];
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
static long bit_q(int i,
int j)
{
long sum = 0;
while (j > 0)
{
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0)
{
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
static void bit_up(int i,
long diff)
{
while (i <= n)
{
bit[i] += diff;
i += i & -i;
}
}
// DFS function to find
// ideal pairs
static void dfs(int node)
{
Ideal_pair += bit_q(Math.Max(1,
node - k),
Math.Min(n,
node + k));
bit_up(node, 1);
for(int i = 0;
i < al[node].Count; i++)
dfs(al[node][i]);
bit_up(node, -1);
}
// Function for
// initialisation
static void initialise()
{
Ideal_pair = 0;
for (int i = 0; i <= n; i++)
{
root_node[i] = true;
bit[i] = 0;
}
}
// Function to add an edge
static void Add_Edge(int x,
int y)
{
al[x].Add(y);
root_node[y] = false;
}
// Function to find number
// of ideal pairs
static long Idealpairs()
{
// Find root of the tree
int r = -1;
for(int i = 1; i <= n; i++)
if (root_node[i])
{
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
// Driver code
public static void Main(String[] args)
{
n = 6;
k = 3;
for(int i = 0; i < al.Length; i++)
al[i] = new List<int>();
initialise();
// Add edges
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
// Function call
Console.Write(Idealpairs());
}
}
// This code is contributed by Amit Katiyar
Javascript
<script>
// Javascript implementation of the approach
let N = 100005;
let n, k;
// Adjacency list
let al = new Array(N).fill(0).map((t) => []);
let Ideal_pair;
let bit = new Array(N);
let root_node = new Array(N);
// bit : bit array
// i and j are starting and
// ending index INCLUSIVE
function bit_q(i, j) {
let sum = 0;
while (j > 0) {
sum += bit[j];
j -= (j & (j * -1));
}
i--;
while (i > 0) {
sum -= bit[i];
i -= (i & (i * -1));
}
return sum;
}
// bit : bit array
// n : size of bit array
// i is the index to be updated
// diff is (new_val - old_val)
function bit_up(i, diff) {
while (i <= n) {
bit[i] += diff;
i += i & -i;
}
}
// DFS function to find ideal pairs
function dfs(node) {
Ideal_pair += bit_q(Math.max(1, node - k),
Math.min(n, node + k));
bit_up(node, 1);
for (let i = 0; i < al[node].length; i++)
dfs(al[node][i]);
bit_up(node, -1);
}
// Function for initialisation
function initialise() {
Ideal_pair = 0;
for (let i = 0; i <= n; i++) {
root_node[i] = true;
bit[i] = 0;
}
}
// Function to add an edge
function Add_Edge(x, y) {
al[x].push(y);
root_node[y] = false;
}
// Function to find number of ideal pairs
function Idealpairs() {
// Find root of the tree
let r = -1;
for (let i = 1; i <= n; i++)
if (root_node[i]) {
r = i;
break;
}
dfs(r);
return Ideal_pair;
}
// Driver code
n = 6, k = 3;
initialise();
// Add edges
Add_Edge(1, 2);
Add_Edge(1, 3);
Add_Edge(3, 4);
Add_Edge(3, 5);
Add_Edge(3, 6);
// Function call
document.write(Idealpairs());
// This code is contributed by _saurabh_jaiswal
</script>
6
Complejidad de tiempo: O(N*log(N))
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA