Serie Maclaurin – Barcelona Geeks

Requisito previo: teorema de Taylor y serie de Taylor

Sabemos que la fórmula para la expansión de la serie de Taylor se escribe como:
$f(x)=f(a)+\sum_{n=1}^{\infty}\frac{f^n(a)}{n!}(xa)^n$

Ahora bien, si ponemos a=0 en esta fórmula, obtendremos la fórmula para la expansión de la serie de Maclaurin. Por lo tanto, la
expansión en serie de Maclaurin se puede dar mediante la fórmula:
$f(x)=f(0)+\sum_{n=1}^{\infty}\frac{f^n(0)}{n!}(x)^n$

Expansión en serie de Maclaurin de algunas funciones elementales:

Función exponencial:
$f(x)=e^x$
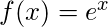
Derivando n veces,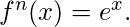 $f^n(x)=e^x.$
entonces obtenemos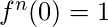 $f^n(0)=1$
Así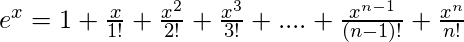 $e^x = 1+\frac{x}{1!}+ \frac{x^2}{2!}+ \frac{x^3}{3!}+....+ \frac{x^{n-1}}{(n-1)!}+\frac{x^n}{n!}$
f(x) = cos x
$\cosx= 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+$ …..
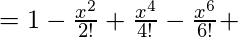f(x) = sen x
$\sinx = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+....$
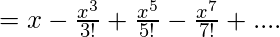
f(x) = (ax + b)^m
$(ax+b)^m=b^m[1+m(a/b)\frac{x}{1!}+m(m-1)(a/b)^2\frac{x^2}{2!}+m(m-1)(m-2)(a/b)^3\frac{x^3}{3!}+.....$
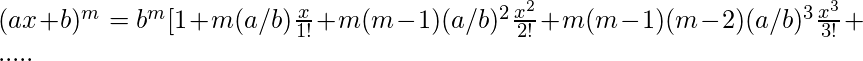
f(x) = ln(1+x)
$\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}+.....+(-1)^{n-1}\frac{x^n}{n}+.....$
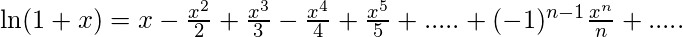
f(x) = ln(1-x)
$\ln(1-x)=-(x+\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{x^5}{5}+.....+\frac{x^n}{n}+....)$

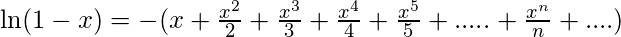
Ejemplo-1:
Encuentra los primeros siete términos de f(x) = ln(sec x).

Explicación:
$f(x) = ln(\secx)$
$f(0) = ln(\sec0)=0$
Al diferenciar wrt x,
$f'(x)= (1/secx).\secx.\tanx = \tan x$
$f'(0)= \tan 0 = 0$
$f''(x)= \sec^2x\scriptstyle\implies f''(0) = \sec^20=1$
$f'''(x)= 2\secx.\secx.\tanx=2sec^2x.tanx\scriptstyle\implies f'''(0) = 0$
$f''''(x)= 4\sec^2x.\tan^2x+2\sec^4x\scriptstyle\implies f''''(0) = 0+2 = 2$
$f'''''(x)= 8\sec^2x.\tan^3x+16\sec4x.\tanx\scriptstyle\implies f'''''(0) = 0$
$f''''''(x)= 16\sec^2x.\tan^4x+88\sec4x.\tan^2x+16\sec^6x\scriptstyle\implies f''''''(0) = 16$
obtenemos la serie de Maclaurin como:
$f(x) = f(0)+f'(0).x/1!+f''(0).x^2/2!+f'''(0).x^3/3!+.... \text{upto 7 terms}$
$f(x)=ln(\secx)=0+1.x^2/2!+0+2.x^4/4!+0+16x^6/6!+....$
$f(x)=\frac{x^2}{2}+\frac{x^4}{12}+\frac{x^6}{45}+....$

Ejemplo-2:
Evalúe la serie de Maclaurin para tan x.

Explicación:
$f(x) = \tan x, f(0)=0$
$f'(x) = \sec^2x \scriptstyle\implies f'(0)=1$
$f''(x) = 2\sec^x.\secx.\tanx=2\sec^2x.\tanx=2(\tanx+\tan^3x) \scriptstyle\implies f''(0)=0$
$f'''(x) = 2+8\tan^2x+6\tan^4x \scriptstyle\implies f'''(0)=2$
$f''''(x) = 16\tanx+40\tan^3x+24\tan^5x \scriptstyle\implies f''''(0)=0$
$f'''''(x) = 16\sec^2x+120\tan^2x.sec^2x+120\tan^4x\sec^2x \scriptstyle\implies f'''''(0)=16$
Por lo tanto, obtenemos la serie de Maclaurin como:
$\tanx=x+\frac{1}{3}x^3+\frac{2}{15}x^5+.......$

Publicación traducida automáticamente

Artículo escrito por mohitg593 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta