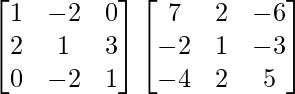
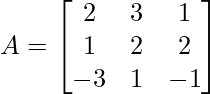
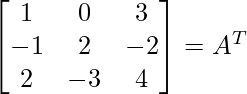
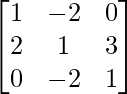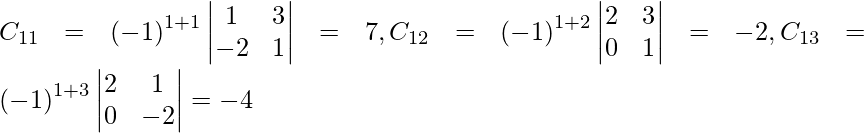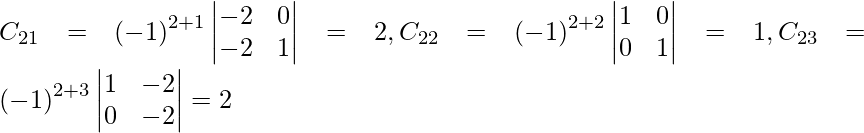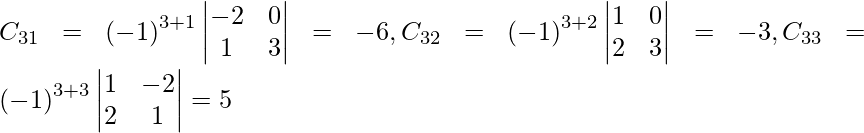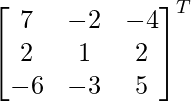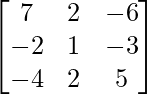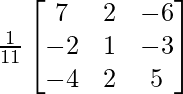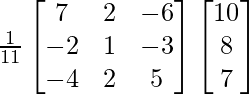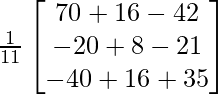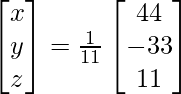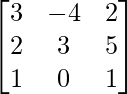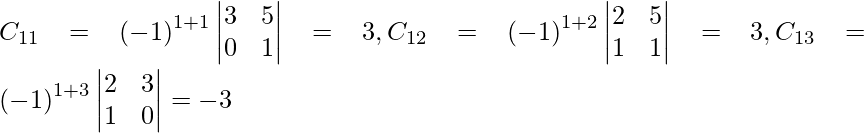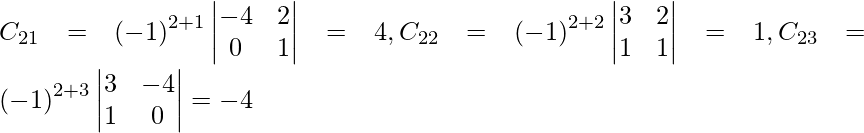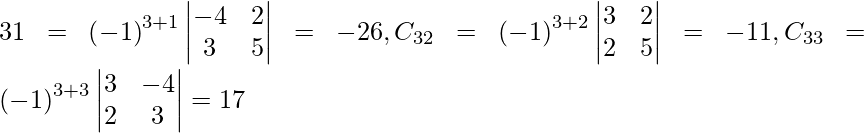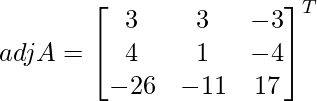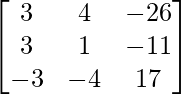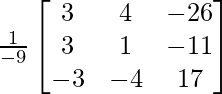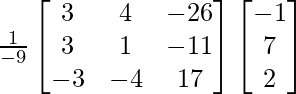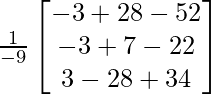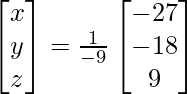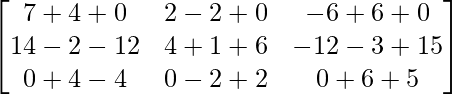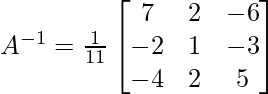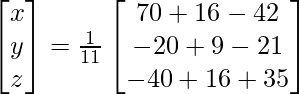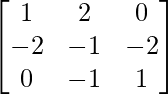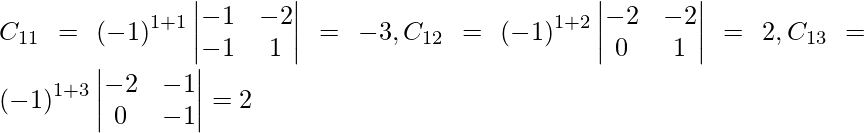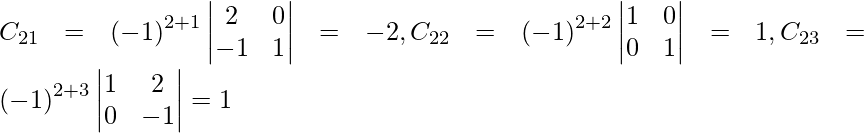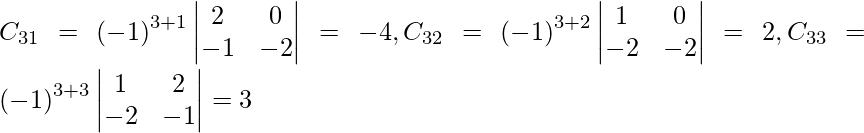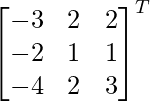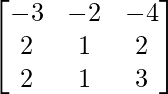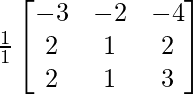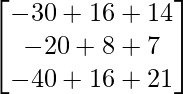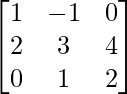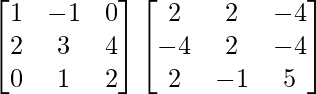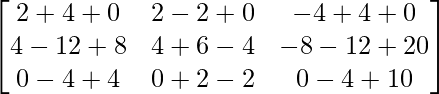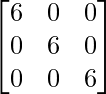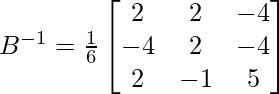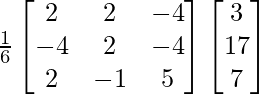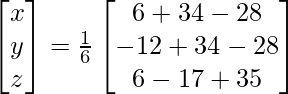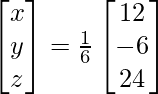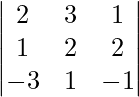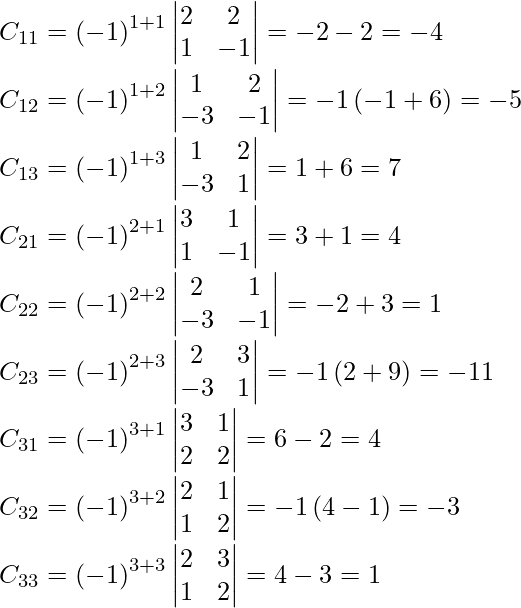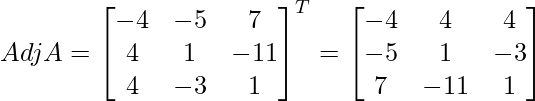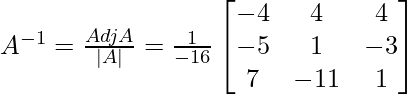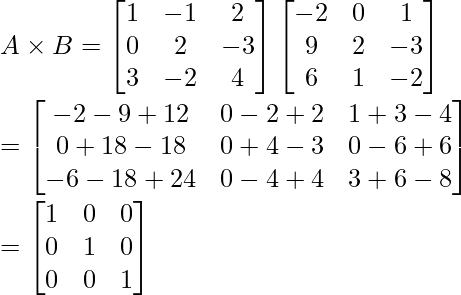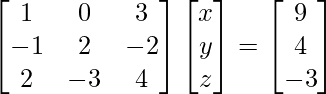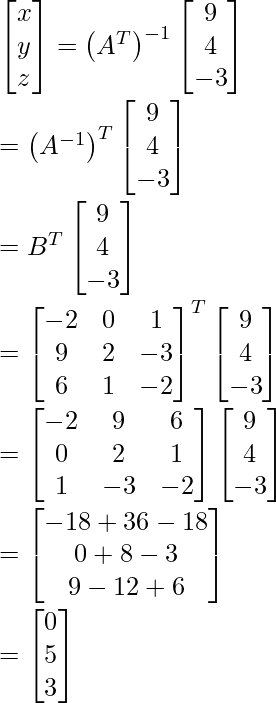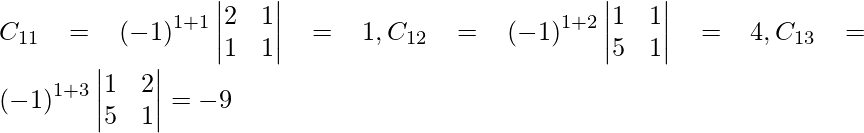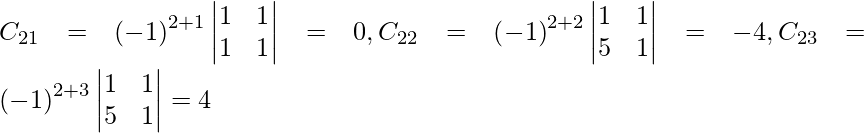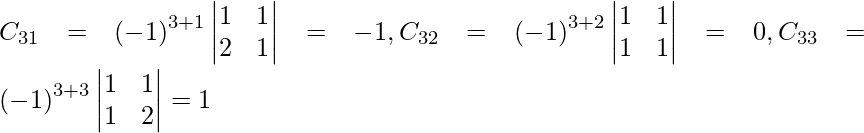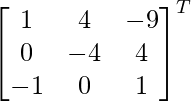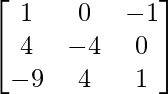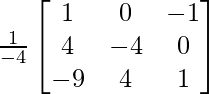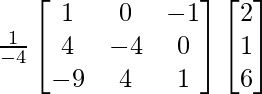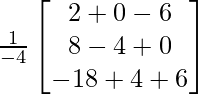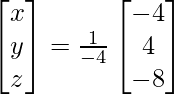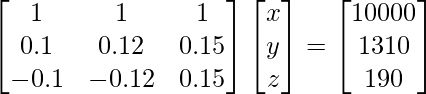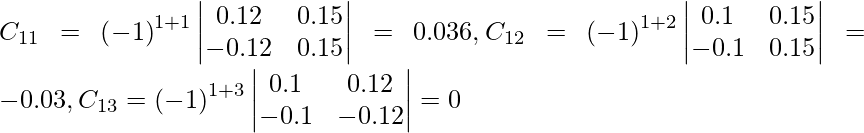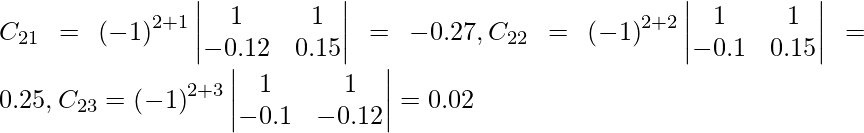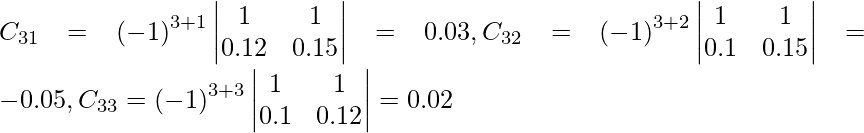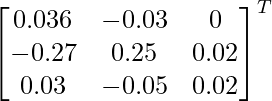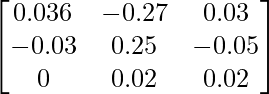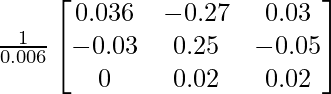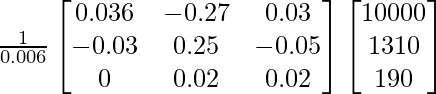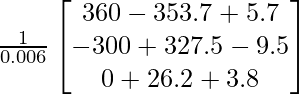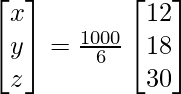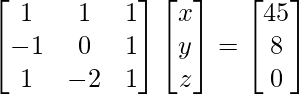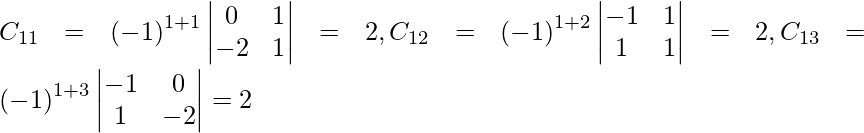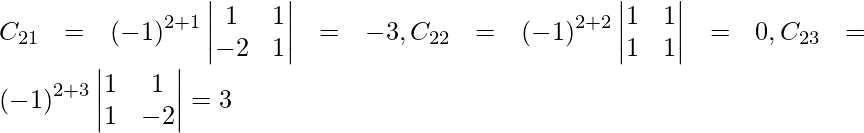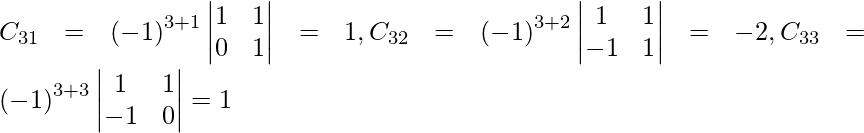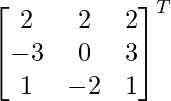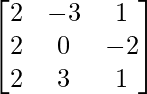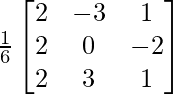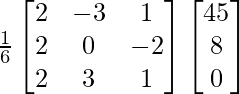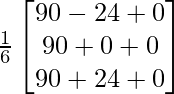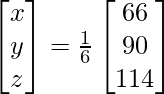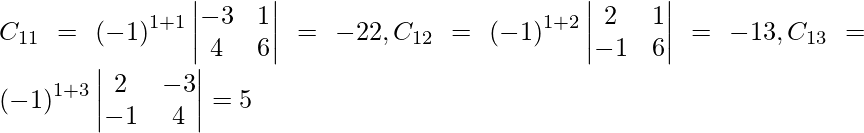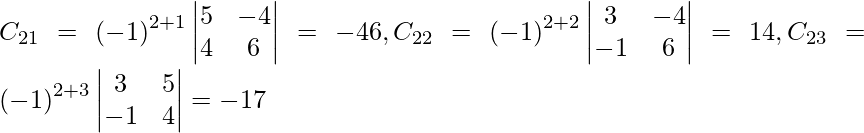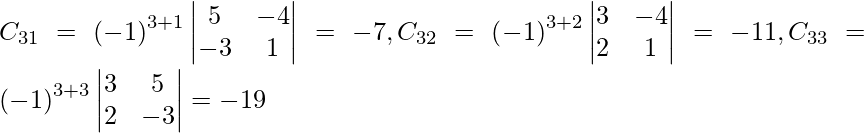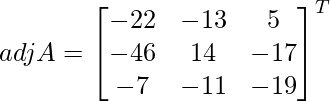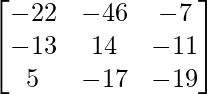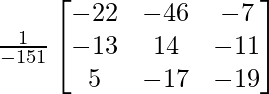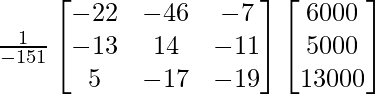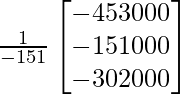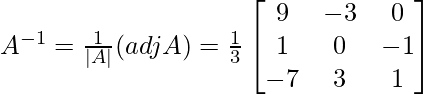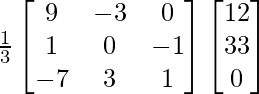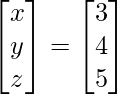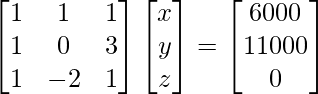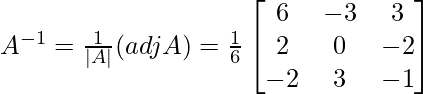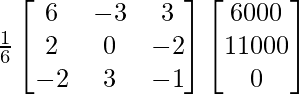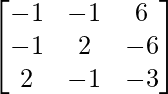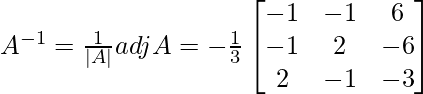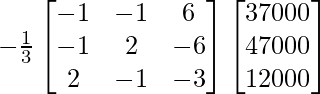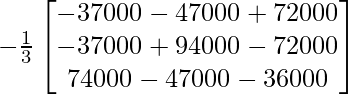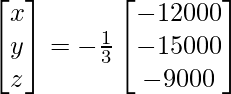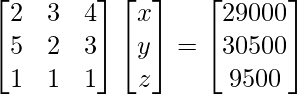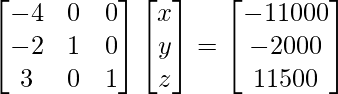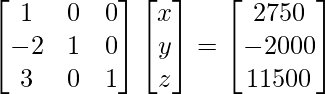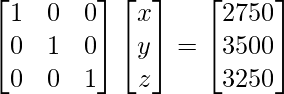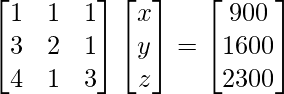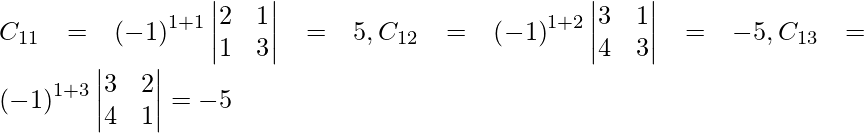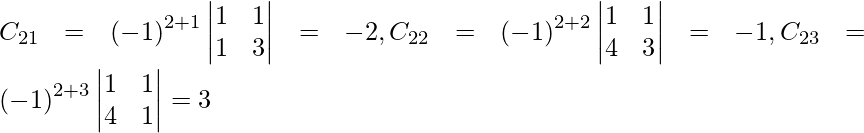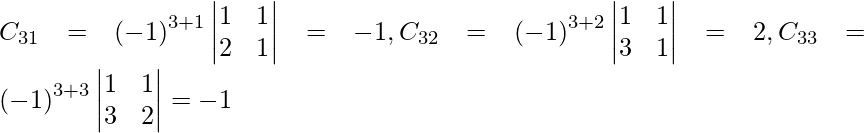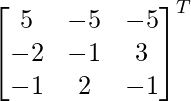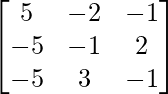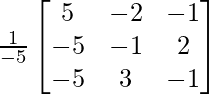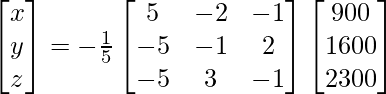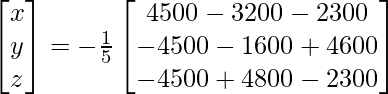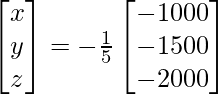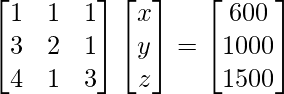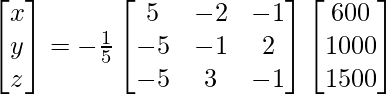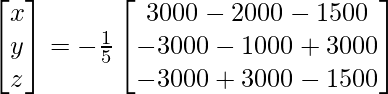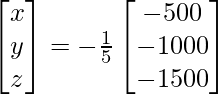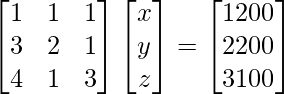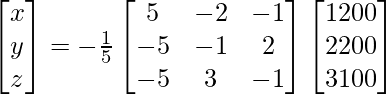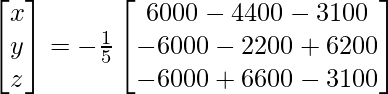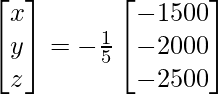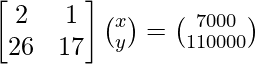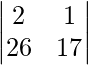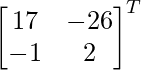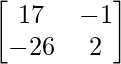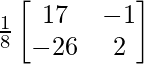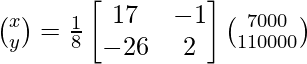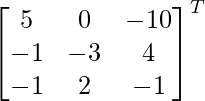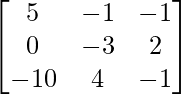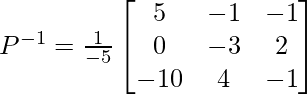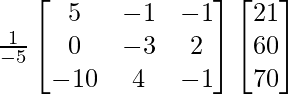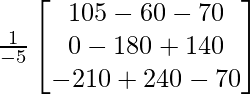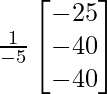Pregunta 8. (i) Si A = 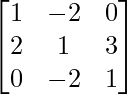 , encuentre A −1 . Usando A −1 , resuelve el sistema de ecuaciones lineales x − 2y = 10, 2x + y + 3z = 8, −2y + z = 7.
, encuentre A −1 . Usando A −1 , resuelve el sistema de ecuaciones lineales x − 2y = 10, 2x + y + 3z = 8, −2y + z = 7.
Solución:
Aquí,
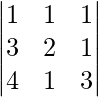
un =
|A| = 1 (1 + 6) + 2 (2 – 0) + 0 (- 4 – 0)
= 7 + 4 + 0
= 11
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
Ahora, X = A -1 B
X =
X =
Por lo tanto x = 4, y = -3 y z = 1.
(ii) Si A = 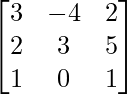 , encuentre A −1 y, por lo tanto, resuelva el siguiente sistema de ecuaciones:
, encuentre A −1 y, por lo tanto, resuelva el siguiente sistema de ecuaciones:
Solución:
Aquí,
un =
|A| = 9 – 12 – 6
= -9
Sean C ij los cofactores de los elementos a ij en A.
=
un =
Aquí,
A =
, X =
y B =
X = A -1B
X =
X =
Por lo tanto x = 3, y = 2 y z = – 1.
(iii) Si A = 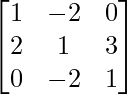 y B =
y B = 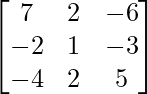 , encuentre AB. Por tanto, resuelve el sistema de ecuaciones: x − 2y = 10, 2x + y + 3z = 8 y −2y + z = 7.
, encuentre AB. Por tanto, resuelve el sistema de ecuaciones: x − 2y = 10, 2x + y + 3z = 8 y −2y + z = 7.
Solución:
Aquí,
A =
, B =
AB =
=
=
=
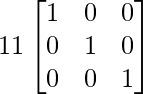
= 11 yo
=>
X = A -1B
X =
Por lo tanto x = 4, y = -3 y z = 1.
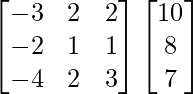
(iv) Si A = 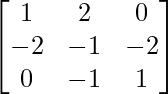 , encuentre A −1 . Usando A −1 , resuelve el sistema de ecuaciones lineales: x − 2y = 10, 2x − y − z = 8, −2y + z = 7.
, encuentre A −1 . Usando A −1 , resuelve el sistema de ecuaciones lineales: x − 2y = 10, 2x − y − z = 8, −2y + z = 7.
Solución:
Aquí,
un =
|A| = -3 + 4 + 0
= 1
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
=
Ahora, X = A -1 B
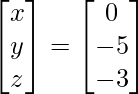
X =
X =
Por lo tanto x = 0, y = – 5 y z = -3.
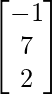
(v) Si A = 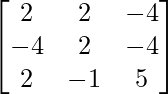 , B =
, B = 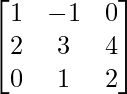 , encuentre BA y use esto para resolver el sistema de ecuaciones y + 2z = 7, x − y = 3, 2x + 3y + 4z = 17.
, encuentre BA y use esto para resolver el sistema de ecuaciones y + 2z = 7, x − y = 3, 2x + 3y + 4z = 17.
Solución:
Tenemos,
A =
, B =
AB =
AB =
AB =
AB =
AB = 6I
Ahora, BX = C. Entonces, tenemos
X = B -1C
X =
Por lo tanto x = 2, y = – 1 y z = 4.
(vi) Si 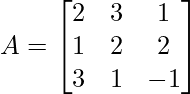 , encuentre A –1 y, por lo tanto, resuelva el sistema de ecuaciones 2x + y – 3z = 13, 3x + 2y + z = 4, x + 2y – z = 8.
, encuentre A –1 y, por lo tanto, resuelva el sistema de ecuaciones 2x + y – 3z = 13, 3x + 2y + z = 4, x + 2y – z = 8.
Solución:
Tenemos,
|A| =
= 2 (-2 – 2) – 3 (-1 + 6) + 1(1 + 6)
= -8 – 15 + 7
= -16 ≠ 0
Por lo tanto, A es invertible.
Calcule los cofactores para encontrar la array adjunta.
Entonces obtenemos,
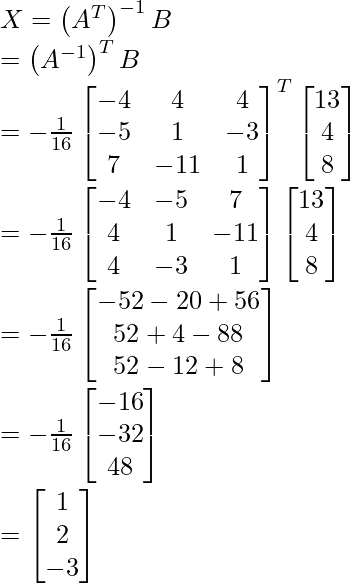
X =
, B =
Por tanto, el sistema de ecuaciones dado tiene solución única.
Por lo tanto, x = 1, y = 2 y z = −3.
(vii) Use el producto 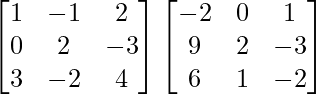 para resolver el sistema de ecuaciones x + 3z = 9, −x + 2y − 2z = 4, 2x − 3y + 4z = −3.
para resolver el sistema de ecuaciones x + 3z = 9, −x + 2y − 2z = 4, 2x − 3y + 4z = −3.
Solución:
Tenemos,
Aquí,
Como A × B = I, tenemos B = A −1
Aquí, el sistema de ecuaciones dado es,
x + 3z = 9
−x + 2y − 2z = 4
2x − 3y + 4z = −3
Entonces obtenemos,
Aquí,
Por eso,
Entonces obtenemos,
Por lo tanto, x = 0, y = 5 y z = 3.
Pregunta 9. La suma de tres números es 2. Si a la suma del primero y el tercero se le suma el doble del segundo número, la suma es 1. Al sumar el segundo y el tercer número cinco veces el primero, obtenemos 6. Encuentra los tres números usando arrays.
Solución:
Sean los tres números x, y y z.
Según la pregunta,
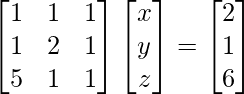
x + y + z = 2
x + 2y + z = 1
5x + y + z = 6
El sistema de ecuaciones dado se puede escribir en forma matricial como,
A =
, X =
y B =
|A| = 1 + 4 – 9
= -4
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
X = A -1B
X =
X =
Por lo tanto x = 1, y = – 1 y z = 2.
Pregunta 10. Se coloca una cantidad de 10.000 rupias en tres inversiones a una tasa de 10, 12 y 15% anual. El ingreso combinado es de 1310 rupias y el ingreso combinado de la primera y la segunda inversión es de 190 rupias, por debajo de los ingresos de la tercera. Encuentre la inversión en cada uno utilizando el método matricial.
Solución:
Sean los números x, y, y z.
x + y + z = 10,000
0,1x + 0,12y + 0,15z = 1310
0,1x + 0,12y – 0,15z = – 190
El sistema de ecuaciones dado se puede escribir en forma matricial como,
Aquí,
A =
, X =
y B =
|A| = 0,036 – 0,03 + 0
= 0,006
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
X = A -1B
X =
X =
Por lo tanto x = 2000, y = 3000 y z = 5000.
Así, las tres inversiones son de Rs 2000, Rs 3000 y Rs 5000, respectivamente.
Pregunta 11. Una empresa produce tres productos todos los días. Su producción en un día determinado es de 45 toneladas. Se encuentra que la producción del tercer producto excede la producción del primer producto en 8 toneladas mientras que la producción total del primer y tercer producto es el doble de la producción del segundo producto. Determinar el nivel de producción de cada producto utilizando el método matricial.
Solución:
Sean x, y y z el nivel de producción del primer, segundo y tercer producto, respectivamente.
x + y + z = 45
– x + z = 8
x – 2y + z = 0
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
A =
, X =
, B =
Ahora,
|A| = 2 + 2 + 2
= 6
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
X = A -1B
X =
X =
Por lo tanto x = 11, y = 15 y z = 19.
Así, el nivel de producción del primer, segundo y tercer producto es 11, 15 y 19, respectivamente.
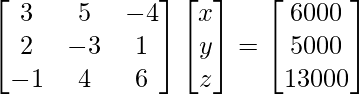
Pregunta 12. Los precios de tres mercancías P, Q y R son Rs x, y y z por unidad respectivamente. A compra 4 unidades de R y vende 3 unidades de P y 5 unidades de Q. B compra 3 unidades de Q y vende 2 unidades de P y 1 unidad de R. C compra 1 unidad de P y vende 4 unidades de Q y 6 unidades de R. En el proceso, A, B y C ganan Rs 6000, Rs 5000 y Rs 13000 respectivamente. Si vender las unidades es una ganancia positiva y comprar las unidades es una ganancia negativa, encuentre el precio por unidad de tres productos utilizando el método matricial.
Solución:
Los precios de tres mercancías P, Q y R son Rs x, Rs y y Rs z por unidad, respectivamente.
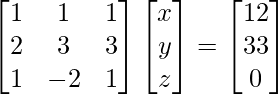
3x + 5y – 4z = 6000
2x – 3y + z = 5000
-x + 4y + 6z = 13000
El sistema de ecuaciones dado se puede escribir en forma matricial de la siguiente manera:
AX = B
Aquí,
A =
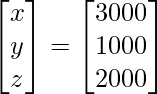
, X =
, B =
Ahora,
|A| = -66 – 65 – 20
= -151
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
X =
X =
Por lo tanto x = 3000, y = 1000 y z = 2000.
Por lo tanto, los precios de los tres productos P, Q y R son Rs 3000, Rs 1000 y Rs 2000 por unidad, respectivamente.
Pregunta 13. El comité de administración de una colonia residencial decidió premiar a algunos de sus miembros (digamos x) por su honestidad, algunos (digamos y) por ayudar a los demás y algunos otros (digamos z) por supervisar a los trabajadores para mantener la colonia limpia y ordenada. limpio. La suma de todos los premiados es 12. Tres veces la suma de premiados por cooperación y supervisión más dos veces el número de premiados por honestidad es 33. Si la suma del número de premiados por honestidad y supervisión es el doble del número de premiados para ayudar a otros, usando el método matricial, encuentre el número de premiados de cada categoría. Aparte de estos valores, a saber, la honestidad, la cooperación y la supervisión, sugieren un valor más que la gestión de la colonia debe incluir para los premios.
Solución:
De acuerdo con la pregunta, tenemos
x + y + z = 12
2x + 3(y +z) = 33
x + z -2y = 0
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
A =
, X =
y B =
Ahora, |A| = 3.
Y adj A viene dado por
.
X = A -1B
X =
Por lo tanto x= 3, y = 4 y z = 5.
Por lo tanto, el número de premiados por Honestidad, Cooperación y Supervisión son 3, 4 y 5 respectivamente.
Un valor más que la gestión de la colonia debe incluir en los premios puede ser la Sinceridad.
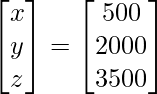
Pregunta 14. Una escuela quiere premiar a sus estudiantes por los valores de Honestidad, Regularidad y Trabajo Duro con un premio total en efectivo de Rs 6,000. Tres veces el dinero del premio por el trabajo duro sumado al otorgado por la honestidad asciende a 11.000 rupias. El dinero del premio otorgado por la Honestidad y el Trabajo Duro juntos es el doble del otorgado por la Regularidad. Represente la situación anterior algebraicamente y encuentre el premio en dinero para cada valor, utilizando el método matricial. Aparte de estos valores, a saber, Honestidad, Regularidad y Trabajo duro, sugiera un valor más que la escuela debe incluir para los premios.
Solución:
Sea x, y y z respectivamente el dinero del premio otorgado por Honestidad, Regularidad y Trabajo duro.
x + y + z = 6000
x + 3 z = 11,000
x − 2y + z = 0
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí, A =
, X =
y B =
Ahora, |A| = 6.
Y adj A viene dado por
.
X = A -1B
X =
Por lo tanto x = 500, y = 2000 y z = 3500.
Por lo tanto, el dinero del premio otorgado por Honestidad, Regularidad y Trabajo duro es de 500 rupias, 2000 rupias y 3500 rupias, respectivamente.
La escuela puede incluir la sinceridad para los premios.
Pregunta 15. Dos instituciones decidieron premiar a sus empleados por los tres valores de ingenio, competencia y determinación en forma de precios a razón de Rs. x, y y z respectivamente por persona. La primera institución decidió premiar respectivamente a 4, 3 y 2 empleados con un precio total en efectivo de Rs. 37000 y la segunda institución decidió premiar respectivamente a 5, 3 y 4 empleados con un precio total en efectivo de Rs. 47000. Si los tres precios por persona juntos ascienden a Rs. 12000 luego, utilizando el método de array, encuentre el valor de x, y y z.
Solución:
De acuerdo con la pregunta, tenemos
4x + 3y + 2z = 37000
5x + 3y + 4z = 47000
x + y + z = 12000
Podemos expresar estas ecuaciones como AX = B donde, A =
, X =
y B =
|A| = 4 (3 – 4) – 3 (5 – 4) + 2 (5 – 3)
= -4 – 3 + 4
= -3
adj A =
X = A -1B
X =
X =
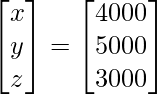
Entonces, x = 4000, y = 5000 y z = 3000.
Pregunta 16. Dos fábricas decidieron otorgar a sus empleados tres valores de (a) adaptables a nuevas técnicas, (b) cuidadosos y alertas en situaciones difíciles, y (c) manteniendo la calma en situaciones tensas, a razón de ₹ x, ₹ y , y ₹ z por persona respectivamente. La primera fábrica decidió honrar respectivamente a 2, 4 y 3 empleados con un premio en metálico total de ₹ 29 000. La segunda fábrica decidió honrar respectivamente a 5, 2 y 3 empleados con un premio en metálico de ₹ 30 500. Si los tres premios por persona juntos cuestan ₹ 9500, entonces
(i) represente la situación anterior mediante una ecuación matricial y forme una ecuación lineal usando la multiplicación matricial.
(ii) Resuelva estas ecuaciones por el método matricial.
Solución:
Según pregunta,
2x + 3y + 4z = 29000
5x + 2y + 3z = 30500
x + y + z = 9500
El sistema de ecuaciones dado se puede escribir en forma matricial como,
Por lo tanto x = 2750, y = 3500 y z = 3250.
Pregunta 17. Dos escuelas A y B quieren premiar a sus estudiantes seleccionados con los valores de sinceridad, veracidad y utilidad. La escuela A quiere otorgar ₹x a cada uno, ₹y a cada uno y ₹z a cada uno por los tres valores respectivos a 3, 2 y 1 estudiante respectivamente, con un premio total de 1600 ₹. La escuela B quiere gastar ₹ 2300 para premiar a sus 4, 1 y 3 estudiantes en los valores respectivos (dando el mismo dinero de premio a los tres valores que antes). Si el monto total de la adjudicación de un premio en cada valor es ₹ 900, usando arrays, encuentre el dinero de la adjudicación para cada valor. Además de estos tres valores, sugiera un valor más que debería considerarse para la adjudicación.
Solución:
Deje que el dinero del premio otorgado por sinceridad, veracidad y ayuda sea ₹x, ₹y y ₹z respectivamente.
x + y + z = 900
3x + 2y + z = 1600
4x + y + 3z = 2300
El sistema de ecuaciones anterior se puede escribir en forma matricial como,
, donde C =
, X =
y D =
Ahora, |C| =
= 5 – 5 – 5
= -5
Sean C ij los cofactores de los elementos a ij en A.
adj C =
=
=
X = C -1 D
Por lo tanto, x = -1000/-5, y = -1500/- 5 y z = -2000/-5
Entonces, x = 200, y = 300 y z = 400.
Por lo tanto, el dinero del premio por cada valor de sinceridad, veracidad y utilidad es ₹ 200, ₹ 300 y ₹ 400.
Un valor más que debe tenerse en cuenta para premiar el trabajo duro.
Pregunta 18. Dos escuelas P y Q quieren premiar a sus estudiantes seleccionados en los valores de Disciplina, Cortesía y Puntualidad. La escuela P quiere otorgar ₹x a cada uno, ₹y a cada uno y ₹z a cada uno de los tres valores respectivamente a sus 3, 2 y 1 estudiantes con un premio total de 1000 ₹. La escuela Q quiere gastar ₹ 1500 para premiar a sus 4, 1 y 3 estudiantes en los valores respectivos (dando el mismo dinero de premio para tres valores que antes). Si la cantidad total de premios para un premio en cada valor es ₹ 600, usando arrays, encuentre el dinero del premio para cada valor. Además de los tres valores anteriores, sugiera un valor más para los premios.
Solución:
Deje que el dinero del premio otorgado por Disciplina, Cortesía y Puntualidad sea ₹x, ₹y y ₹z respectivamente.
x + y + z = 600
3x + 2y + z = 1000
4x + y + 3z = 1500
El sistema de ecuaciones anterior se puede escribir en forma matricial AX = B como
Aquí, A =
, X =
y B =
Ahora,
|A| =
= 5 – 5 – 5
= -5
adj A =
=
=
X = A -1B
=> x = -500/- 5, y = -1000/- 5 y z = -1500/- 5
Por lo tanto x = 100, y = 200 y z = 300.
Por lo tanto, el dinero del premio por cada valor de Disciplina, Cortesía y Puntualidad es ₹ 100, ₹ 200 y ₹ 300.
Un valor más que debe ser considerado para el premio es la Honestidad.
Pregunta 19. Dos escuelas P y Q quieren premiar a sus estudiantes seleccionados por los valores de Tolerancia, Bondad y Liderazgo. La escuela P quiere otorgar ₹x cada uno, ₹y cada uno y ₹z cada uno por los tres valores respectivos a 3, 2 y 1 estudiante respectivamente con un premio total en dinero de ₹2200. La escuela Q quiere gastar ₹ 3100 para premiar a sus 4, 1 y 3 estudiantes en los valores respectivos (dando el mismo dinero de premio a los tres valores que la escuela P). Si el monto total de la adjudicación de un premio en cada valor es ₹ 1200, usando arrays, encuentre el dinero de la adjudicación para cada valor.
Además de estos tres valores, sugiera un valor más que debería considerarse para la adjudicación.
Solución:
Deje que el dinero del premio otorgado por Tolerancia, Bondad y Liderazgo sea ₹x, ₹y y ₹z respectivamente.
x + y + z = 1200
3x + 2y + z = 2200
4x + y + 3z = 3100
El sistema de ecuaciones anterior se puede escribir en forma matricial AX = B como
donde, A =
, X =
y B =
Ahora,
|A| =
= 5 – 5 – 5
= -5
adj A =
=
=
X = A -1B
=> x = – 1500/-5, y = – 2000/-5 y z = -2500/-5
Por lo tanto x = 300, y = 400 y z = 500.
Por lo tanto, el dinero del premio para cada valor de Tolerancia, Amabilidad y Liderazgo es de 300 rupias, 400 rupias y 500 rupias.
Un valor más que debe ser considerado para el premio es la Honestidad.
Pregunta 20. Se deposita un monto total de ₹ 7000 en tres cuentas bancarias de ahorro diferentes con tasas de interés anuales del 5 %, 8 % y 8,5 %, respectivamente. El interés anual total de estas tres cuentas es de ₹ 550. Se han depositado cantidades iguales en las cuentas de ahorro al 5% y al 8%. Encuentra la cantidad depositada en cada una de las tres cuentas, con la ayuda de arrays.
Solución:
Sea la cantidad depositada en cada una de las tres cuentas $x, $x y $y respectivamente.
2x + y = 7000
26x + 17y = 110000
El sistema de ecuaciones anterior se puede escribir en forma matricial AX = B como,
donde, A =
, X =
y B =
Ahora,
|A| =
= 34 – 26
= 8
adj A =
=
=
X = A -1B
=> x =
y y =
Por lo tanto x = 1125 y y = 4750.
Por lo tanto, la cantidad depositada en cada una de las tres cuentas es ₹ 1125, ₹ 1125 y ₹ 4750.
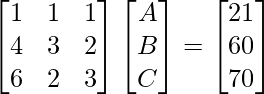
Pregunta 21. Un comerciante tiene 3 variedades de bolígrafos ‘A’, ‘B’ y ‘C’. Meenu compró 1 pluma de cada variedad por un total de Rs 21. Jeevan compró 4 plumas de la variedad ‘A’, 3 plumas de la variedad ‘B’ y 2 plumas de la variedad ‘C’ por Rs 60. Mientras que Shikha compró 6 plumas de la variedad ‘A ‘, 2 bolígrafos de la variedad ‘B’ y 3 bolígrafos de la variedad ‘C’ por Rs 70. Utilizando el método de array, encuentre el costo de cada variedad de bolígrafos.
Solución:
Supongamos que hay 3 variedades de pluma A, B y C
A + B + C = 21
4A + 3B + 2C = 60
6A + 2B + 3C = 70
donde, P =
, Q =
|P| = -5
Por lo tanto, obtenemos X = P -1 Q
adj P =
=
Entonces, X =
=
=
Por lo tanto, X =
Por lo tanto, el costo de la variedad de bolígrafos para A, B y C es Rs 5, Rs 8 y Rs 8 respectivamente.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA