MCD de dos números es el número más grande que los divide a ambos. Una forma sencilla de encontrar el MCD es factorizar ambos números y multiplicar factores comunes.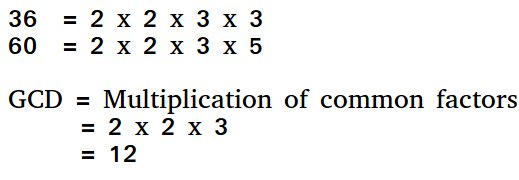
// Java program to demonstrate working of extended
// Euclidean Algorithm
import java.util.*;
import java.lang.*;
class GFG {
// extended Euclidean Algorithm
public static int gcdExtended(int a, int b, int x, int y)
{
// Base Case
if (a == 0) {
x = 0;
y = 1;
return b;
}
int x1 = 1, y1 = 1; // To store results of recursive call
int gcd = gcdExtended(b % a, a, x1, y1);
// Update x and y using results of recursive
// call
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
// Driver Program
public static void main(String[] args)
{
int x = 1, y = 1;
int a = 35, b = 15;
int g = gcdExtended(a, b, x, y);
System.out.print("gcd(" + a + ", " + b + ") = " + g);
}
}
// Code Contributed by Mohit Gupta_OMG <(0-o)>
Producción:
gcd(35, 15) = 5
Consulte el artículo completo sobre algoritmos euclidianos básicos y extendidos para obtener más detalles.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA