Función gamma – Barcelona Geeks

La función gamma es una extensión comúnmente utilizada de la función factorial para números complejos. La función gamma se define para todos los números complejos excepto los enteros no positivos.

La función gamma denotada por $\Gamma\izquierda (p \derecha)$ se define como:
$\Gamma\left(p \right) = \int_{0}^{\infty}e^{-t} t^{p-1} dt$ donde p>0.
La función gamma también se conoce como integral de Euler de segundo tipo.
Integrando la función Gamma por partes obtenemos,
$\Gamma\left (p+1 \right) = \int_{0}^{\infty}e^{-t} t^{p} dt$
$=-e^{-t} t^p \Biggr |_{0}^{\infty}+p\int_{0}^{\infty}e^{-t} t^{p-1} dt$
$=0+p\Gamma\left (p \right)$
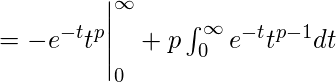
Así $\Gamma\left (p+1 \right) = p\Gamma\left (p \right)$

Algunos resultados estándar:

$\Gamma\left (1/2 \right) = \sqrt \pi$
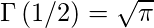
Sabemos que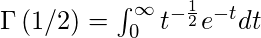 $\Gamma\left(1/2 \right) = \int_{0}^{\infty}t^{-\frac{1}{2}}e^{-t} dt$
Poner t=u^2
Por lo tanto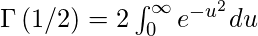 $\Gamma\left(1/2 \right) = 2\int_{0}^{\infty}e^{{-u^2}}du$
$\Gamma\left(1/2 \right) .\Gamma\left(p \right) = (2\int_{0}^{\infty}e^{{-u^2}}du)(2\int_{0}^{\infty}e^{{-u^2}}du)$
$=4\int_{0}^{\infty} \int_{0}^{\infty}e^{-{u^2 + v^2}} du dv$
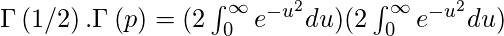
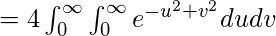
Ahora cambiando a coordenadas polares usando u = r cosθ y v = r sinθ
Por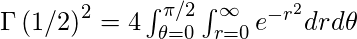 ${\Gamma\left(1/2 \right)}^2 = 4\int_{\theta=0}^{\pi/2}\int_{r=0}^{\infty}e^{-{r^2}} dr d\theta$
$=4\int_{0}^{\pi/2} -\frac{1}{2}e^{-r^2}\Biggr|_{r=0}^{\infty}$
$=2\int_{0}^{\pi/2}d\theta = 2.\theta \Biggr|_{0}^{\pi/2}=\pi$
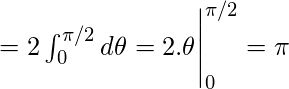
lo tanto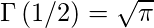 $\Gamma\left (1/2 \right) = \sqrt \pi$
$\Gamma\left(n+1 \right) = (m+1)^{n+1}(-1)^n \int_{0}^{1}x^m (ln x)^n dx$
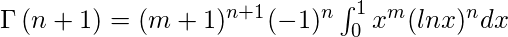
Donde n es un entero positivo y m>-1
Ponga x=e^-y tal que dx=-e ^-y dy=-x dy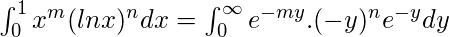
$\int_{0}^{1}x^m(ln x)^n dx= \int_{0}^{\infty}e^{-my} . (-y)^n e^{-y} dy$
$(-1)^n \int_{0}^{\infty} y^n . e^{-(m+1)y} dy$
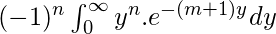
Ponga (m+1)y = u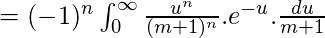
$=(-1)^n \int_{0}^{\infty}\frac{u^n}{(m+1)^n}.e^{-u} .\frac{du}{m+1}$
$=\frac{(-1)^n}{(m+1)^n+1}\int_{0}^{\infty}e^{-u} .u^n du = \frac{(-1)^n}{(m+1)^{n+1}}.\Gamma\left(n+1\right)$

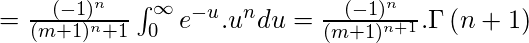
Ejemplo-1:
Calcular $\Gamma\left(4.5\right).$

Explicación:
Usando $\Gamma\left(p+1\right)=p\Gamma\left(p\right)$
$\Gamma\left(4.5\right)=\Gamma\left(3.5+1 \right)=3.5\Gamma\left(3.5\right)$
$=(3.5)(2.5)\Gamma\left(2.5\right)$
$=(3.5)(2.5)(1.5)\Gamma\left(1.5\right)$
$=(3.5)(2.5)(1.5)(0.5)\Gamma\left(0.5\right)$
Sabemos $\Gamma\left(0.5\right)=\sqrt\pi$
Así $\Gamma\left(4.5\right)=6.5625\sqrt\pi$

Ejemplo-2:
Evaluar $I=\int_{0}^{\infty}x^4 e^-{x^4} dx$

Explicación:
poner x ⁴ = t, 4x ³ dx = dt, dx = ¼ t ^-3/4 dt
$I=\int_{0}^{\infty}t.e^{-t} \frac{t^{-3/4}}{4}dt$
$= \frac{1}{4}\int_{0}^{\infty}e^{-t} t^{3/4} dt$
$= \frac{1}{4}\Gamma\left(1+\frac{1}{4}\right)$
$= \frac{1}{4}\Gamma\left(\frac{5}{4}\right)$

Publicación traducida automáticamente

Artículo escrito por mohitg593 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta