Sea G un grafo no dirigido ponderado y e una arista con peso máximo en G. Supongamos que hay un árbol de expansión de peso mínimo en G que contiene la arista e. ¿Cuál de las siguientes afirmaciones es siempre VERDADERA?
(A) Existe un conjunto de corte en G que tiene todos los bordes de peso máximo.
(B) Existe un ciclo en G que tiene todas las aristas de peso máximo
(C) La arista e no puede estar contenida en un ciclo.
(D) Todas las aristas en G tienen el mismo peso
Respuesta: (A)
Explicación: Antecedentes: dado un gráfico conectado y no dirigido, un árbol de expansión de ese gráfico es un subgráfico que es un árbol y conecta todos los vértices entre sí.
- Un árbol de expansión tiene exactamente V – 1 aristas.
- Un solo gráfico puede tener muchos árboles de expansión diferentes. Un árbol de expansión mínimo (MST) o un árbol de expansión de peso mínimo para un gráfico ponderado, conectado y no dirigido es un árbol de expansión con un peso menor o igual que el peso de cualquier otro árbol de expansión. El peso de un árbol de expansión es la suma de los pesos asignados a cada borde del árbol de expansión.
- Puede haber más de un árbol de expansión posible de un gráfico. Por ejemplo, el gráfico de esta pregunta tiene 6 posibles árboles de expansión.
- MST tiene el borde más ligero de cada corte. Recuerde el algoritmo de Prim que básicamente selecciona el borde más claro de cada corte.
Opciones de esta pregunta:
a) Existe un corte en G que tiene todos los bordes de peso máximo : esto es correcto. Si hay un borde más pesado en MST, entonces existe un corte con todos los bordes con un peso igual al borde más pesado. Véase el punto 4 discutido en los antecedentes anteriores.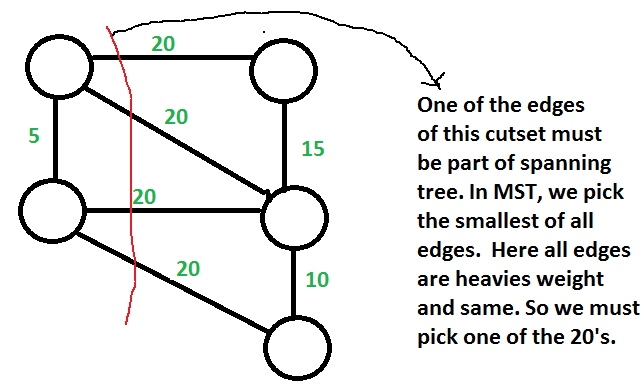
b) Existe un ciclo en G que tiene todas las aristas de peso máximo: No siempre es VERDADERO. El conjunto de corte del borde más pesado puede contener solo un borde. De hecho, puede haber un borde general de peso pesado que sea parte de MST (Considere un gráfico con dos componentes que están conectados por un solo borde y este borde es el pesado)
c) La arista e no puede estar contenida en un ciclo. No siempre es cierto. El curset puede formar un ciclo con otros bordes.
d) Todas las aristas en G tienen el mismo peso No siempre Cierto. Como se discutió en la opción b, solo puede haber un borde de mayor peso.
Cuestionario de esta pregunta
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA