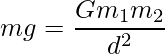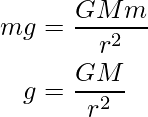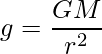Durante el paracaidismo, cuando un paracaidista salta del avión, hay un aumento repentino en la velocidad de caída, el aumento se debe a la aceleración de la gravedad y la fuerza que atrae al cuerpo, es decir, la fuerza gravitacional. Además, cuando el paracaidista abre el paracaídas, el paracaídas se opone a la gravedad y disminuye la velocidad, de modo que la persona aterriza con seguridad. También se observa que cuando una pelota se mueve hacia arriba exhibe menos velocidad que cuando baja. Todo esto se debe a la aceleración, que se produce debido a la fuerza de la gravedad.
Fuerza gravitacional
La atracción de los objetos hacia la tierra se conoce como fuerza de gravedad o gravedad. Cada objeto en el universo, ya sea grande o pequeño, ejerce una fuerza sobre todos los demás objetos. Por lo tanto, esta fuerza se conoce como fuerza gravitacional .
por ejemplo: la fuerza que actúa entre dos libros o dos objetos en la superficie de la Tierra.
Por otra parte, la fuerza gravitacional también se define como cualquier fuerza que atrae a dos objetos con una masa. Además, esta fuerza gravitatoria atrae porque siempre trata de juntar las masas y nunca las separa, ya que es una fuerza de atracción. Además, cada objeto, incluyéndote a ti, es atraído por todos los demás objetos en todo el universo y esto se llama la Ley de Gravitación Universal de Newton o la fórmula gravitacional.
Se declara como:
donde, F G es la constante gravitatoria,
G es la constante gravitacional \left(6.67\times10^{-11}\text{N}\cdot\text{m}^2/\text{kg}^2\right),
d es la distancia entre las dos masas,
M y m son las masas de los dos objetos en contacto.
La unidad SI de la fuerza gravitacional es Newton (N).
Aceleración debida a la gravedad
Cuando un cuerpo cae hacia la tierra experimenta un cambio en su aceleración debido a la fuerza gravitacional de la tierra. Esta aceleración se llama aceleración debida a la gravedad. Esta es la aceleración que alcanza un objeto debido a la fuerza gravitatoria.
La unidad SI de aceleración debida a la gravedad (g) es m/s² .
Ya que, la aceleración debida a la gravedad tiene una magnitud así como una dirección. Por lo tanto, es una cantidad vectorial .
Su valor estándar sobre la superficie de la tierra al nivel del mar es de 9,8 m/s² .
Matemáticamente, la aceleración debida a la gravedad es directamente proporcional a la masa del objeto e inversamente proporcional a la distancia desde el centro de masa, dado como:
![]()
o
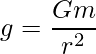
donde, G es la constante gravitacional,
m es la masa del cuerpo y
r es la distancia desde el centro.
Derivación de la fórmula de la aceleración de la gravedad
Según la segunda ley del movimiento:
F = mamá
Pero, en el caso de un cuerpo en caída libre, la fuerza es igual al producto de la masa del cuerpo y la aceleración debida a la gravedad.
F = mg ……(1)
Pero, según la ley universal de la gravitación:
……(2)
Ahora, de la ecuación (1) y (2),
Considere un caso ideal en el que el objeto se coloca cerca de la tierra, por lo tanto, la distancia entre la tierra y el objeto será el radio de la tierra, así que reemplace d con r y reorganice la expresión anterior para g como:
Cálculo del valor de la aceleración de la gravedad
La aceleración de la gravedad se expresa como:
Aquí, sustituya G por 6,67 × 10 -11 Nm 2 kg -2 , M por 6 × 10 24 kg y r por 6,4 × 10 6 m en la expresión anterior para calcular g en la superficie de la Tierra.
Factor que afecta la aceleración debida a la gravedad
- La forma de la tierra: como se sabe, la forma de la tierra no es esférica, es bastante ovalada, por lo que la fuerza gravitacional es diferente en diferentes lugares. La fuerza de atracción es máxima en el polo de la tierra aproximadamente 9,82 m/s 2 ya que el radio de la tierra es mínimo en el polo. Mientras que la fuerza de gravedad es mínima en el ecuador de la tierra aproximadamente 9,78 m/s 2 ya que el radio de la tierra es máximo en el ecuador

- Altitud: Cuando un cuerpo se aleja de la superficie de la tierra, la fuerza de atracción disminuye a medida que aumenta la distancia entre la tierra y el cuerpo.
- Profundidad: Cuando un cuerpo se introduce en la superficie terrestre, la aceleración debida a la gravedad se hace menor.
Efectos sobre g debido a la profundidad D

Considere un objeto de masa m dentro de la tierra de masa M a la profundidad D.
La aceleración de la gravedad en la superficie de la Tierra en términos de densidad es:
gramo = 4/3 x πρ x RG
en la profundidad D
g D = 4/3 x πρ x (RD)G
al dividir ambas ecuaciones obtenemos
gramo re = gx πρ x (RD)
Ahora pueden ser posibles dos casos:
Caso 1: Si la profundidad D es igual al radio de la tierra, es decir, D = R, entonces:
gramo re = 0
Caso 2: Si la profundidad D = 0, es decir, el objeto está en la superficie de la tierra, entonces
gramo re = gramo
Efectos sobre g debido a la altura h

Si un objeto se coloca a cierta altura h, entonces el valor de d será (r+h) entonces,
g h = GM/(r+h) 2
= GM/r 2 (1+h/r) 2
= (GM/r 2 )/(1+h/r) 2
= g / (1+h/r) 2 (Ya que, g = GM/r 2 )
Cuando h es mucho menor que el radio de la tierra, el valor de g a la altura h viene dado por:
g h = g/(1 – 2h/r)
Problemas de muestra
Aquí hay algunos problemas resueltos que se basan en los temas discutidos anteriormente.
Problema 1: Se coloca un cuerpo a una altura de 2 x 10 6 m de la superficie terrestre que tiene una masa de 20 kg. ¿Encuentra la aceleración debida a la gravedad del cuerpo?
Solución:
Dado que,
La altura del cuerpo, h es de 2 x 10 6 m.
La masa del cuerpo, m es de 20 kg.
Por la fórmula para g a una altura h es:
gramo h = gramo / (1+h/r) 2
Aquí, g es la aceleración de la gravedad, h es la altura y r es el radio de la Tierra.
Sustituye h por 2 x 10 6 m, g por 9,8 ms -2 y r por 6,4 x 10 6 m en la expresión anterior para calcular g h .
g h = 9.8 /(1+(2×10 6 / 6×10 6 ))
= 7,35 ms -2
Por tanto, la aceleración debida a la gravedad del cuerpo a la altura h es de 7,35 ms -2 .
Problema 2: Se coloca un cuerpo de masa m en la tierra y luego en la luna. ¿Encuentra la relación entre la aceleración de la gravedad en la Tierra y la Luna? (masa de la tierra = 5,98 x 10 24 Kg, masa de la luna = 7,36 x 10 22 Kg, radio de la tierra = 6,37 x 10 6 m, radio de la luna = 1,74 x 10 6 m).
Solución:
La aceleración de la gravedad es:
g=GM/r 2
Aquí, G es la constante de gradación. M es la masa y r es el radio de la Tierra.
La aceleración de la gravedad en la Tierra es:
sol mi = sol x metro mi /r mi 2 ……(1)
La aceleración de la gravedad en la Luna es:
gramo metro = gramo x metro metro /r metro 2 ……(2)
Divida la ecuación (1) por la ecuación (2) como:
gramo mi / gramo metro = ( Metro mi xr metro 2 )/( Metro metro xr mi 2 )
Sustituya los valores dados en la expresión anterior para calcular la relación de aceleración debida a la gravedad en la Tierra respecto a la Luna.
gramo mi / gramo metro = 6.062 ≈ 6
Por lo tanto, la relación entre la aceleración debida a la gravedad en la Tierra y la Luna es igual a 6:1.
Problema 3: Se coloca un cuerpo en el interior de la tierra a una profundidad d=1,5 x 10 6 m. ¿ Encuentra la aceleración debida a la gravedad del cuerpo? Tome la densidad de la tierra 5515 kg/m 3 .
Solución:
La aceleración de la gravedad en términos de densidad es:
g=4/3 x πρ x RG
Aquí, ρ es la densidad, R es el radio y G es la constante gravitacional.
Y, en la profundidad d es:
gramo re = 4/3 x πρ x (Rd)G
= 4/3 x 5515 x (6 x 10 6 – 1,5 x 10 6 ) x 6,67 x 10 -11
= 0,206 m/ s2
Por tanto, la aceleración debida a la gravedad del cuerpo es igual a 0,206 m/s 2 .
Problema 4: ¿Cuál será la disminución en el valor de g cuando un cuerpo se mueve una distancia de R/2 sobre la superficie terrestre?
Solución:
La aceleración de la gravedad a una altura h es:
gramo h = gramo / (1+h/R) 2
Ahora, se da que: h = R/2.
Por lo tanto, la expresión anterior se convierte en:
g h = g/(1+R/2R) 2
= g/ (3/2) 2
= 4/9 x g
Por lo tanto, los valores de g disminuyen 4/9 veces.
Problema 5: Un planeta tiene un radio y masa son la mitad de los de la tierra. ¿Encuentre la aceleración debida a la gravedad en el planeta?
Solución:
Dado que,
El radio del planeta, r p = 2r.
La masa del planeta, M p = 2M
La fórmula para calcular la aceleración debida a la gravedad del planeta,
g p = GM p / r p 2
= (2GM) / (2r) 2
= (1/2) GM/r
= 1/2 xg (Ya que, g=GM/r 2 )
Por lo tanto, la aceleración debida a la gravedad en el planeta es la mitad de la aceleración debida a la gravedad en la Tierra.