Hemos visto varios métodos con diferentes complejidades de tiempo para calcular LCA en un árbol n-ario:
Método 1: método ingenuo (mediante el cálculo de la ruta de la raíz al Node) | O(n) por consulta
Método 2: uso de la descomposición Sqrt | O(sqrt H)
Método 3: Uso del enfoque de DP de array dispersa | O (inicio de sesión)
Estudiemos otro método que tiene un tiempo de consulta más rápido que todos los métodos anteriores. Entonces, nuestro objetivo será calcular LCA en tiempo constante ~ O(1) . Veamos cómo podemos lograrlo.
Método 4: Uso de consulta de rango mínimo
Hemos discutido LCA y RMQ para el árbol binario . Aquí discutimos la conversión del problema LCA al problema RMQ para el árbol n-ario.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Concepto clave: en este método, reduciremos nuestro problema LCA a un problema RMQ (consulta mínima de rango) sobre una array estática. Una vez que hagamos eso, relacionaremos las consultas mínimas de rango con las consultas LCA requeridas.
El primer paso será descomponer el árbol en una array lineal plana. Para ello podemos aplicar el camino de Euler. El paseo de Euler dará el recorrido preordenado del gráfico. Así que realizaremos un Euler Walk en el árbol y almacenaremos los Nodes en una array a medida que los visitamos. Este proceso reduce la estructura de datos del árbol a una array lineal simple.
Considere el siguiente árbol y el euler camina sobre él:
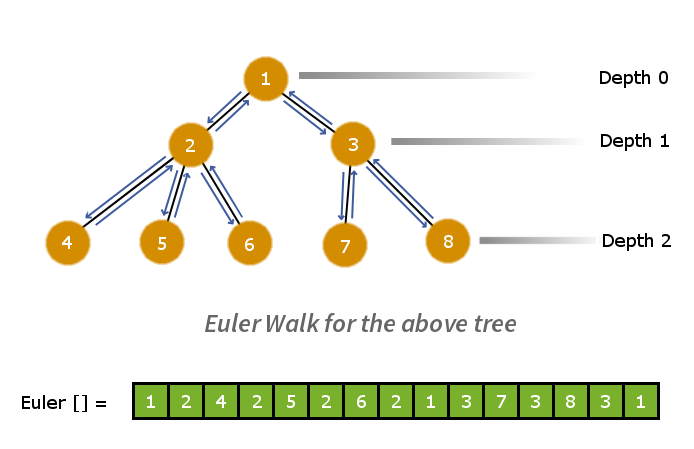
Ahora pensemos en términos generales: considere dos Nodes en el árbol. Habrá exactamente una ruta que conecte ambos Nodes y el Node que tenga el valor de profundidad más pequeño en la ruta será el LCA de los dos Nodes dados.
Ahora tome dos Nodes distintos, digamos u y v en la array de caminata de Euler. Ahora todos los elementos en el camino de u a v estarán entre el índice de los Nodes u y v en la array de paseo de Euler. Por lo tanto, solo necesitamos calcular el Node con la profundidad mínima entre el índice del Node u y el Node v en la array de Euler.
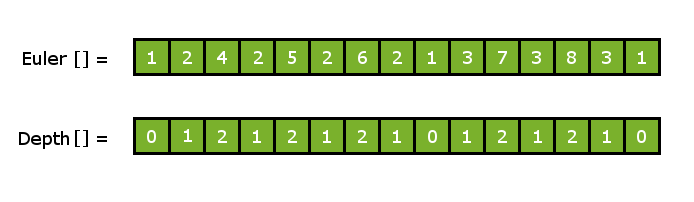
Para ello mantendremos otro arreglo que contendrá la profundidad de todos los Nodes correspondientes a su posición en el arreglo de paseo de Euler para que podamos aplicarle nuestro algoritmo RMQ.
A continuación se muestra la array de caminata de Euler paralela a su array de seguimiento de profundidad.
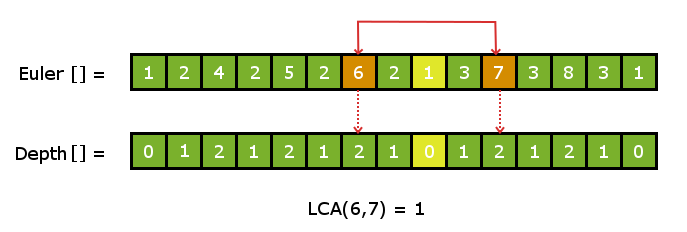
Ejemplo: – Considere dos Nodes, el Node 6 y el Node 7 en la array de euler. Para calcular el LCA del Node 6 y el Node 7, buscamos el valor de profundidad más pequeño para todos los Nodes entre el Node 6 y el Node 7.
Por lo tanto, el Node 1 tiene el valor de profundidad más pequeño = 0 y, por lo tanto, es el LCA para el Node 6 y el Node 7.
Implementación:-
We will be maintaining three arrays 1)Euler Path
2)Depth array
3)First Appearance Index
La array Euler Path y Depth es la misma que se describió anteriormente
First Appearance Index FAI[] : First Appearance index Array almacenará el índice para la primera posición de cada Node en la array Euler Path. FAI[i] = Primera aparición del i-ésimo Node en el arreglo de Euler Walk.
La implementación para el método anterior se da a continuación: –
Implementación:
C++
// C++ program to demonstrate LCA of n-ary tree
// in constant time.
#include "bits/stdc++.h"
using namespace std;
#define sz 101
vector < int > adj[sz]; // stores the tree
vector < int > euler; // tracks the eulerwalk
vector < int > depthArr; // depth for each node corresponding
// to eulerwalk
int FAI[sz]; // stores first appearance index of every node
int level[sz]; // stores depth for all nodes in the tree
int ptr; // pointer to euler walk
int dp[sz][18]; // sparse table
int logn[sz]; // stores log values
int p2[20]; // stores power of 2
void buildSparseTable(int n)
{
// initializing sparse table
memset(dp,-1,sizeof(dp));
// filling base case values
for (int i=1; i<n; i++)
dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i;
// dp to fill sparse table
for (int l=1; l<15; l++)
for (int i=0; i<n; i++)
if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1)
dp[i][l] =
(depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])?
dp[i+p2[l-1]][l-1] : dp[i][l-1];
else
break;
}
int query(int l,int r)
{
int d = r-l;
int dx = logn[d];
if (l==r) return l;
if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]])
return dp[r-p2[dx]][dx];
else
return dp[l][dx];
}
void preprocess()
{
// memorizing powers of 2
p2[0] = 1;
for (int i=1; i<18; i++)
p2[i] = p2[i-1]*2;
// memorizing all log(n) values
int val = 1,ptr=0;
for (int i=1; i<sz; i++)
{
logn[i] = ptr-1;
if (val==i)
{
val*=2;
logn[i] = ptr;
ptr++;
}
}
}
/**
* Euler Walk ( preorder traversal)
* converting tree to linear depthArray
* Time Complexity : O(n)
* */
void dfs(int cur,int prev,int dep)
{
// marking FAI for cur node
if (FAI[cur]==-1)
FAI[cur] = ptr;
level[cur] = dep;
// pushing root to euler walk
euler.push_back(cur);
// incrementing euler walk pointer
ptr++;
for (auto x:adj[cur])
{
if (x != prev)
{
dfs(x,cur,dep+1);
// pushing cur again in backtrack
// of euler walk
euler.push_back(cur);
// increment euler walk pointer
ptr++;
}
}
}
// Create Level depthArray corresponding
// to the Euler walk Array
void makeArr()
{
for (auto x : euler)
depthArr.push_back(level[x]);
}
int LCA(int u,int v)
{
// trivial case
if (u==v)
return u;
if (FAI[u] > FAI[v])
swap(u,v);
// doing RMQ in the required range
return euler[query(FAI[u], FAI[v])];
}
void addEdge(int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
int main(int argc, char const *argv[])
{
// constructing the described tree
int numberOfNodes = 8;
addEdge(1,2);
addEdge(1,3);
addEdge(2,4);
addEdge(2,5);
addEdge(2,6);
addEdge(3,7);
addEdge(3,8);
// performing required precalculations
preprocess();
// doing the Euler walk
ptr = 0;
memset(FAI,-1,sizeof(FAI));
dfs(1,0,0);
// creating depthArray corresponding to euler[]
makeArr();
// building sparse table
buildSparseTable(depthArr.size());
cout << "LCA(6,7) : " << LCA(6,7) << "\n";
cout << "LCA(6,4) : " << LCA(6,4) << "\n";
return 0;
}
Java
// Java program to demonstrate LCA of n-ary
// tree in constant time.
import java.util.ArrayList;
import java.util.Arrays;
class GFG{
static int sz = 101;
@SuppressWarnings("unchecked")
// Stores the tree
static ArrayList<Integer>[] adj = new ArrayList[sz];
// Tracks the eulerwalk
static ArrayList<Integer> euler = new ArrayList<>();
// Depth for each node corresponding
static ArrayList<Integer> depthArr = new ArrayList<>();
// to eulerwalk
// Stores first appearance index of every node
static int[] FAI = new int[sz];
// Stores depth for all nodes in the tree
static int[] level = new int[sz];
// Pointer to euler walk
static int ptr;
// Sparse table
static int[][] dp = new int[sz][18];
// Stores log values
static int[] logn = new int[sz];
// Stores power of 2
static int[] p2 = new int[20];
static void buildSparseTable(int n)
{
// Initializing sparse table
for(int i = 0; i < sz; i++)
{
for(int j = 0; j < 18; j++)
{
dp[i][j] = -1;
}
}
// Filling base case values
for(int i = 1; i < n; i++)
dp[i - 1][0] = (depthArr.get(i) >
depthArr.get(i - 1)) ?
i - 1 : i;
// dp to fill sparse table
for(int l = 1; l < 15; l++)
for(int i = 0; i < n; i++)
if (dp[i][l - 1] != -1 &&
dp[i + p2[l - 1]][l - 1] != -1)
dp[i][l] = (depthArr.get(dp[i][l - 1]) >
depthArr.get(
dp[i + p2[l - 1]][l - 1])) ?
dp[i + p2[l - 1]][l - 1] :
dp[i][l - 1];
else
break;
}
static int query(int l, int r)
{
int d = r - l;
int dx = logn[d];
if (l == r)
return l;
if (depthArr.get(dp[l][dx]) >
depthArr.get(dp[r - p2[dx]][dx]))
return dp[r - p2[dx]][dx];
else
return dp[l][dx];
}
static void preprocess()
{
// Memorizing powers of 2
p2[0] = 1;
for(int i = 1; i < 18; i++)
p2[i] = p2[i - 1] * 2;
// Memorizing all log(n) values
int val = 1, ptr = 0;
for(int i = 1; i < sz; i++)
{
logn[i] = ptr - 1;
if (val == i)
{
val *= 2;
logn[i] = ptr;
ptr++;
}
}
}
// Euler Walk ( preorder traversal) converting
// tree to linear depthArray
// Time Complexity : O(n)
static void dfs(int cur, int prev, int dep)
{
// Marking FAI for cur node
if (FAI[cur] == -1)
FAI[cur] = ptr;
level[cur] = dep;
// Pushing root to euler walk
euler.add(cur);
// Incrementing euler walk pointer
ptr++;
for(Integer x : adj[cur])
{
if (x != prev)
{
dfs(x, cur, dep + 1);
// Pushing cur again in backtrack
// of euler walk
euler.add(cur);
// Increment euler walk pointer
ptr++;
}
}
}
// Create Level depthArray corresponding
// to the Euler walk Array
static void makeArr()
{
for(Integer x : euler)
depthArr.add(level[x]);
}
static int LCA(int u, int v)
{
// Trivial case
if (u == v)
return u;
if (FAI[u] > FAI[v])
{
int temp = u;
u = v;
v = temp;
}
// Doing RMQ in the required range
return euler.get(query(FAI[u], FAI[v]));
}
static void addEdge(int u, int v)
{
adj[u].add(v);
adj[v].add(u);
}
// Driver code
public static void main(String[] args)
{
for(int i = 0; i < sz; i++)
{
adj[i] = new ArrayList<>();
}
// Constructing the described tree
int numberOfNodes = 8;
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(2, 6);
addEdge(3, 7);
addEdge(3, 8);
// Performing required precalculations
preprocess();
// Doing the Euler walk
ptr = 0;
Arrays.fill(FAI, -1);
dfs(1, 0, 0);
// Creating depthArray corresponding to euler[]
makeArr();
// Building sparse table
buildSparseTable(depthArr.size());
System.out.println("LCA(6,7) : " + LCA(6, 7));
System.out.println("LCA(6,4) : " + LCA(6, 4));
}
}
// This code is contributed by sanjeev2552
LCA(6,7) : 1 LCA(6,4) : 2
Nota: Estamos precalculando toda la potencia de 2 necesaria y también precalculando todos los valores de registro necesarios para garantizar una complejidad de tiempo constante por consulta. De lo contrario, si hiciéramos un cálculo de registro para cada operación de consulta, nuestra complejidad de tiempo no habría sido constante.
Complejidad de tiempo: el proceso de conversión de LCA a RMQ lo realiza Euler Walk, que toma O (n) tiempo.
El preprocesamiento de la tabla dispersa en RMQ requiere tiempo O(nlogn) y responder a cada consulta es un proceso de tiempo constante. Por lo tanto, la complejidad temporal general es O(nlogn) – preprocesamiento y O(1) para cada consulta.
Este artículo es una contribución de Nitish Kumar . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA