Algoritmo de cifrado RC5 – Part 1

RC5 es un algoritmo de cifrado de bloque de clave simétrica diseñado por Ron Rivest en 1994. Se destaca por ser simple, rápido (debido a que usa solo operaciones informáticas primitivas como XOR, shift, etc.) y consume menos memoria.

Ejemplo:

Key : 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
Plain Text : 00000000 00000000
Cipher Text : EEDBA521 6D8F4B15

RC5 es un cifrado de bloque y aborda dos bloques de palabras a la vez.
Según el tamaño del bloque de texto sin formato de entrada, el número de rondas y el tamaño de la clave, se pueden definir varias instancias de RC5 y cada instancia se denota como RC5-w/r/b donde w = tamaño de palabra en bits, r = número de rondas y b =tamaño de clave en bytes.
Los valores permitidos son:

Parámetro	Valor posible
tamaño de bloque/palabra (bits)	16, 32, 64
Número de rondas	0 – 255
Tamaño de clave (bytes)	0 – 255

Nota: dado que, a la vez, RC5 usa bloques de 2 palabras, el tamaño del bloque de texto sin formato puede ser de 32, 64 o 128 bits.

Notación utilizada en el algoritmo:

Símbolo	Operación
x <<< y	Desplazamiento cíclico a la izquierda de x por y bits
+	Adición en complemento a dos de palabras donde la suma es módulo
^	OR exclusivo bit a bit

Paso-1: Inicialización de las constantes P y Q.
RC5 hace uso de 2 constantes mágicas P y Q cuyo valor está definido por el tamaño de palabra w.

Tamaño de palabra (bits)	P (hexadecimal)	Q (hexadecimal)
dieciséis	b7e1	9e37
32	b7e15163	9e3779b9
64	b7e151628aed2a6b	9e3779b97f4a7c15

Para cualquier otro tamaño de palabra, P y Q se pueden determinar como:

P = Odd((e-2)) 
Q = Odd((-2))

Aquí, Odd(x) es el entero impar más cercano a x, e es la base de los logaritmos naturales y es la proporción áurea.

Paso 2: Convertir la clave secreta K de bytes a palabras.
La clave secreta K de tamaño b bytes se usa para inicializar la array L que consiste en c palabras donde c = b/u, u = w/8 y w = tamaño de palabra usado para esa instancia particular de RC5. Por ejemplo, si elegimos w=32 bits y la clave k tiene un tamaño de 96 bytes, u=32/8=4, c=b/u=96/4=24.
L se inicializa previamente en el valor 0 antes de agregarle la clave secreta K.

for i=b-1 to 0
    L[i/u] = (L[u/i] <<< 8) + K[i]

Paso 3: inicialización de la subclave S.
La subclave S de tamaño t=2(r+1) se inicializa utilizando las constantes mágicas P y Q.

S[0] = P
for i = 1 to 2(r+1)-1
    S[i] = S[i-1] + Q)

Paso 4: mezcla de subclaves.
El algoritmo de cifrado RC5 utiliza la clave secundaria S. L es simplemente una array temporal formada sobre la base de la clave secreta ingresada por el usuario.
Mezcle la clave secreta del usuario con S y L.

i = j = 0
A = B = 0
do 3 * max(t, c) times:
    A = S[i] = (S[i] + A + B) <<< 3
    B = L[j] = (L[j] + A + B) <<< (A + B)
    i = (i + 1) % t
    j = (j + 1) % c

Paso 5: Cifrado.
Dividimos el bloque de texto sin formato de entrada en dos registros A y B, cada uno de tamaño w bits. Después de someterse al proceso de cifrado, el resultado de A y B juntos forma el bloque de texto cifrado.
Algoritmo de cifrado RC5:

1. Inicialización única de los bloques de texto sin formato A y B agregando S[0] y S[1] a A y B respectivamente. Estas operaciones son mod .
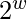2. XOR A y B. A=A^B
3. Desplazamiento cíclico a la izquierda nuevo valor de A por B bits.
4. Agregue S[2*i] a la salida del paso anterior. Este es el nuevo valor de A.
5. XOR B con nuevo valor de A y almacenar en B.
6. Desplazamiento cíclico a la izquierda nuevo valor de B por A bits.
7. Agregue S[2*i+1] a la salida del paso anterior. Este es el nuevo valor de B.
8. Repita todo el procedimiento (excepto la inicialización única) r veces.

A = A + S[0] 
B = B + S[1]
for i = 1 to r do:
    A = ((A ^ B) <<< B) + S[2 * i]
    B = ((B ^ A) <<< A) + S[2 * i + 1]
return A, B

Alternativamente, RC5 Decryption se puede definir como:

for i = r down to 1 do:
    B = ((B - S[2 * i + 1]) >>> A) ^ A
    A = ((A - S[2 * i]) >>> B) ^ B
B = B - S[1]
A = A - S[0]
return A, B