El algoritmo de eliminación inversa está estrechamente relacionado con el algoritmo de Kruskal . En el algoritmo de Kruskal lo que hacemos es: Ordenar los bordes por orden creciente de sus pesos. Después de clasificar, seleccionamos los bordes uno por uno en orden creciente. Incluimos el borde seleccionado actual si al incluir esto en el árbol de expansión no se forma ningún ciclo hasta que haya bordes V-1 en el árbol de expansión, donde V = número de vértices.
En el algoritmo Reverse Delete, clasificamos todos los bordes en orden decreciente de sus pesos. Después de clasificar, seleccionamos uno por uno los bordes en orden decreciente. Incluimos el borde seleccionado actual si la exclusión del borde actual provoca la desconexión en el gráfico actual . La idea principal es eliminar el borde si su eliminación no conduce a la desconexión del gráfico.
El algoritmo:
- Ordene todos los bordes del gráfico en orden no creciente de pesos de borde.
- Inicialice MST como el gráfico original y elimine los bordes adicionales mediante el paso 3.
- Seleccione el borde de mayor peso de los bordes restantes y verifique si al eliminar el borde se desconecta el gráfico o no .
Si se desconecta, entonces no eliminamos el borde.
De lo contrario, eliminamos el borde y continuamos.
Ilustración:
Entendamos con el siguiente ejemplo:
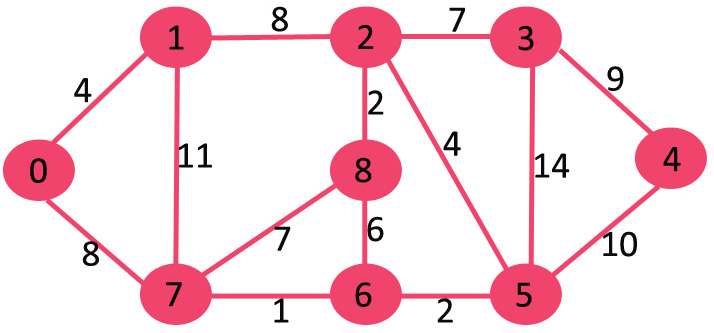
Si eliminamos el borde de peso más alto del peso 14, el gráfico no se desconecta, por lo que lo eliminamos.

A continuación eliminamos 11 ya que eliminarlo no desconecta el gráfico.

A continuación eliminamos 10 ya que eliminarlo no desconecta el gráfico.

El siguiente es 9. No podemos eliminar 9 ya que eliminarlo provoca la desconexión.

Continuamos de esta manera y los siguientes bordes permanecen en MST final.
Edges in MST (3, 4) (0, 7) (2, 3) (2, 5) (0, 1) (5, 6) (2, 8) (6, 7)
Nota: en el caso de bordes del mismo peso, podemos elegir cualquier borde del mismo peso.
Implementación:
C++
// C++ program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm
#include<bits/stdc++.h>
using namespace std;
// Creating shortcut for an integer pair
typedef pair<int, int> iPair;
// Graph class represents a directed graph
// using adjacency list representation
class Graph
{
int V; // No. of vertices
list<int> *adj;
vector< pair<int, iPair> > edges;
void DFS(int v, bool visited[]);
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int u, int v, int w);
// Returns true if graph is connected
bool isConnected();
void reverseDeleteMST();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int u, int v, int w)
{
adj[u].push_back(v); // Add w to v’s list.
adj[v].push_back(u); // Add w to v’s list.
edges.push_back({w, {u, v}});
}
void Graph::DFS(int v, bool visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
// Recur for all the vertices adjacent to
// this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFS(*i, visited);
}
// Returns true if given graph is connected, else false
bool Graph::isConnected()
{
bool visited[V];
memset(visited, false, sizeof(visited));
// Find all reachable vertices from first vertex
DFS(0, visited);
// If set of reachable vertices includes all,
// return true.
for (int i=1; i<V; i++)
if (visited[i] == false)
return false;
return true;
}
// This function assumes that edge (u, v)
// exists in graph or not,
void Graph::reverseDeleteMST()
{
// Sort edges in increasing order on basis of cost
sort(edges.begin(), edges.end());
int mst_wt = 0; // Initialize weight of MST
cout << "Edges in MST\n";
// Iterate through all sorted edges in
// decreasing order of weights
for (int i=edges.size()-1; i>=0; i--)
{
int u = edges[i].second.first;
int v = edges[i].second.second;
// Remove edge from undirected graph
adj[u].remove(v);
adj[v].remove(u);
// Adding the edge back if removing it
// causes disconnection. In this case this
// edge becomes part of MST.
if (isConnected() == false)
{
adj[u].push_back(v);
adj[v].push_back(u);
// This edge is part of MST
cout << "(" << u << ", " << v << ") \n";
mst_wt += edges[i].first;
}
}
cout << "Total weight of MST is " << mst_wt;
}
// Driver code
int main()
{
// create the graph given in above figure
int V = 9;
Graph g(V);
// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.reverseDeleteMST();
return 0;
}
Python3
# Python3 program to find Minimum Spanning Tree
# of a graph using Reverse Delete Algorithm
# Graph class represents a directed graph
# using adjacency list representation
class Graph:
def __init__(self, v):
# No. of vertices
self.v = v
self.adj = [0] * v
self.edges = []
for i in range(v):
self.adj[i] = []
# function to add an edge to graph
def addEdge(self, u: int, v: int, w: int):
self.adj[u].append(v) # Add w to v’s list.
self.adj[v].append(u) # Add w to v’s list.
self.edges.append((w, (u, v)))
def dfs(self, v: int, visited: list):
# Mark the current node as visited and print it
visited[v] = True
# Recur for all the vertices adjacent to
# this vertex
for i in self.adj[v]:
if not visited[i]:
self.dfs(i, visited)
# Returns true if graph is connected
# Returns true if given graph is connected, else false
def connected(self):
visited = [False] * self.v
# Find all reachable vertices from first vertex
self.dfs(0, visited)
# If set of reachable vertices includes all,
# return true.
for i in range(1, self.v):
if not visited[i]:
return False
return True
# This function assumes that edge (u, v)
# exists in graph or not,
def reverseDeleteMST(self):
# Sort edges in increasing order on basis of cost
self.edges.sort(key = lambda a: a[0])
mst_wt = 0 # Initialize weight of MST
print("Edges in MST")
# Iterate through all sorted edges in
# decreasing order of weights
for i in range(len(self.edges) - 1, -1, -1):
u = self.edges[i][1][0]
v = self.edges[i][1][1]
# Remove edge from undirected graph
self.adj[u].remove(v)
self.adj[v].remove(u)
# Adding the edge back if removing it
# causes disconnection. In this case this
# edge becomes part of MST.
if self.connected() == False:
self.adj[u].append(v)
self.adj[v].append(u)
# This edge is part of MST
print("( %d, %d )" % (u, v))
mst_wt += self.edges[i][0]
print("Total weight of MST is", mst_wt)
# Driver Code
if __name__ == "__main__":
# create the graph given in above figure
V = 9
g = Graph(V)
# making above shown graph
g.addEdge(0, 1, 4)
g.addEdge(0, 7, 8)
g.addEdge(1, 2, 8)
g.addEdge(1, 7, 11)
g.addEdge(2, 3, 7)
g.addEdge(2, 8, 2)
g.addEdge(2, 5, 4)
g.addEdge(3, 4, 9)
g.addEdge(3, 5, 14)
g.addEdge(4, 5, 10)
g.addEdge(5, 6, 2)
g.addEdge(6, 7, 1)
g.addEdge(6, 8, 6)
g.addEdge(7, 8, 7)
g.reverseDeleteMST()
# This code is contributed by
# sanjeev2552
C#
// C# program to find Minimum Spanning Tree
// of a graph using Reverse Delete Algorithm
using System;
using System.Collections.Generic;
// class to represent an edge
public class Edge : IComparable<Edge> {
public int u, v, w;
public Edge(int u, int v, int w)
{
this.u = u;
this.v = v;
this.w = w;
}
public int CompareTo(Edge other)
{
return this.w.CompareTo(other.w);
}
}
// Graph class represents a directed graph
// using adjacency list representation
public class Graph {
private int V; // No. of vertices
private List<int>[] adj;
private List<Edge> edges;
public Graph(int v) // Constructor
{
V = v;
adj = new List<int>[ v ];
for (int i = 0; i < v; i++)
adj[i] = new List<int>();
edges = new List<Edge>();
}
// function to Add an edge
public void AddEdge(int u, int v, int w)
{
adj[u].Add(v); // Add w to v’s list.
adj[v].Add(u); // Add w to v’s list.
edges.Add(new Edge(u, v, w));
}
// function to perform dfs
private void DFS(int v, bool[] visited)
{
// Mark the current node as visited and print it
visited[v] = true;
// Recur for all the vertices adjacent to
// this vertex
foreach(int i in adj[v])
{
if (!visited[i])
DFS(i, visited);
}
}
// Returns true if given graph is connected, else false
private bool IsConnected()
{
bool[] visited = new bool[V];
// Find all reachable vertices from first vertex
DFS(0, visited);
// If set of reachable vertices includes all,
// return true.
for (int i = 1; i < V; i++) {
if (visited[i] == false)
return false;
}
return true;
}
// This function assumes that edge (u, v)
// exists in graph or not,
public void ReverseDeleteMST()
{
// Sort edges in increasing order on basis of cost
edges.Sort();
int mst_wt = 0; // Initialize weight of MST
Console.WriteLine("Edges in MST");
// Iterate through all sorted edges in
// decreasing order of weights
for (int i = edges.Count - 1; i >= 0; i--) {
int u = edges[i].u;
int v = edges[i].v;
// Remove edge from undirected graph
adj[u].Remove(v);
adj[v].Remove(u);
// Adding the edge back if removing it
// causes disconnection. In this case this
// edge becomes part of MST.
if (IsConnected() == false) {
adj[u].Add(v);
adj[v].Add(u);
// This edge is part of MST
Console.WriteLine("({0}, {1})", u, v);
mst_wt += edges[i].w;
}
}
Console.WriteLine("Total weight of MST is {0}",
mst_wt);
}
}
class GFG {
// Driver code
static void Main(string[] args)
{
// create the graph given in above figure
int V = 9;
Graph g = new Graph(V);
// making above shown graph
g.AddEdge(0, 1, 4);
g.AddEdge(0, 7, 8);
g.AddEdge(1, 2, 8);
g.AddEdge(1, 7, 11);
g.AddEdge(2, 3, 7);
g.AddEdge(2, 8, 2);
g.AddEdge(2, 5, 4);
g.AddEdge(3, 4, 9);
g.AddEdge(3, 5, 14);
g.AddEdge(4, 5, 10);
g.AddEdge(5, 6, 2);
g.AddEdge(6, 7, 1);
g.AddEdge(6, 8, 6);
g.AddEdge(7, 8, 7);
g.ReverseDeleteMST();
}
}
// This code is contributed by cavi4762
Edges in MST (3, 4) (0, 7) (2, 3) (2, 5) (0, 1) (5, 6) (2, 8) (6, 7) Total weight of MST is 37
Notas:
- La implementación anterior es una implementación simple/ingenua del algoritmo de eliminación inversa y se puede optimizar para O(E log V (log log V) 3 ) [Fuente: Wiki ]. Pero esta complejidad de tiempo optimizada es aún menor que los algoritmos de Prim y Kruskal para MST.
- La implementación anterior modifica el gráfico original. Podemos crear una copia del gráfico si se debe conservar el gráfico original.
Este artículo es una contribución de Antra Purohit . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA