El camino euleriano es un camino en un gráfico que visita cada borde exactamente una vez. El Circuito Euleriano es un Camino Euleriano que comienza y termina en el mismo vértice.
Recomendamos encarecidamente leer primero la siguiente publicación sobre Euler Path and Circuit. “ https://www.geeksforgeeks.org/eulerian-path-and-circuit/”
En la publicación mencionada anteriormente, discutimos el problema de averiguar si un gráfico dado es euleriano o no. En esta publicación, se analiza un algoritmo para imprimir un sendero o circuito euleriano.
El siguiente es el algoritmo de Fleury para imprimir el ciclo o ciclo euleriano
- Asegúrate de que el gráfico tenga 0 o 2 vértices impares.
- Si hay 0 vértices impares, comience en cualquier lugar. Si hay 2 vértices impares, comienza en uno de ellos.
- Siga los bordes uno a la vez. Si puede elegir entre un puente y un no puente, elija siempre el no puente .
- Detente cuando te quedes sin bordes.
La idea es, «no quemar puentes « para que podamos volver a un vértice y atravesar los bordes restantes. Por ejemplo, consideremos el siguiente gráfico.
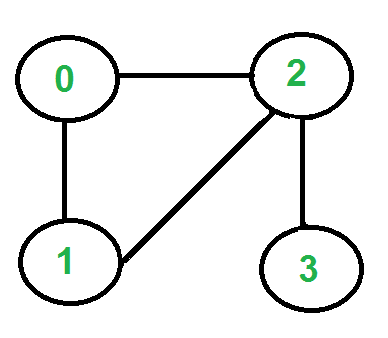
Hay dos vértices con grados impares, ‘2’ y ‘3’, y podemos iniciar caminos desde cualquiera de ellos. Comencemos el recorrido desde el vértice ‘2’.
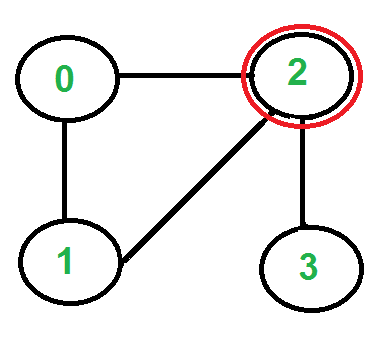
Tres aristas salen del vértice ‘2’, ¿cuál elegir? No elegimos el borde ‘2-3’ porque es un puente (no podremos volver al ‘3’). Podemos elegir cualquiera de los dos bordes restantes. Digamos que elegimos ‘2-0’. Eliminamos este borde y lo movemos al vértice ‘0’.
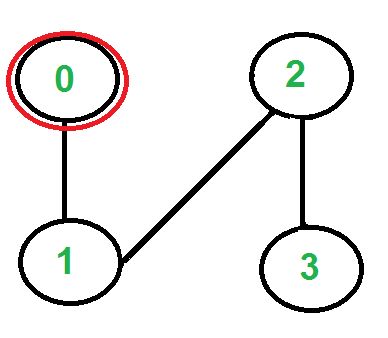
Solo hay un borde desde el vértice ‘0’, así que lo seleccionamos, lo eliminamos y lo movemos al vértice ‘1’. La gira de Euler se convierte en ‘2-0 0-1’.
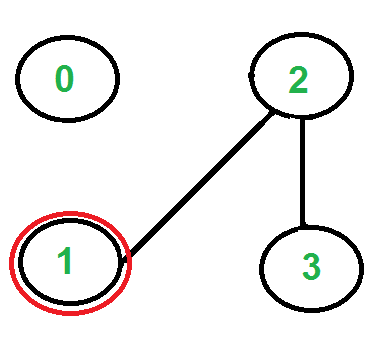
Solo hay un borde desde el vértice ‘1’, así que lo seleccionamos, lo eliminamos y lo movemos al vértice ‘2’. La gira de Euler se convierte en ‘2-0 0-1 1-2’
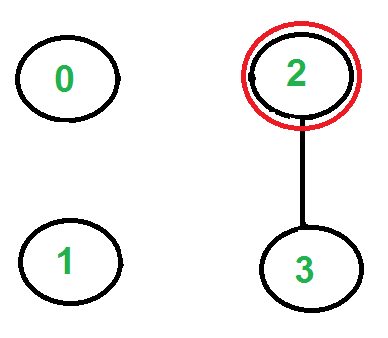
Nuevamente, solo hay un borde desde el vértice 2, por lo que lo seleccionamos, lo eliminamos y lo movemos al vértice 3. El recorrido de Euler se convierte en ‘2-0 0-1 1-2 2-3’
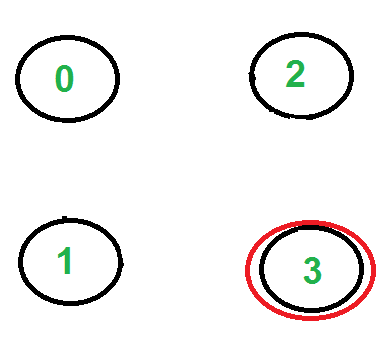
Ya no quedan más bordes, así que nos detenemos aquí. El recorrido final es ‘2-0 0-1 1-2 2-3’.
Vea esto y esto para más ejemplos.
A continuación se muestra la implementación en C++ del algoritmo anterior. En el siguiente código, se supone que el grafo dado tiene un rastro o circuito euleriano. El objetivo principal es imprimir un sendero o circuito euleriano. Podemos usar isEulerian() para verificar primero si hay un sendero o circuito euleriano en el gráfico dado.
Primero encontramos el punto de partida que debe ser un vértice impar (si hay vértices impares) y lo almacenamos en la variable ‘u’. Si hay cero vértices impares, comenzamos desde el vértice ‘0’. Llamamos a printEulerUtil() para imprimir el recorrido de Euler comenzando con u. Recorremos todos los vértices adyacentes de u, si solo hay un vértice adyacente, lo consideramos de inmediato. Si hay más de un vértice adyacente, consideramos una v adyacente solo si la arista uv no es un puente. ¿Cómo encontrar si un borde dado es un puente? Contamos varios vértices alcanzables desde u. Eliminamos el borde uv y nuevamente contamos el número de vértices alcanzables desde u. Si se reduce el número de vértices alcanzables, la arista uv es un puente. Para contar los vértices alcanzables, podemos usar BFS o DFS, hemos usado DFS en el código anterior. La función DFSCount(u) devuelve varios vértices accesibles desde u.
Una vez que se procesa un borde (incluido en el recorrido de Euler), lo eliminamos del gráfico. Para eliminar el borde, reemplazamos la entrada del vértice con -1 en la lista de adyacencia. Tenga en cuenta que simplemente eliminar el Node puede no funcionar ya que el código es recursivo y una llamada principal puede estar en el medio de la lista de adyacencia.
C++
// A C++ program print Eulerian Trail in a given Eulerian or
// Semi-Eulerian Graph
#include <algorithm>
#include <iostream>
#include <list>
#include <string.h>
using namespace std;
// A class that represents an undirected graph
class Graph {
int V; // No. of vertices
list<int>* adj; // A dynamic array of adjacency lists
public:
// Constructor and destructor
Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
~Graph() { delete[] adj; }
// functions to add and remove edge
void addEdge(int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void rmvEdge(int u, int v);
// Methods to print Eulerian tour
void printEulerTour();
void printEulerUtil(int s);
// This function returns count of vertices reachable
// from v. It does DFS
int DFSCount(int v, bool visited[]);
// Utility function to check if edge u-v is a valid next
// edge in Eulerian trail or circuit
bool isValidNextEdge(int u, int v);
};
/* The main function that print Eulerian Trail. It first
finds an odd degree vertex (if there is any) and then
calls printEulerUtil() to print the path */
void Graph::printEulerTour()
{
// Find a vertex with odd degree
int u = 0;
for (int i = 0; i < V; i++)
if (adj[i].size() & 1) {
u = i;
break;
}
// Print tour starting from oddv
printEulerUtil(u);
cout << endl;
}
// Print Euler tour starting from vertex u
void Graph::printEulerUtil(int u)
{
// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i) {
int v = *i;
// If edge u-v is not removed and it's a a valid
// next edge
if (v != -1 && isValidNextEdge(u, v)) {
cout << u << "-" << v << " ";
rmvEdge(u, v);
printEulerUtil(v);
}
}
}
// The function to check if edge u-v can be considered as
// next edge in Euler Tout
bool Graph::isValidNextEdge(int u, int v)
{
// The edge u-v is valid in one of the following two
// cases:
// 1) If v is the only adjacent vertex of u
int count = 0; // To store count of adjacent vertices
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (*i != -1)
count++;
if (count == 1)
return true;
// 2) If there are multiple adjacents, then u-v is not a
// bridge Do following steps to check if u-v is a bridge
// 2.a) count of vertices reachable from u
bool visited[V];
memset(visited, false, V);
int count1 = DFSCount(u, visited);
// 2.b) Remove edge (u, v) and after removing the edge,
// count vertices reachable from u
rmvEdge(u, v);
memset(visited, false, V);
int count2 = DFSCount(u, visited);
// 2.c) Add the edge back to the graph
addEdge(u, v);
// 2.d) If count1 is greater, then edge (u, v) is a
// bridge
return (count1 > count2) ? false : true;
}
// This function removes edge u-v from graph. It removes
// the edge by replacing adjacent vertex value with -1.
void Graph::rmvEdge(int u, int v)
{
// Find v in adjacency list of u and replace it with -1
list<int>::iterator iv
= find(adj[u].begin(), adj[u].end(), v);
*iv = -1;
// Find u in adjacency list of v and replace it with -1
list<int>::iterator iu
= find(adj[v].begin(), adj[v].end(), u);
*iu = -1;
}
// A DFS based function to count reachable vertices from v
int Graph::DFSCount(int v, bool visited[])
{
// Mark the current node as visited
visited[v] = true;
int count = 1;
// Recur for all vertices adjacent to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (*i != -1 && !visited[*i])
count += DFSCount(*i, visited);
return count;
}
// Driver program to test above function
int main()
{
// Let us first create and test graphs shown in above
// figure
Graph g1(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
return 0;
}
Java
// A Java program print Eulerian Trail
// in a given Eulerian or Semi-Eulerian Graph
import java.util.ArrayList;
// An Undirected graph using
// adjacency list representation
public class Graph {
private int vertices; // No. of vertices
private ArrayList<Integer>[] adj; // adjacency list
// Constructor
Graph(int numOfVertices)
{
// initialise vertex count
this.vertices = numOfVertices;
// initialise adjacency list
initGraph();
}
// utility method to initialise adjacency list
@SuppressWarnings("unchecked") private void initGraph()
{
adj = new ArrayList[vertices];
for (int i = 0; i < vertices; i++) {
adj[i] = new ArrayList<>();
}
}
// add edge u-v
private void addEdge(Integer u, Integer v)
{
adj[u].add(v);
adj[v].add(u);
}
// This function removes edge u-v from graph.
private void removeEdge(Integer u, Integer v)
{
adj[u].remove(v);
adj[v].remove(u);
}
/* The main function that print Eulerian Trail.
It first finds an odd degree vertex (if there
is any) and then calls printEulerUtil() to
print the path */
private void printEulerTour()
{
// Find a vertex with odd degree
Integer u = 0;
for (int i = 0; i < vertices; i++) {
if (adj[i].size() % 2 == 1) {
u = i;
break;
}
}
// Print tour starting from oddv
printEulerUtil(u);
System.out.println();
}
// Print Euler tour starting from vertex u
private void printEulerUtil(Integer u)
{
// Recur for all the vertices adjacent to this
// vertex
for (int i = 0; i < adj[u].size(); i++) {
Integer v = adj[u].get(i);
// If edge u-v is a valid next edge
if (isValidNextEdge(u, v)) {
System.out.print(u + "-" + v + " ");
// This edge is used so remove it now
removeEdge(u, v);
printEulerUtil(v);
}
}
}
// The function to check if edge u-v can be
// considered as next edge in Euler Tout
private boolean isValidNextEdge(Integer u, Integer v)
{
// The edge u-v is valid in one of the
// following two cases:
// 1) If v is the only adjacent vertex of u
// ie size of adjacent vertex list is 1
if (adj[u].size() == 1) {
return true;
}
// 2) If there are multiple adjacents, then
// u-v is not a bridge Do following steps
// to check if u-v is a bridge
// 2.a) count of vertices reachable from u
boolean[] isVisited = new boolean[this.vertices];
int count1 = dfsCount(u, isVisited);
// 2.b) Remove edge (u, v) and after removing
// the edge, count vertices reachable from u
removeEdge(u, v);
isVisited = new boolean[this.vertices];
int count2 = dfsCount(u, isVisited);
// 2.c) Add the edge back to the graph
addEdge(u, v);
return (count1 > count2) ? false : true;
}
// A DFS based function to count reachable
// vertices from v
private int dfsCount(Integer v, boolean[] isVisited)
{
// Mark the current node as visited
isVisited[v] = true;
int count = 1;
// Recur for all vertices adjacent to this vertex
for (int adj : adj[v]) {
if (!isVisited[adj]) {
count = count + dfsCount(adj, isVisited);
}
}
return count;
}
// Driver program to test above function
public static void main(String a[])
{
// Let us first create and test
// graphs shown in above figure
Graph g1 = new Graph(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
}
}
// This code is contributed by Himanshu Shekhar
Python3
# Python program print Eulerian Trail in a given Eulerian or Semi-Eulerian Graph
from collections import defaultdict
#This class represents an undirected graph using adjacency list representation
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
self.Time = 0
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
self.graph[v].append(u)
# This function removes edge u-v from graph
def rmvEdge(self, u, v):
for index, key in enumerate(self.graph[u]):
if key == v:
self.graph[u].pop(index)
for index, key in enumerate(self.graph[v]):
if key == u:
self.graph[v].pop(index)
# A DFS based function to count reachable vertices from v
def DFSCount(self, v, visited):
count = 1
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
count = count + self.DFSCount(i, visited)
return count
# The function to check if edge u-v can be considered as next edge in
# Euler Tour
def isValidNextEdge(self, u, v):
# The edge u-v is valid in one of the following two cases:
# 1) If v is the only adjacent vertex of u
if len(self.graph[u]) == 1:
return True
else:
'''
2) If there are multiple adjacents, then u-v is not a bridge
Do following steps to check if u-v is a bridge
2.a) count of vertices reachable from u'''
visited =[False]*(self.V)
count1 = self.DFSCount(u, visited)
'''2.b) Remove edge (u, v) and after removing the edge, count
vertices reachable from u'''
self.rmvEdge(u, v)
visited =[False]*(self.V)
count2 = self.DFSCount(u, visited)
#2.c) Add the edge back to the graph
self.addEdge(u,v)
# 2.d) If count1 is greater, then edge (u, v) is a bridge
return False if count1 > count2 else True
# Print Euler tour starting from vertex u
def printEulerUtil(self, u):
#Recur for all the vertices adjacent to this vertex
for v in self.graph[u]:
#If edge u-v is not removed and it's a a valid next edge
if self.isValidNextEdge(u, v):
print("%d-%d " %(u,v)),
self.rmvEdge(u, v)
self.printEulerUtil(v)
'''The main function that print Eulerian Trail. It first finds an odd
degree vertex (if there is any) and then calls printEulerUtil()
to print the path '''
def printEulerTour(self):
#Find a vertex with odd degree
u = 0
for i in range(self.V):
if len(self.graph[i]) %2 != 0 :
u = i
break
# Print tour starting from odd vertex
print ("\n")
self.printEulerUtil(u)
# Create a graph given in the above diagram
g1 = Graph(4)
g1.addEdge(0, 1)
g1.addEdge(0, 2)
g1.addEdge(1, 2)
g1.addEdge(2, 3)
g1.printEulerTour()
g2 = Graph(3)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 0)
g2.printEulerTour()
g3 = Graph (5)
g3.addEdge(1, 0)
g3.addEdge(0, 2)
g3.addEdge(2, 1)
g3.addEdge(0, 3)
g3.addEdge(3, 4)
g3.addEdge(3, 2)
g3.addEdge(3, 1)
g3.addEdge(2, 4)
g3.printEulerTour()
#This code is contributed by Neelam Yadav
C#
// A C# program print Eulerian Trail
// in a given Eulerian or Semi-Eulerian Graph
using System;
using System.Collections.Generic;
// An Undirected graph using
// adjacency list representation
class Graph
{
private int vertices; // No. of vertices
private List<int>[] adj; // adjacency list
// Constructor
Graph(int numOfVertices)
{
// initialise vertex count
this.vertices = numOfVertices;
// initialise adjacency list
initGraph();
}
// utility method to initialise adjacency list
private void initGraph()
{
adj = new List<int>[vertices];
for (int i = 0; i < vertices; i++)
{
adj[i] = new List<int>();
}
}
// add edge u-v
private void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
// This function removes edge u-v from graph.
private void removeEdge(int u, int v)
{
adj[u].Remove(v);
adj[v].Remove(u);
}
/* The main function that print Eulerian Trail.
It first finds an odd degree vertex (if there
is any) and then calls printEulerUtil() to
print the path */
private void printEulerTour()
{
// Find a vertex with odd degree
int u = 0;
for (int i = 0; i < vertices; i++)
{
if (adj[i].Count % 2 == 1)
{
u = i;
break;
}
}
// Print tour starting from oddv
printEulerUtil(u);
Console.WriteLine();
}
// Print Euler tour starting from vertex u
private void printEulerUtil(int u)
{
// Recur for all the vertices
// adjacent to this vertex
for (int i = 0; i < adj[u].Count; i++)
{
int v = adj[u][i];
// If edge u-v is a valid next edge
if (isValidNextEdge(u, v))
{
Console.Write(u + "-" + v + " ");
// This edge is used so remove it now
removeEdge(u, v);
printEulerUtil(v);
}
}
}
// The function to check if edge u-v can be
// considered as next edge in Euler Tout
private bool isValidNextEdge(int u, int v)
{
// The edge u-v is valid in one of the
// following two cases:
// 1) If v is the only adjacent vertex of u
// ie size of adjacent vertex list is 1
if (adj[u].Count == 1)
{
return true;
}
// 2) If there are multiple adjacents, then
// u-v is not a bridge Do following steps
// to check if u-v is a bridge
// 2.a) count of vertices reachable from u
bool[] isVisited = new bool[this.vertices];
int count1 = dfsCount(u, isVisited);
// 2.b) Remove edge (u, v) and after removing
// the edge, count vertices reachable from u
removeEdge(u, v);
isVisited = new bool[this.vertices];
int count2 = dfsCount(u, isVisited);
// 2.c) Add the edge back to the graph
addEdge(u, v);
return (count1 > count2) ? false : true;
}
// A DFS based function to count reachable
// vertices from v
private int dfsCount(int v, bool[] isVisited)
{
// Mark the current node as visited
isVisited[v] = true;
int count = 1;
// Recur for all vertices adjacent
// to this vertex
foreach(int i in adj[v])
{
if (!isVisited[i])
{
count = count + dfsCount(i, isVisited);
}
}
return count;
}
// Driver Code
public static void Main(String []a)
{
// Let us first create and test
// graphs shown in above figure
Graph g1 = new Graph(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
}
}
// This code is contributed by PrinciRaj1992
2-0 0-1 1-2 2-3 0-1 1-2 2-0 0-1 1-2 2-0 0-3 3-4 4-2 2-3 3-1
Tenga en cuenta que el código anterior modifica el gráfico dado, podemos crear una copia del gráfico si no queremos que se modifique el gráfico dado.
Complejidad de tiempo: La complejidad de tiempo de la implementación anterior es O ((V+E) 2 ). La función printEulerUtil() es como DFS y llama a isValidNextEdge() que también hace DFS dos veces. La complejidad temporal de DFS para la representación de listas de adyacencia es O(V+E). Por lo tanto, la complejidad temporal total es O((V+E)*(V+E)) que se puede escribir como O(E 2 ) para un gráfico conexo.
Hay mejores algoritmos para imprimir el recorrido de Euler, el algoritmo de Hierholzer encuentra en el tiempo O (V + E).
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA