Dado un gráfico dirigido ponderado donde los pesos pueden ser negativos, encuentre el camino más corto entre cada par de vértices en el gráfico utilizando el algoritmo de Johnson.
La explicación detallada del algoritmo de Johnson ya se ha comentado en el post anterior .
Consulte : Algoritmo de Johnson para los caminos más cortos de todos los pares .
Esta publicación se enfoca en la implementación del Algoritmo de Johnson.
Algoritmo:
- Sea G el gráfico dado. Agregue un nuevo vértice s al gráfico, agregue aristas desde el nuevo vértice a todos los vértices de G. Sea G’ el gráfico modificado.
- Ejecute el algoritmo Bellman-Ford en G’ con s como fuente. Sean las distancias calculadas por Bellman-Ford h[0], h[1], .. h[V-1]. Si encontramos un ciclo de peso negativo, entonces regresa. Tenga en cuenta que el ciclo de peso negativo no puede ser creado por nuevos vértices ya que no hay borde en s. Todos los bordes son del s.
- Vuelva a ponderar los bordes del gráfico original. Para cada borde (u, v), asigne el nuevo peso como “peso original + h[u] – h[v]”.
- Elimine los vértices agregados y ejecute el algoritmo de Dijkstra para cada vértice.
Ejemplo:
Consideremos el siguiente gráfico.
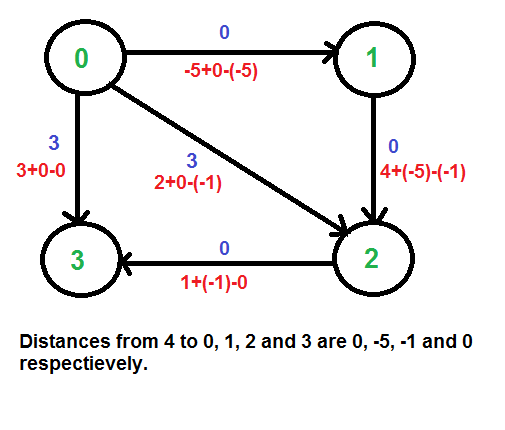
Agregamos una fuente s y agregamos bordes desde s a todos los vértices del gráfico original. En el siguiente diagrama s es 4.
Calculamos las distancias más cortas de 4 a todos los demás vértices usando el algoritmo Bellman-Ford. Las distancias más cortas de 4 a 0, 1, 2 y 3 son 0, -5, -1 y 0 respectivamente, es decir, h[] = {0, -5, -1, 0}. Una vez que obtengamos estas distancias, eliminamos el vértice de origen 4 y volvemos a ponderar los bordes usando la siguiente fórmula. w(u, v) = w(u, v) + h[u] – h[v].
Dado que todos los pesos son positivos ahora, podemos ejecutar el algoritmo de ruta más corta de Dijkstra para cada vértice como fuente.
A continuación se muestra la implementación del enfoque anterior.
# Implementation of Johnson's algorithm in Python3
# Import function to initialize the dictionary
from collections import defaultdict
MAX_INT = float('Inf')
# Returns the vertex with minimum
# distance from the source
def minDistance(dist, visited):
(minimum, minVertex) = (MAX_INT, 0)
for vertex in range(len(dist)):
if minimum > dist[vertex] and visited[vertex] == False:
(minimum, minVertex) = (dist[vertex], vertex)
return minVertex
# Dijkstra Algorithm for Modified
# Graph (removing negative weights)
def Dijkstra(graph, modifiedGraph, src):
# Number of vertices in the graph
num_vertices = len(graph)
# Dictionary to check if given vertex is
# already included in the shortest path tree
sptSet = defaultdict(lambda : False)
# Shortest distance of all vertices from the source
dist = [MAX_INT] * num_vertices
dist[src] = 0
for count in range(num_vertices):
# The current vertex which is at min Distance
# from the source and not yet included in the
# shortest path tree
curVertex = minDistance(dist, sptSet)
sptSet[curVertex] = True
for vertex in range(num_vertices):
if ((sptSet[vertex] == False) and
(dist[vertex] > (dist[curVertex] +
modifiedGraph[curVertex][vertex])) and
(graph[curVertex][vertex] != 0)):
dist[vertex] = (dist[curVertex] +
modifiedGraph[curVertex][vertex]);
# Print the Shortest distance from the source
for vertex in range(num_vertices):
print ('Vertex ' + str(vertex) + ': ' + str(dist[vertex]))
# Function to calculate shortest distances from source
# to all other vertices using Bellman-Ford algorithm
def BellmanFord(edges, graph, num_vertices):
# Add a source s and calculate its min
# distance from every other node
dist = [MAX_INT] * (num_vertices + 1)
dist[num_vertices] = 0
for i in range(num_vertices):
edges.append([num_vertices, i, 0])
for i in range(num_vertices):
for (src, des, weight) in edges:
if((dist[src] != MAX_INT) and
(dist[src] + weight < dist[des])):
dist[des] = dist[src] + weight
# Don't send the value for the source added
return dist[0:num_vertices]
# Function to implement Johnson Algorithm
def JohnsonAlgorithm(graph):
edges = []
# Create a list of edges for Bellman-Ford Algorithm
for i in range(len(graph)):
for j in range(len(graph[i])):
if graph[i][j] != 0:
edges.append([i, j, graph[i][j]])
# Weights used to modify the original weights
modifyWeights = BellmanFord(edges, graph, len(graph))
modifiedGraph = [[0 for x in range(len(graph))] for y in
range(len(graph))]
# Modify the weights to get rid of negative weights
for i in range(len(graph)):
for j in range(len(graph[i])):
if graph[i][j] != 0:
modifiedGraph[i][j] = (graph[i][j] +
modifyWeights[i] - modifyWeights[j]);
print ('Modified Graph: ' + str(modifiedGraph))
# Run Dijkstra for every vertex as source one by one
for src in range(len(graph)):
print ('\nShortest Distance with vertex ' +
str(src) + ' as the source:\n')
Dijkstra(graph, modifiedGraph, src)
# Driver Code
graph = [[0, -5, 2, 3],
[0, 0, 4, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]]
JohnsonAlgorithm(graph)
Modified Graph: [[0, 0, 3, 3], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]] Shortest Distance with vertex 0 as the source: Vertex 0: 0 Vertex 1: 0 Vertex 2: 0 Vertex 3: 0 Shortest Distance with vertex 1 as the source: Vertex 0: inf Vertex 1: 0 Vertex 2: 0 Vertex 3: 0 Shortest Distance with vertex 2 as the source: Vertex 0: inf Vertex 1: inf Vertex 2: 0 Vertex 3: 0 Shortest Distance with vertex 3 as the source: Vertex 0: inf Vertex 1: inf Vertex 2: inf Vertex 3: 0
Complejidad de tiempo: la complejidad de tiempo del algoritmo anterior es 
la que toma el algoritmo de Dijkstra 
para la array de adyacencia. Tenga en cuenta que el algoritmo anterior se puede hacer más eficiente mediante el uso de la lista de adyacencia en lugar de la array de adyacencia para representar el Gráfico.
Publicación traducida automáticamente
Artículo escrito por rituraj_jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA