La ordenación topológica para un gráfico cíclico dirigido ( DAG ) es una ordenación lineal de vértices tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. La clasificación topológica de un gráfico no es posible si el gráfico no es un DAG.
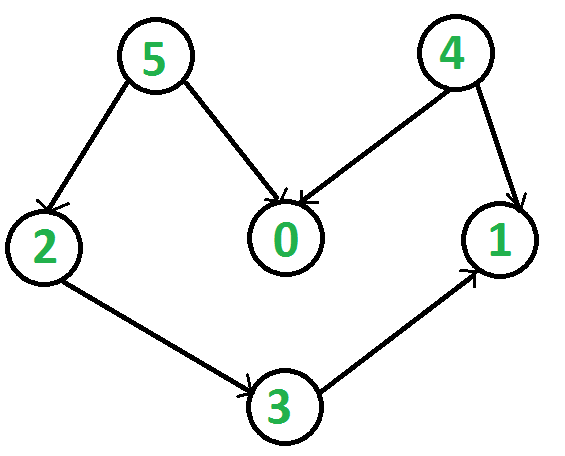
Por ejemplo, una ordenación topológica del siguiente gráfico es “5 4 2 3 1 0?. Puede haber más de una clasificación topológica para un gráfico. Por ejemplo, otra ordenación topológica del siguiente gráfico es “4 5 2 0 3 1″. El primer vértice en la clasificación topológica siempre es un vértice con un grado de entrada de 0 (un vértice sin bordes entrantes).
Veamos algunos ejemplos con la explicación adecuada,
Ejemplo:
Aporte:
Salida: 5 4 2 3 1 0
Explicación: la ordenación topológica de un DAG se realiza en un orden tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. 5 no tiene borde entrante. 4 no tiene borde entrante, 2 y 0 tienen borde entrante de 4 y 5 y 1 se coloca al final.
Aporte:
Salida: 0 3 4 1 2
Explicación: 0 y 3 no tienen borde entrante, 4 y 1 tienen borde entrante desde 0 y 3. 2 se coloca al final.
Ya se ha discutido una solución basada en DFS para encontrar una ordenación topológica .
Solución : en este artículo, veremos otra forma de encontrar el orden lineal de los vértices en un gráfico acíclico dirigido (DAG). El enfoque se basa en el siguiente hecho:
un DAG G tiene al menos un vértice con grado de entrada 0 y un vértice con grado de salida 0 .
Prueba: hay una prueba simple del hecho anterior de que un DAG no contiene un ciclo, lo que significa que todas las rutas tendrán una longitud finita. Ahora sea S el camino más largo desde u (origen) hasta v (destino). Dado que S es el camino más largo, no puede haber un borde de entrada a u ni un borde de salida de v, si esta situación hubiera ocurrido, entonces S no habría sido el camino más largo
=> grado interior(u) = 0 y grado exterior(v) = 0
Intuición:
La clasificación topológica es un tipo de problema de dependencias, por lo que podemos comenzar con las tareas que no tienen dependencias y se pueden realizar de inmediato o simplemente si hablamos en el término de Node,
- Siempre intentaremos ejecutar aquellos Nodes que tengan un grado superior a 0.
- Luego, después de la ejecución de todos esos 0 grados externos, ejecutaremos los que dependen directamente de las tareas resueltas actualmente (los grados externos de las tareas resueltas actualmente se convertirán en 0 ahora) y así sucesivamente ejecutará todas las demás tareas.
Observamos de cerca que estamos haciendo que estas ejecuciones se realicen por niveles o en una forma de búsqueda de amplitud (BFS). Del mismo modo, también podemos realizar la misma tarea para indegree=0.
Algoritmo: Pasos necesarios para encontrar el orden topológico de un DAG:
Paso 1: Calcule el grado de entrada (número de aristas entrantes) para cada uno de los vértices presentes en el DAG e inicialice el recuento de Nodes visitados como 0.
Paso 2: Elija todos los vértices con grado de entrada 0 y agréguelos a una cola (operación de puesta en cola)
Paso 3: elimine un vértice de la cola (operación de eliminación de cola) y luego.
- Incremente el recuento de Nodes visitados en 1.
- Disminuya el grado en 1 para todos sus Nodes vecinos.
- Si el grado de entrada de los Nodes vecinos se reduce a cero, agréguelo a la cola.
Paso 4: repita el paso 3 hasta que la cola esté vacía.
Paso 5: si el recuento de Nodes visitados no es igual al número de Nodes en el gráfico, entonces la ordenación topológica no es posible para el gráfico dado.
¿Cómo encontrar el grado de entrada de cada Node?
Hay 2 formas de calcular el grado de cada vértice:
- Tome una array en grados que realizará un seguimiento de
Atraviesa la array de bordes y simplemente aumente el contador del Node de destino en 1.
for each node in Nodes
indegree[node] = 0;
for each edge(src, dest) in Edges
indegree[dest]++
- Complejidad temporal: O(V+E)
- Recorra la lista para cada Node y luego incremente el grado de entrada de todos los Nodes conectados a él en 1.
for each node in Nodes
If (list[node].size()!=0) then
for each dest in list
indegree[dest]++;
- Complejidad de tiempo: el bucle for externo se ejecutará V número de veces y el bucle for interno se ejecutará E número de veces. Por lo tanto, la complejidad de tiempo general es O (V + E).
La complejidad temporal general del algoritmo es O(V+E)
A continuación se muestra la implementación del algoritmo anterior. La implementación usa el método 2 discutido anteriormente para encontrar en grados.
C++
// A C++ program to print topological
// sorting of a graph using indegrees.
#include <bits/stdc++.h>
using namespace std;
// Class to represent a graph
class Graph {
// No. of vertices'
int V;
// Pointer to an array containing
// adjacency listsList
list<int>* adj;
public:
// Constructor
Graph(int V);
// Function to add an edge to graph
void addEdge(int u, int v);
// prints a Topological Sort of
// the complete graph
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int u, int v)
{
adj[u].push_back(v);
}
// The function to do
// Topological Sort.
void Graph::topologicalSort()
{
// Create a vector to store
// indegrees of all
// vertices. Initialize all
// indegrees as 0.
vector<int> in_degree(V, 0);
// Traverse adjacency lists
// to fill indegrees of
// vertices. This step
// takes O(V+E) time
for (int u = 0; u < V; u++) {
list<int>::iterator itr;
for (itr = adj[u].begin();
itr != adj[u].end(); itr++)
in_degree[*itr]++;
}
// Create an queue and enqueue
// all vertices with indegree 0
queue<int> q;
for (int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.push(i);
// Initialize count of visited vertices
int cnt = 0;
// Create a vector to store
// result (A topological
// ordering of the vertices)
vector<int> top_order;
// One by one dequeue vertices
// from queue and enqueue
// adjacents if indegree of
// adjacent becomes 0
while (!q.empty()) {
// Extract front of queue
// (or perform dequeue)
// and add it to topological order
int u = q.front();
q.pop();
top_order.push_back(u);
// Iterate through all its
// neighbouring nodes
// of dequeued node u and
// decrease their in-degree
// by 1
list<int>::iterator itr;
for (itr = adj[u].begin();
itr != adj[u].end(); itr++)
// If in-degree becomes zero,
// add it to queue
if (--in_degree[*itr] == 0)
q.push(*itr);
cnt++;
}
// Check if there was a cycle
if (cnt != V) {
cout << "There exists a cycle in the graph\n";
return;
}
// Print topological order
for (int i = 0; i < top_order.size(); i++)
cout << top_order[i] << " ";
cout << endl;
}
// Driver program to test above functions
int main()
{
// Create a graph given in the
// above diagram
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort of\n";
g.topologicalSort();
return 0;
}
Java
// A Java program to print topological
// sorting of a graph using indegrees
import java.util.*;
// Class to represent a graph
class Graph {
// No. of vertices
int V;
// An Array of List which contains
// references to the Adjacency List of
// each vertex
List<Integer> adj[];
// Constructor
public Graph(int V)
{
this.V = V;
adj = new ArrayList[V];
for (int i = 0; i < V; i++)
adj[i] = new ArrayList<Integer>();
}
// Function to add an edge to graph
public void addEdge(int u, int v)
{
adj[u].add(v);
}
// prints a Topological Sort of the
// complete graph
public void topologicalSort()
{
// Create a array to store
// indegrees of all
// vertices. Initialize all
// indegrees as 0.
int indegree[] = new int[V];
// Traverse adjacency lists
// to fill indegrees of
// vertices. This step takes
// O(V+E) time
for (int i = 0; i < V; i++) {
ArrayList<Integer> temp
= (ArrayList<Integer>)adj[i];
for (int node : temp) {
indegree[node]++;
}
}
// Create a queue and enqueue
// all vertices with indegree 0
Queue<Integer> q
= new LinkedList<Integer>();
for (int i = 0; i < V; i++) {
if (indegree[i] == 0)
q.add(i);
}
// Initialize count of visited vertices
int cnt = 0;
// Create a vector to store result
// (A topological ordering of the vertices)
Vector<Integer> topOrder = new Vector<Integer>();
while (!q.isEmpty()) {
// Extract front of queue
// (or perform dequeue)
// and add it to topological order
int u = q.poll();
topOrder.add(u);
// Iterate through all its
// neighbouring nodes
// of dequeued node u and
// decrease their in-degree
// by 1
for (int node : adj[u]) {
// If in-degree becomes zero,
// add it to queue
if (--indegree[node] == 0)
q.add(node);
}
cnt++;
}
// Check if there was a cycle
if (cnt != V) {
System.out.println(
"There exists a cycle in the graph");
return;
}
// Print topological order
for (int i : topOrder) {
System.out.print(i + " ");
}
}
}
// Driver program to test above functions
class Main {
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
System.out.println(
"Following is a Topological Sort");
g.topologicalSort();
}
}
Python3
# A Python program to print topological sorting of a graph
# using indegrees
from collections import defaultdict
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list) # dictionary containing adjacency List
self.V = vertices # No. of vertices
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# The function to do Topological Sort.
def topologicalSort(self):
# Create a vector to store indegrees of all
# vertices. Initialize all indegrees as 0.
in_degree = [0]*(self.V)
# Traverse adjacency lists to fill indegrees of
# vertices. This step takes O(V + E) time
for i in self.graph:
for j in self.graph[i]:
in_degree[j] += 1
# Create an queue and enqueue all vertices with
# indegree 0
queue = []
for i in range(self.V):
if in_degree[i] == 0:
queue.append(i)
# Initialize count of visited vertices
cnt = 0
# Create a vector to store result (A topological
# ordering of the vertices)
top_order = []
# One by one dequeue vertices from queue and enqueue
# adjacents if indegree of adjacent becomes 0
while queue:
# Extract front of queue (or perform dequeue)
# and add it to topological order
u = queue.pop(0)
top_order.append(u)
# Iterate through all neighbouring nodes
# of dequeued node u and decrease their in-degree
# by 1
for i in self.graph[u]:
in_degree[i] -= 1
# If in-degree becomes zero, add it to queue
if in_degree[i] == 0:
queue.append(i)
cnt += 1
# Check if there was a cycle
if cnt != self.V:
print ("There exists a cycle in the graph")
else :
# Print topological order
print (top_order)
g = Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print ("Following is a Topological Sort of the given graph")
g.topologicalSort()
# This code is contributed by Neelam Yadav
C#
// C# program to print topological
// sorting of a graph using indegrees.
using System;
using System.Collections.Generic;
// Class to represent a graph
public class Graph {
// No. of vertices'
private int V;
// Pointer to an array containing
// adjacency listsList
private List<int>[] adj;
// Constructor
public Graph(int V)
{
this.V = V;
adj = new List<int>[ V ];
for (int i = 0; i < V; i++)
adj[i] = new List<int>();
}
// Function to Add an edge to graph
public void AddEdge(int u, int v) { adj[u].Add(v); }
// The function to do Topological Sort.
public void TopologicalSort()
{
// Create a list to store
// indegrees of all
// vertices. Initialize all
// indegrees as 0.
int[] in_degree = new int[V];
// Traverse adjacency lists
// to fill indegrees of
// vertices. This step
// takes O(V+E) time
for (int u = 0; u < V; u++) {
foreach(int itr in adj[u]) in_degree[itr]++;
}
// Create an queue and enqueue
// all vertices with indegree 0
Queue<int> q = new Queue<int>();
for (int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.Enqueue(i);
// Initialize count of visited vertices
int cnt = 0;
// Create a vector to store
// result (A topological
// ordering of the vertices)
List<int> top_order = new List<int>();
// One by one dequeue vertices
// from queue and enqueue
// adjacents if indegree of
// adjacent becomes 0
while (q.Count > 0)
{
// Extract front of queue
// (or perform dequeue)
// and Add it to topological order
int u = q.Dequeue();
top_order.Add(u);
// Iterate through all its
// neighbouring nodes
// of dequeued node u and
// decrease their in-degree
// by 1
foreach(int itr in adj[u])
{
// If in-degree becomes zero,
// Add it to queue
if (--in_degree[itr] == 0)
q.Enqueue(itr);
}
cnt++;
}
// Check if there was a cycle
if (cnt != V) {
Console.WriteLine(
"There exists a cycle in the graph");
return;
}
// Print topological order
for (int i = 0; i < top_order.Count; i++)
Console.Write(top_order[i] + " ");
Console.WriteLine();
}
}
// Driver program to test above functions
public class GFG {
static void Main(string[] args)
{
// Create a graph given in the
// above diagram
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine(
"Following is a Topological Sort of");
g.TopologicalSort();
}
}
// This code is contributed by cavi4762.
Javascript
<script>
// A Javascript program to print topological
// sorting of a graph using indegrees
// No. of vertices
let V;
// An Array of List which contains
// references to the Adjacency List of
// each vertex
let adj;
function Graph(v)
{
V = v;
adj = new Array(V);
for (let i = 0; i < V; i++)
adj[i] = [];
}
// Function to add an edge to graph
function addEdge(u, v)
{
adj[u].push(v);
}
// prints a Topological Sort of the
// complete graph
function topologicalSort()
{
// Create a array to store
// indegrees of all
// vertices. Initialize all
// indegrees as 0.
let indegree = new Array(V);
for(let i = 0; i < V; i++)
indegree[i] = 0;
// Traverse adjacency lists
// to fill indegrees of
// vertices. This step takes
// O(V+E) time
for (let i = 0; i < V; i++) {
let temp
= adj[i];
for (let node = 0; node < temp.length; node++) {
indegree[temp[node]]++;
}
}
// Create a queue and enqueue
// all vertices with indegree 0
let q = [];
for (let i = 0; i < V; i++) {
if (indegree[i] == 0)
q.push(i);
}
// Initialize count of visited vertices
let cnt = 0;
// Create a vector to store result
// (A topological ordering of the vertices)
let topOrder = [];
while (q.length!=0)
{
// Extract front of queue
// (or perform dequeue)
// and add it to topological order
let u = q.shift();
topOrder.push(u);
// Iterate through all its
// neighbouring nodes
// of dequeued node u and
// decrease their in-degree
// by 1
for (let node = 0; node < adj[u].length; node++)
{
// If in-degree becomes zero,
// add it to queue
if (--indegree[adj[u][node]] == 0)
q.push(adj[u][node]);
}
cnt++;
}
// Check if there was a cycle
if (cnt != V) {
document.write(
"There exists a cycle in the graph");
return;
}
// Print topological order
for (let i = 0; i < topOrder.length; i++)
{
document.write(topOrder[i] + " ");
}
}
// Driver program to test above functions
// Create a graph given in the above diagram
Graph(6);
addEdge(5, 2);
addEdge(5, 0);
addEdge(4, 0);
addEdge(4, 1);
addEdge(2, 3);
addEdge(3, 1);
document.write(
"Following is a Topological Sort<br>");
topologicalSort();
// This code is contributed by avanitrachhadiya2155
</script>
Following is a Topological Sort of 4 5 2 0 3 1
Análisis de Complejidad:
- Complejidad Temporal: O(V+E).
El bucle for externo se ejecutará V número de veces y el bucle for interno se ejecutará E número de veces. - Espacio Auxiliar: O(V).
La cola necesita almacenar todos los vértices del gráfico. Entonces el espacio requerido es O(V)
Este artículo es una contribución de Chirag Agarwal . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

