Dado un gráfico no dirigido y no ponderado, encuentre el corte más pequeño (el menor número de aristas que desconecta el gráfico en dos componentes).
El gráfico de entrada puede tener bordes paralelos.
Por ejemplo, considere el siguiente ejemplo, el corte más pequeño tiene 2 bordes.
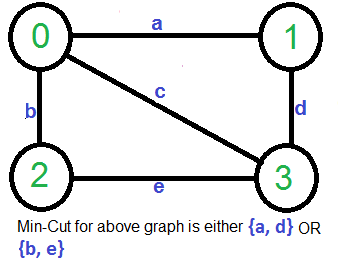
Una solución simple utiliza el algoritmo de corte s-t basado en Max-Flow para encontrar el corte mínimo. Considere cada par de vértices como fuente ‘s’ y sumidero ‘t’, y llame al algoritmo de corte de st mínimo para encontrar el corte de st. Vuelva al mínimo de todos los cortes de st. La mejor complejidad temporal posible de este algoritmo es O(V 5 ) para un gráfico. [¿Cómo? hay un total de V 2 pares posibles y el algoritmo de corte st para un par toma el tiempo O(V*E) y E = O(V 2 )].
A continuación se muestra el algoritmo de Karger simple para este propósito. A continuación, el algoritmo de Karger se puede implementar en el tiempo O(E) = O(V 2 ).
1) Initialize contracted graph CG as copy of original graph
2) While there are more than 2 vertices.
a) Pick a random edge (u, v) in the contracted graph.
b) Merge (or contract) u and v into a single vertex (update
the contracted graph).
c) Remove self-loops
3) Return cut represented by two vertices.
Entendamos el algoritmo anterior a través del ejemplo dado.
Deje que el primer vértice elegido al azar sea ‘ a ‘ que conecta los vértices 0 y 1. Eliminamos este borde y contraemos el gráfico (combinamos los vértices 0 y 1). Obtenemos el siguiente gráfico.
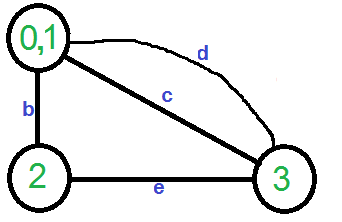
Deje que el siguiente borde elegido al azar sea ‘d’. Eliminamos este borde y combinamos los vértices (0,1) y 3.
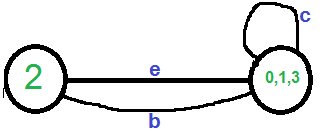
Necesitamos eliminar los bucles automáticos en el gráfico. Entonces eliminamos el borde ‘c’
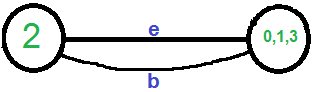
Ahora el gráfico tiene dos vértices, así que nos detenemos. El número de aristas en el gráfico resultante es el corte producido por el algoritmo de Karger.
El algoritmo de Karger es un algoritmo de Monte Carlo y el corte producido por él puede no ser mínimo. Por ejemplo, el siguiente diagrama muestra que un orden diferente de selección de bordes aleatorios produce un corte mínimo de tamaño 3.
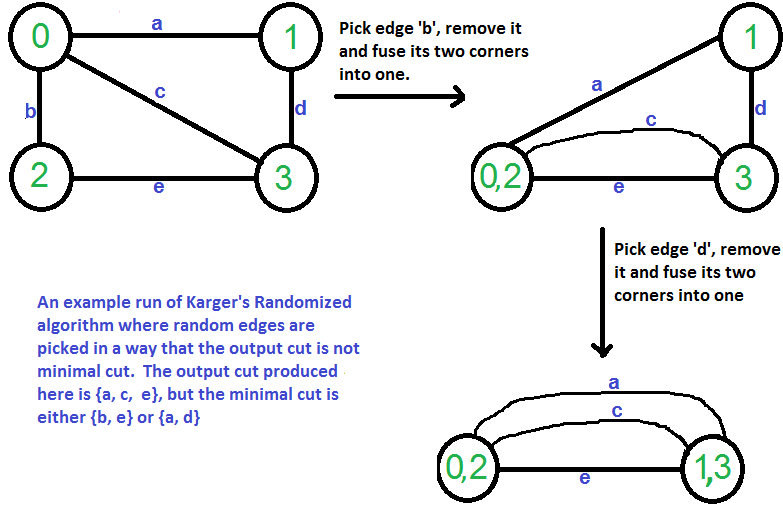
A continuación se muestra la implementación en C++ del algoritmo anterior. El gráfico de entrada se representa como una colección de aristas y la estructura de datos de búsqueda de unión se utiliza para realizar un seguimiento de los componentes.
C++
// Karger's algorithm to find Minimum Cut in an
// undirected, unweighted and connected graph.
#include <iostream>
//#include <stdlib.h>
#include <time.h>
// a structure to represent a unweighted edge in graph
struct Edge
{
int src, dest;
};
// a structure to represent a connected, undirected
// and unweighted graph as a collection of edges.
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
Edge* edge;
};
// A structure to represent a subset for union-find
struct subset
{
int parent;
int rank;
};
// Function prototypes for union-find (These functions are defined
// after kargerMinCut() )
int find(struct subset subsets[], int i);
void Union(struct subset subsets[], int x, int y);
// A very basic implementation of Karger's randomized
// algorithm for finding the minimum cut. Please note
// that Karger's algorithm is a Monte Carlo Randomized algo
// and the cut returned by the algorithm may not be
// minimum always
int kargerMinCut(struct Graph* graph)
{
// Get data of given graph
int V = graph->V, E = graph->E;
Edge *edge = graph->edge;
// Allocate memory for creating V subsets.
struct subset *subsets = new subset[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
// Initially there are V vertices in
// contracted graph
int vertices = V;
// Keep contracting vertices until there are
// 2 vertices.
while (vertices > 2)
{
// Pick a random edge
int i = rand() % E;
// Find vertices (or sets) of two corners
// of current edge
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
// If two corners belong to same subset,
// then no point considering this edge
if (subset1 == subset2)
continue;
// Else contract the edge (or combine the
// corners of edge into one vertex)
else
{
printf("Contracting edge %d-%d\n",
edge[i].src, edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
// Now we have two vertices (or subsets) left in
// the contracted graph, so count the edges between
// two components and return the count.
int cutedges = 0;
for (int i=0; i<E; i++)
{
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
if (subset1 != subset2)
cutedges++;
}
return cutedges;
}
// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i)
subsets[i].parent =
find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root and
// increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
// Driver program to test above functions
int main()
{
/* Let us create following unweighted graph
0------1
| \ |
| \ |
| \|
2------3 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
// add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
// add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
// add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
// Use a different seed value for every run.
srand(time(NULL));
printf("\nCut found by Karger's randomized algo is %d\n",
kargerMinCut(graph));
return 0;
}
Java
//Java program to implement the Karger's algorithm to find Minimum Cut in an
// undirected, unweighted and connected graph.
import java.io.*;
import java.util.*;
class GFG {
// a structure to represent a unweighted edge in graph
public static class Edge
{
int src, dest;
Edge(int s, int d){
this.src = s;
this.dest = d;
}
}
// a structure to represent a connected, undirected
// and unweighted graph as a collection of edges.
public static class Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
Edge edge[];
Graph(int v, int e){
this.V = v;
this.E = e;
this.edge = new Edge[e];
/*for(int i=0;i<e;i++){
this.edge[i]=new Edge(-1,-1);
}*/
}
}
// A structure to represent a subset for union-find
public static class subset
{
int parent;
int rank;
subset(int p, int r){
this.parent = p;
this.rank = r;
}
}
// A very basic implementation of Karger's randomized
// algorithm for finding the minimum cut. Please note
// that Karger's algorithm is a Monte Carlo Randomized algo
// and the cut returned by the algorithm may not be
// minimum always
public static int kargerMinCut(Graph graph)
{
// Get data of given graph
int V = graph.V, E = graph.E;
Edge edge[] = graph.edge;
// Allocate memory for creating V subsets.
subset subsets[] = new subset[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v] = new subset(v,0);
}
// Initially there are V vertices in
// contracted graph
int vertices = V;
// Keep contracting vertices until there are
// 2 vertices.
while (vertices > 2)
{
// Pick a random edge
int i = ((int)(Math.random()*10)) % E;
// Find vertices (or sets) of two corners
// of current edge
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
// If two corners belong to same subset,
// then no point considering this edge
if (subset1 == subset2){
continue;
}
// Else contract the edge (or combine the
// corners of edge into one vertex)
else
{
System.out.println("Contracting edge "+edge[i].src+"-"+edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
// Now we have two vertices (or subsets) left in
// the contracted graph, so count the edges between
// two components and return the count.
int cutedges = 0;
for (int i=0; i<E; i++)
{
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
if (subset1 != subset2){
cutedges++;
}
}
return cutedges;
}
// A utility function to find set of an element i
// (uses path compression technique)
public static int find(subset subsets[], int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i){
subsets[i].parent = find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
public static void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank){
subsets[xroot].parent = yroot;
}else{
if (subsets[xroot].rank > subsets[yroot].rank){
subsets[yroot].parent = xroot;
}
// If ranks are same, then make one as root and
// increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
}
// Driver program to test above functions
public static void main (String[] args) {
/* Let us create following unweighted graph
0------1
| \ |
| \ |
| \|
2------3 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
// Creates a graph with V vertices and E edges
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0] = new Edge(0,1);
// add edge 0-2
graph.edge[1] = new Edge(0,2);
// add edge 0-3
graph.edge[2] = new Edge(0,3);
// add edge 1-3
graph.edge[3] = new Edge(1,3);
// add edge 2-3
graph.edge[4] = new Edge(2,3);
System.out.println("Cut found by Karger's randomized algo is "+kargerMinCut(graph));
}
}
//This code is contributed by shruti456rawal
Contracting edge 0-1 Contracting edge 1-3 Cut found by Karger's randomized algo is 2
Tenga en cuenta que el programa anterior se basa en el resultado de una función aleatoria y puede producir un resultado diferente.
En esta publicación, hemos discutido el algoritmo de Karger simple y hemos visto que el algoritmo no siempre produce un corte mínimo. El algoritmo anterior produce un corte mínimo con una probabilidad mayor o igual que 1/(n 2 ). Consulte la próxima publicación sobre Análisis y aplicaciones del algoritmo de Karger , se discuten las aplicaciones, la prueba de esta probabilidad y las mejoras.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA