Algoritmo de Manacher – Substring palindrómica más larga de tiempo lineal – Parte 2

En Algoritmo de Manacher – Parte 1 , revisamos algunos de los conceptos básicos y la array de longitud LPS.
Aquí veremos cómo calcular la array de longitud LPS de manera eficiente.

Para calcular la array LPS de manera eficiente, debemos comprender cómo la longitud LPS para cualquier posición puede relacionarse con el valor de longitud LPS de cualquier posición anterior ya calculada.
Para la string «abaaba», vemos lo siguiente:

Si miramos alrededor de la posición 3:

• El valor de longitud LPS en la posición 2 y la posición 4 es el mismo
• El valor de longitud LPS en la posición 1 y la posición 5 es el mismo

Calculamos los valores de longitud LPS de izquierda a derecha comenzando desde la posición 0, por lo que podemos ver si ya conocemos los valores de longitud LPS en las posiciones 1, 2 y 3, entonces es posible que no necesitemos calcular la longitud LPS en las posiciones 4 y 5 porque son igual a los valores de longitud LPS en las posiciones correspondientes en el lado izquierdo de la posición 3.

Si miramos alrededor de la posición 6:

• El valor de longitud LPS en la posición 5 y la posición 7 es el mismo
• El valor de longitud LPS en la posición 4 y la posición 8 es el mismo

…………. y así.
Si ya conocemos los valores de longitud LPS en las posiciones 1, 2, 3, 4, 5 y 6, es posible que no necesitemos calcular la longitud LPS en las posiciones 7, 8, 9, 10 y 11 porque son iguales a los valores de longitud LPS en posiciones correspondientes en el lado izquierdo de la posición 6.
Para la string «abababa», vemos lo siguiente:

Si ya conocemos los valores de longitud LPS en las posiciones 1, 2, 3, 4, 5, 6 y 7, es posible que no necesitemos calcular la longitud LPS en las posiciones 8, 9, 10, 11, 12 y 13 porque son iguales a Valores de longitud LPS en las posiciones correspondientes en el lado izquierdo de la posición 7.

¿Puedes ver por qué los valores de longitud LPS son simétricos en las posiciones 3, 6, 9 en la string «abaaba»? Eso es porque hay una substring palindrómica alrededor de estas posiciones. Lo mismo ocurre en la string «abababa» alrededor de la posición 7.
¿Es siempre cierto que los valores de longitud LPS alrededor de la posición central palindrómica son siempre simétricos (igual)?
La respuesta es NO.
Mire las posiciones 3 y 11 en la string «abababa». Ambas posiciones tienen LPS de longitud 3. Las posiciones inmediatas izquierda y derecha son simétricas (con valor 0), pero no la siguiente. Las posiciones 1 y 5 (alrededor de la posición 3) no son simétricas. De manera similar, las posiciones 9 y 13 (alrededor de la posición 11) no son simétricas.

En este punto, podemos ver que si hay un palíndromo en una cuerda centrada en alguna posición, entonces los valores de longitud LPS alrededor de la posición central pueden o no ser simétricos dependiendo de alguna situación. Si podemos identificar la situación en la que las posiciones izquierda y derecha SERÁN SIMÉTRICAS alrededor de la posición central, NO NECESITAMOS calcular la longitud LPS de la posición derecha porque será exactamente igual que el valor LPS de la posición correspondiente en el lado izquierdo que ya se conoce. Y este hecho en el que estamos evitando el cálculo de la longitud de LPS en pocas posiciones hace que el algoritmo de Manacher sea lineal.

En situaciones en las que las posiciones izquierda y derecha NO SERÁN SIMÉTRICAS alrededor de la posición central, comparamos los caracteres en el lado izquierdo y derecho para encontrar el palíndromo, pero aquí también el algoritmo intenta evitar ciertas comparaciones. Pronto veremos todos estos escenarios.

Introduzcamos algunos términos para continuar: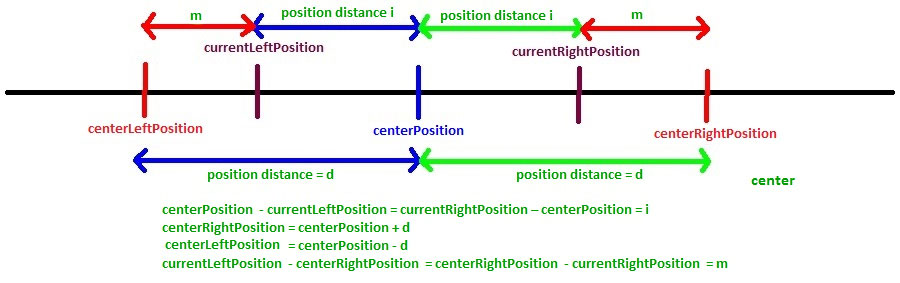

• centerPosition : esta es la posición para la que se calcula la longitud de LPS y digamos que la longitud de LPS en centerPosition es d (es decir, L[centerPosition] = d)
• centerRightPosition : esta es la posición que está a la derecha de centerPosition y la posición d lejos de centerPosition (es decir , centerRightPosition = centerPosition + d )
• centerLeftPosition : esta es la posición que queda en centerPosition y la posición d lejos de centerPosition (es decir , centerLeftPosition = centerPosition – d )
• currentRightPosition : esta es la posición que está a la derecha de centerPosition para la cual la longitud de LPS aún no se conoce y debe calcularse
• currentLeftPosition : esta es la posición en el lado izquierdo de centerPosition que corresponde a currentRightPosition
  centerPosition – currentLeftPosition = currentRightPosition – centerPosition
  currentLeftPosition = 2* centerPosition – currentRightPosition
• i-left palindrome : el palíndromo i se coloca a la izquierda de centerPosition, es decir, en currentLeftPosition
• i-palíndromo derecho : el palíndromo i se coloca a la derecha de centerPosition, es decir, en currentRightPosition
• centro palíndromo – El palíndromo en centerPosition

Cuando estamos en la posición central para la que se conoce la longitud LPS, también conocemos la longitud LPS de todas las posiciones más pequeñas que la posición central. Digamos que la longitud de LPS en posición central es d, es decir,
L[posición central] = d

Significa que la substring entre las posiciones «centerPosition-d» a «centerPosition+d» es un palíndromo.
Ahora procedemos a calcular la longitud LPS de posiciones mayores que centerPosition.
Digamos que estamos en currentRightPosition ( > centerPosition) donde necesitamos encontrar la longitud de LPS.
Para esto, observamos la longitud LPS de currentLeftPosition que ya está calculada.

Si la longitud LPS de currentLeftPosition es menor que “centerRightPosition – currentRightPosition”, entonces la longitud LPS de currentRightPosition será igual a la longitud LPS de currentLeftPosition. Entonces
L[posiciónDerechaActual] = L[posiciónIzquierdaActual] si L[posiciónIzquierdaActual] <posiciónDerechaCentro – posiciónDerechaActual. Este es el Caso 1 .

Consideremos el siguiente escenario para la string «abababa»:

                          (click to see it clearly)
                    

Hemos calculado la longitud LPS hasta la posición 7 donde L[7] = 7, si consideramos la posición 7 como posición central, entonces la posición central izquierda será 0 y la posición central derecha será 14.
Ahora necesitamos calcular la longitud LPS de otras posiciones a la derecha de posición central.

Para currentRightPosition = 8, currentLeftPosition es 6 y L[currentLeftPosition] = 0
También centerRightPosition – currentRightPosition = 14 – 8 = 6 El
caso 1 se aplica aquí y, por lo tanto, L[currentRightPosition] = L[8] = 0 El
caso 1 se aplica a las posiciones 10 y 12 , entonces,
L[10] = L[4] = 0
L[12] = L[2] = 0

Si observamos la posición 9, entonces:
PosiciónDerechaActual = 9 PosiciónIzquierdaActual
= 2* PosiciónCentro – PosiciónDerechaActual = 2*7 – 9 = 5
PosiciónDerechaCentro – PosiciónDerechaActual = 14 – 9 = 5

Aquí L[posiciónIzquierdaActual] = PosiciónDerechaCentro – PosiciónDerechaActual, por lo que el Caso 1 no se aplica aquí. También tenga en cuenta que centerRightPosition es la posición final extrema de la string. Eso significa que el palíndromo central es el sufijo de la string de entrada. En ese caso, L[posiciónDerechaActual] = L[posiciónIzquierdaActual]. Este es el Caso 2 .

El caso 2 se aplica a las posiciones 9, 11, 13 y 14, así:
L[9] = L[5] = 5
L[11] = L[3] = 3
L[13] = L[1] = 1
L[ 14] = L[0] = 0

¿Qué está pasando realmente en el Caso 1 y el Caso 2? Esto solo está utilizando la propiedad simétrica palindrómica y sin ninguna coincidencia de caracteres, está encontrando la longitud LPS de nuevas posiciones.

Cuando un palíndromo de mayor longitud contiene un palíndromo de menor longitud centrado en el lado izquierdo de su propio centro, entonces, según la propiedad simétrica, habrá otro palíndromo más pequeño centrado a la derecha del centro del palíndromo más grande. Si el palíndromo más pequeño del lado izquierdo no es el prefijo del palíndromo más grande, entonces se aplica el Caso 1 y si es un prefijo Y el palíndromo más grande es el sufijo de la string de entrada en sí, entonces se aplica el Caso 2 .

El palíndromo más largo que se coloca a la derecha del centro actual (el palíndromo i-derecho) es tan largo como el palíndromo más largo que se coloca a la izquierda del centro actual (el palíndromo i-izquierdo) si el palíndromo i-izquierdo es completamente contenido en el palíndromo más largo alrededor del centro actual (el palíndromo central) y el palíndromo i-izquierdo no es un prefijo del palíndromo central ( Caso 1 ) o (es decir, cuando el palíndromo i-izquierdo es un prefijo del palíndromo central) si el palíndromo central palíndromo es un sufijo de toda la string ( Caso 2 ).

En el Caso 1 y el Caso 2, el i-right palindrome no puede expandirse más que el i-left palindrome correspondiente (¿puedes visualizar por qué no puede expandirse más?), por lo que la longitud LPS del i-right palindrome es exactamente la misma que la del LPS longitud del palíndromo i-izquierdo.

Aquí, los palíndromos i-izquierdo e i-derecho están completamente contenidos en el palíndromo central (es decir, L[posición izquierda actual] <= posición derecha central – posición derecha actual)
Ahora, si el palíndromo i-izquierda no es un prefijo del palíndromo central (L [posición izquierda actual] < posición derecha central – posición derecha actual ), eso significa que i-left palindrome no pudo expandirse hasta la posición centerLeftPosition.

Si observamos el seguimiento con centerPosition = 11, entonces

                          (click to see it clearly)
                    

centerLeftPosition sería 11 – 9 = 2, y centerRightPosition sería 11 + 9 = 20
Si tomamos currentRightPosition = 15, su currentLeftPosition es 7. El caso 1 se aplica aquí y entonces L[15] = 3. i-palíndromo izquierdo en la posición 7 es «bab», que está completamente contenido en el centro del palíndromo en la posición 11 (que es «dbabcbabd»). Podemos ver que el palíndromo i-derecho (en la posición 15) no puede expandirse más que el palíndromo i-izquierdo (en la posición 7).

Si hubiera una posibilidad de expansión, i-left palindrome ya podría haberse expandido más. Pero no existe tal posibilidad ya que el palíndromo i-izquierdo es el prefijo del palíndromo central. Entonces, debido a la propiedad de simetría, el palíndromo i-derecho será exactamente igual que el palíndromo i-izquierdo y no puede expandirse más. Esto hace que L[posiciónDerechaActual] = L[posiciónIzquierdaActual] en el Caso 1.

Ahora, si consideramos la posición central = 19, entonces la posición izquierda central = 12 y la posición derecha central = 26.
Si tomamos la posición derecha actual = 23, la posición izquierda actual es 15. Aquí se aplica el caso 2, por lo que L[23] = 3. i-palíndromo izquierdo en la posición 15 es “ bab” que está completamente contenido en el palíndromo central en la posición 19 (que es “babdbab”). En el Caso 2, donde el palíndromo i-izquierdo es el prefijo del palíndromo central, el palíndromo i-derecho no puede expandirse más que la longitud del palíndromo i-izquierdo porque el palíndromo central es el sufijo de la string de entrada, por lo que no quedan más caracteres para comparar y expandir . Esto hace que L[posiciónDerechaActual] = L[posiciónIzquierdaActual] en el Caso 2.

Caso 1: L[posiciónDerechaActual] = L[posiciónIzquierdaActual] se aplica cuando:

• i-el palíndromo izquierdo está completamente contenido en el palíndromo central
• i-palíndromo izquierdo NO es un prefijo del palíndromo central

Las dos condiciones anteriores se cumplen cuando
L[posición izquierda actual] < posición derecha central – posición derecha actual

Caso 2: L[posiciónDerechaActual] = L[posiciónIzquierdaActual] se aplica cuando:

• i-palíndromo izquierdo es prefijo del palíndromo central (también significa completamente contenido)
• el palíndromo central es el sufijo de la string de entrada

Las condiciones anteriores se cumplen cuando
L[posición izquierda actual] = posición derecha central – posición derecha actual (para la ^primera condición) Y
posición derecha central = 2*N donde N es la longitud de la string de entrada N (para la ^segunda condición).

Caso 3: L[posiciónDerechaActual] > = L[posiciónIzquierdaActual] se aplica cuando:

• i-palíndromo izquierdo es prefijo del palíndromo central (y por lo tanto i-palíndromo izquierdo está completamente contenido en el palíndromo central)
• el palíndromo central NO es el sufijo de la string de entrada

Las condiciones anteriores se cumplen cuando
L[posición izquierda actual] = posición derecha central – posición derecha actual (para la ^primera condición) Y
posición derecha central < 2*N donde N es la longitud de la string de entrada N (para la ^segunda condición).
En este caso, existe la posibilidad de una expansión del i-palíndromo derecho y, por lo tanto, la longitud del i-palíndromo derecho es al menos tan larga como la longitud del i-palíndromo izquierdo.

Caso 4: L[posiciónDerechaActual] > = posiciónDerechaCentro – PosiciónDerechaActual se aplica cuando:

• i-el palíndromo izquierdo NO está completamente contenido en el palíndromo central

La condición anterior se cumple cuando
L[posición izquierda actual] > posición derecha central – posición derecha actual.
En este caso, la longitud del palíndromo derecho i es al menos igual (posición derecha central – posición derecha actual) y existe la posibilidad de expansión del palíndromo derecho i.

En la siguiente figura,

                          (click to see it clearly)
                    

Si tomamos la posición central 7, entonces el caso 3 se aplica en la posición derecha actual 11 porque el palíndromo i-izquierdo en la posición izquierda actual 3 es un prefijo del palíndromo central y el palíndromo i-derecho no es un sufijo de la string de entrada, por lo que aquí L[11] = 9, que es mayor que i-longitud del palíndromo izquierdo L[3] = 3. En el caso, se garantiza que L[11] será al menos 3, por lo que en la implementación, primero ^establecemos L[11] = 3 y luego tratamos de expandirlo comparando los caracteres en el lado izquierdo y derecho a partir de la distancia 4 (hasta la distancia 3, ya se sabe que los caracteres coincidirán).

Si tomamos la posición central 11, entonces el caso 4 se aplica en la posición derecha actual 15 porque L[posición izquierda actual] = L [7] = 7 > posición derecha central – posición derecha actual = 20 – 15 = 5. En el caso, se garantiza que L[15] ser al menos 5, y así en la implementación, primero ^establecemos L[15] = 5 y luego tratamos de expandirlo comparando los caracteres en el lado izquierdo y derecho comenzando desde la distancia 5 (hasta la distancia 5, ya está sabe que los caracteres coincidirán).

Ahora, un punto que queda por discutir es, cuando trabajamos en una posición central y calculamos longitudes LPS para diferentes posiciones derechas, cómo saber cuál sería la siguiente posición central. Cambiamos centerPosition a currentRightPosition si el palíndromo centrado en currentRightPosition se expande más allá de centerRightPosition.

Aquí hemos visto cuatro casos diferentes sobre cómo la longitud de LPS de una posición dependerá de la longitud de LPS de una posición anterior.
En la Parte 3 , hemos discutido la implementación del código y también hemos visto estos cuatro casos de una manera diferente e implementamos eso también.

Este artículo es una contribución de Anurag Singh . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.