En Algoritmo de Manacher Parte 1 y Parte 2 , repasamos algunos de los conceptos básicos, entendimos la array de longitud LPS y cómo calcularla de manera eficiente en base a cuatro casos. En la Parte 3 , implementamos lo mismo.
Aquí revisaremos los cuatro casos nuevamente y trataremos de verlo de manera diferente e implementar lo mismo.
Los cuatro casos dependen del valor de longitud LPS en la posición izquierda actual (L[iMirror]) y el valor de (posición derecha central – posición derecha actual), es decir (R – i). Estas dos informaciones se conocen de antemano, lo que nos ayuda a reutilizar la información anterior disponible y evitar comparaciones de caracteres innecesarias.
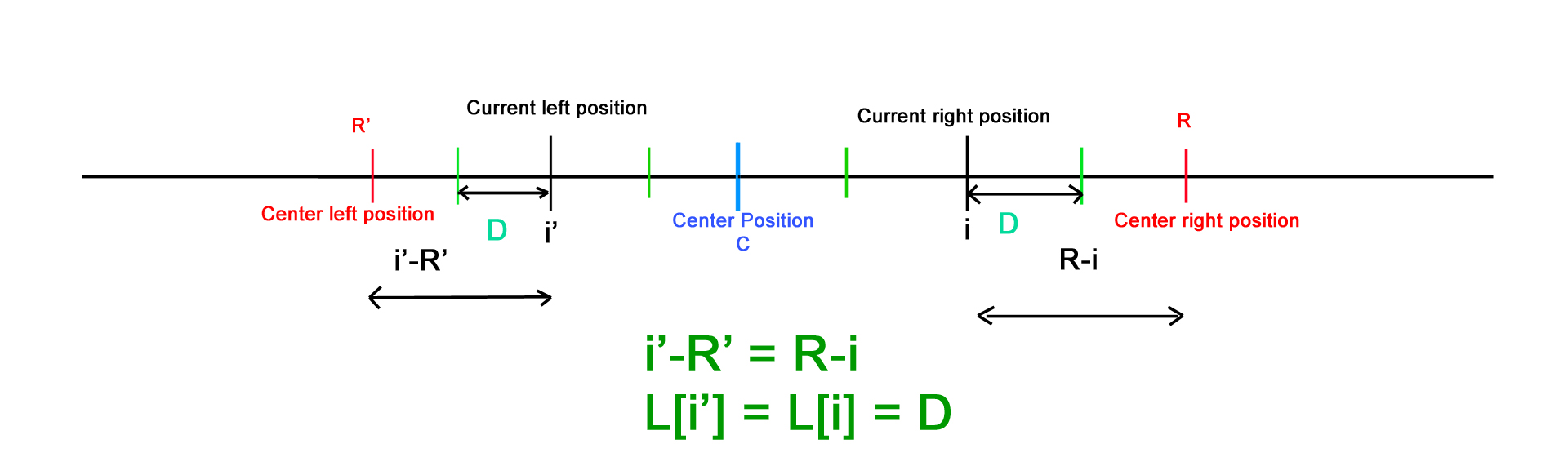
Si observamos los cuatro casos, veremos que primero establecemos un mínimo de L[iMirror] y Ri a L[i] y luego tratamos de expandir el palíndromo en cualquier caso que pueda expandirse.
La observación anterior puede parecer más intuitiva, más fácil de entender e implementar, dado que uno comprende la array de longitud LPS, la posición, el índice, la propiedad de simetría, etc.
Implementación:
C++
// A C program to implement Manacher’s Algorithm
#include <stdio.h>
#include <string.h>
char text[100];
int min(int a, int b)
{
int res = a;
if(b < a)
res = b;
return res;
}
void findLongestPalindromicString()
{
int N = strlen(text);
if(N == 0)
return;
N = 2*N + 1; //Position count
int L[N]; //LPS Length Array
L[0] = 0;
L[1] = 1;
int C = 1; //centerPosition
int R = 2; //centerRightPosition
int i = 0; //currentRightPosition
int iMirror; //currentLeftPosition
int maxLPSLength = 0;
int maxLPSCenterPosition = 0;
int start = -1;
int end = -1;
int diff = -1;
//Uncomment it to print LPS Length array
//printf("%d %d ", L[0], L[1]);
for (i = 2; i < N; i++)
{
//get currentLeftPosition iMirror for currentRightPosition i
iMirror = 2*C-i;
L[i] = 0;
diff = R - i;
//If currentRightPosition i is within centerRightPosition R
if(diff > 0)
L[i] = min(L[iMirror], diff);
//Attempt to expand palindrome centered at currentRightPosition i
//Here for odd positions, we compare characters and
//if match then increment LPS Length by ONE
//If even position, we just increment LPS by ONE without
//any character comparison
while ( ((i + L[i]) < N && (i - L[i]) > 0) &&
( ((i + L[i] + 1) % 2 == 0) ||
(text[(i + L[i] + 1)/2] == text[(i - L[i] - 1)/2] )))
{
L[i]++;
}
if(L[i] > maxLPSLength) // Track maxLPSLength
{
maxLPSLength = L[i];
maxLPSCenterPosition = i;
}
//If palindrome centered at currentRightPosition i
//expand beyond centerRightPosition R,
//adjust centerPosition C based on expanded palindrome.
if (i + L[i] > R)
{
C = i;
R = i + L[i];
}
//Uncomment it to print LPS Length array
//printf("%d ", L[i]);
}
//printf("\n");
start = (maxLPSCenterPosition - maxLPSLength)/2;
end = start + maxLPSLength - 1;
printf("LPS of string is %s : ", text);
for(i=start; i<=end; i++)
printf("%c", text[i]);
printf("\n");
}
int main(int argc, char *argv[])
{
strcpy(text, "babcbabcbaccba");
findLongestPalindromicString();
strcpy(text, "abaaba");
findLongestPalindromicString();
strcpy(text, "abababa");
findLongestPalindromicString();
strcpy(text, "abcbabcbabcba");
findLongestPalindromicString();
strcpy(text, "forgeeksskeegfor");
findLongestPalindromicString();
strcpy(text, "caba");
findLongestPalindromicString();
strcpy(text, "abacdfgdcaba");
findLongestPalindromicString();
strcpy(text, "abacdfgdcabba");
findLongestPalindromicString();
strcpy(text, "abacdedcaba");
findLongestPalindromicString();
return 0;
}
Java
// Java program to implement Manacher's Algorithm
import java.util.*;
class GFG
{
static void findLongestPalindromicString(String text)
{
int N = text.length();
if (N == 0)
return;
N = 2 * N + 1; // Position count
int[] L = new int[N + 1]; // LPS Length Array
L[0] = 0;
L[1] = 1;
int C = 1; // centerPosition
int R = 2; // centerRightPosition
int i = 0; // currentRightPosition
int iMirror; // currentLeftPosition
int maxLPSLength = 0;
int maxLPSCenterPosition = 0;
int start = -1;
int end = -1;
int diff = -1;
// Uncomment it to print LPS Length array
// printf("%d %d ", L[0], L[1]);
for (i = 2; i < N; i++)
{
// get currentLeftPosition iMirror
// for currentRightPosition i
iMirror = 2 * C - i;
L[i] = 0;
diff = R - i;
// If currentRightPosition i is within
// centerRightPosition R
if (diff > 0)
L[i] = Math.min(L[iMirror], diff);
// Attempt to expand palindrome centered at
// currentRightPosition i. Here for odd positions,
// we compare characters and if match then
// increment LPS Length by ONE. If even position,
// we just increment LPS by ONE without
// any character comparison
while (((i + L[i]) + 1 < N && (i - L[i]) > 0) &&
(((i + L[i] + 1) % 2 == 0) ||
(text.charAt((i + L[i] + 1) / 2) ==
text.charAt((i - L[i] - 1) / 2))))
{
L[i]++;
}
if (L[i] > maxLPSLength) // Track maxLPSLength
{
maxLPSLength = L[i];
maxLPSCenterPosition = i;
}
// If palindrome centered at currentRightPosition i
// expand beyond centerRightPosition R,
// adjust centerPosition C based on expanded palindrome.
if (i + L[i] > R)
{
C = i;
R = i + L[i];
}
// Uncomment it to print LPS Length array
// printf("%d ", L[i]);
}
start = (maxLPSCenterPosition - maxLPSLength) / 2;
end = start + maxLPSLength - 1;
System.out.printf("LPS of string is %s : ", text);
for (i = start; i <= end; i++)
System.out.print(text.charAt(i));
System.out.println();
}
// Driver Code
public static void main(String[] args)
{
String text = "babcbabcbaccba";
findLongestPalindromicString(text);
text = "abaaba";
findLongestPalindromicString(text);
text = "abababa";
findLongestPalindromicString(text);
text = "abcbabcbabcba";
findLongestPalindromicString(text);
text = "forgeeksskeegfor";
findLongestPalindromicString(text);
text = "caba";
findLongestPalindromicString(text);
text = "abacdfgdcaba";
findLongestPalindromicString(text);
text = "abacdfgdcabba";
findLongestPalindromicString(text);
text = "abacdedcaba";
findLongestPalindromicString(text);
}
}
// This code is contributed by
// sanjeev2552
Python3
# Python program to implement Manacher's Algorithm
def findLongestPalindromicString(text):
N = len(text)
if N == 0:
return
N = 2*N+1 # Position count
L = [0] * N
L[0] = 0
L[1] = 1
C = 1 # centerPosition
R = 2 # centerRightPosition
i = 0 # currentRightPosition
iMirror = 0 # currentLeftPosition
maxLPSLength = 0
maxLPSCenterPosition = 0
start = -1
end = -1
diff = -1
# Uncomment it to print LPS Length array
# printf("%d %d ", L[0], L[1]);
for i in range(2,N):
# get currentLeftPosition iMirror for currentRightPosition i
iMirror = 2*C-i
L[i] = 0
diff = R - i
# If currentRightPosition i is within centerRightPosition R
if diff > 0:
L[i] = min(L[iMirror], diff)
# Attempt to expand palindrome centered at currentRightPosition i
# Here for odd positions, we compare characters and
# if match then increment LPS Length by ONE
# If even position, we just increment LPS by ONE without
# any character comparison
try:
while ((i + L[i]) < N and (i - L[i]) > 0) and \
(((i + L[i] + 1) % 2 == 0) or \
(text[(i + L[i] + 1) // 2] == text[(i - L[i] - 1) // 2])):
L[i]+=1
except Exception as e:
pass
if L[i] > maxLPSLength: # Track maxLPSLength
maxLPSLength = L[i]
maxLPSCenterPosition = i
# If palindrome centered at currentRightPosition i
# expand beyond centerRightPosition R,
# adjust centerPosition C based on expanded palindrome.
if i + L[i] > R:
C = i
R = i + L[i]
# Uncomment it to print LPS Length array
# printf("%d ", L[i]);
start = (maxLPSCenterPosition - maxLPSLength) // 2
end = start + maxLPSLength - 1
print ("LPS of string is " + text + " : ",text[start:end+1])
# Driver program
text1 = "babcbabcbaccba"
findLongestPalindromicString(text1)
text2 = "abaaba"
findLongestPalindromicString(text2)
text3 = "abababa"
findLongestPalindromicString(text3)
text4 = "abcbabcbabcba"
findLongestPalindromicString(text4)
text5 = "forgeeksskeegfor"
findLongestPalindromicString(text5)
text6 = "caba"
findLongestPalindromicString(text6)
text7 = "abacdfgdcaba"
findLongestPalindromicString(text7)
text8 = "abacdfgdcabba"
findLongestPalindromicString(text8)
text9 = "abacdedcaba"
findLongestPalindromicString(text9)
# This code is contributed by BHAVYA JAIN
C#
// C# program to implement Manacher's Algorithm
using System;
class GFG
{
static void findLongestPalindromicString(String text)
{
int N = text.Length;
if (N == 0)
return;
N = 2 * N + 1; // Position count
int[] L = new int[N + 1]; // LPS Length Array
L[0] = 0;
L[1] = 1;
int C = 1; // centerPosition
int R = 2; // centerRightPosition
int i = 0; // currentRightPosition
int iMirror; // currentLeftPosition
int maxLPSLength = 0;
int maxLPSCenterPosition = 0;
int start = -1;
int end = -1;
int diff = -1;
// Uncomment it to print LPS Length array
// printf("%d %d ", L[0], L[1]);
for (i = 2; i < N; i++)
{
// get currentLeftPosition iMirror
// for currentRightPosition i
iMirror = 2 * C - i;
L[i] = 0;
diff = R - i;
// If currentRightPosition i is within
// centerRightPosition R
if (diff > 0)
L[i] = Math.Min(L[iMirror], diff);
// Attempt to expand palindrome centered at
// currentRightPosition i. Here for odd positions,
// we compare characters and if match then
// increment LPS Length by ONE. If even position,
// we just increment LPS by ONE without
// any character comparison
while (((i + L[i]) + 1 < N && (i - L[i]) > 0) &&
(((i + L[i] + 1) % 2 == 0) ||
(text[(i + L[i] + 1) / 2] ==
text[(i - L[i] - 1) / 2])))
{
L[i]++;
}
if (L[i] > maxLPSLength) // Track maxLPSLength
{
maxLPSLength = L[i];
maxLPSCenterPosition = i;
}
// If palindrome centered at currentRightPosition i
// expand beyond centerRightPosition R,
// adjust centerPosition C based on expanded palindrome.
if (i + L[i] > R)
{
C = i;
R = i + L[i];
}
// Uncomment it to print LPS Length array
// printf("%d ", L[i]);
}
start = (maxLPSCenterPosition - maxLPSLength) / 2;
end = start + maxLPSLength - 1;
Console.Write("LPS of string is {0} : ", text);
for (i = start; i <= end; i++)
Console.Write(text[i]);
Console.WriteLine();
}
// Driver Code
public static void Main(String[] args)
{
String text = "babcbabcbaccba";
findLongestPalindromicString(text);
text = "abaaba";
findLongestPalindromicString(text);
text = "abababa";
findLongestPalindromicString(text);
text = "abcbabcbabcba";
findLongestPalindromicString(text);
text = "forgeeksskeegfor";
findLongestPalindromicString(text);
text = "caba";
findLongestPalindromicString(text);
text = "abacdfgdcaba";
findLongestPalindromicString(text);
text = "abacdfgdcabba";
findLongestPalindromicString(text);
text = "abacdedcaba";
findLongestPalindromicString(text);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript program to implement Manacher's Algorithm
function findLongestPalindromicString(text)
{
let N = text.length;
if (N == 0)
return;
N = 2 * N + 1; // Position count
let L = new Array(N + 1); // LPS Length Array
L[0] = 0;
L[1] = 1;
let C = 1; // centerPosition
let R = 2; // centerRightPosition
let i = 0; // currentRightPosition
let iMirror; // currentLeftPosition
let maxLPSLength = 0;
let maxLPSCenterPosition = 0;
let start = -1;
let end = -1;
let diff = -1;
// Uncomment it to print LPS Length array
// printf("%d %d ", L[0], L[1]);
for (i = 2; i < N; i++)
{
// get currentLeftPosition iMirror
// for currentRightPosition i
iMirror = 2 * C - i;
L[i] = 0;
diff = R - i;
// If currentRightPosition i is within
// centerRightPosition R
if (diff > 0)
L[i] = Math.min(L[iMirror], diff);
// Attempt to expand palindrome centered at
// currentRightPosition i. Here for odd positions,
// we compare characters and if match then
// increment LPS Length by ONE. If even position,
// we just increment LPS by ONE without
// any character comparison
while (((i + L[i]) + 1 < N && (i - L[i]) > 0) &&
(((i + L[i] + 1) % 2 == 0) ||
(text[Math.floor((i + L[i] + 1) / 2)] ==
text[Math.floor((i - L[i] - 1) / 2)])))
{
L[i]++;
}
if (L[i] > maxLPSLength) // Track maxLPSLength
{
maxLPSLength = L[i];
maxLPSCenterPosition = i;
}
// If palindrome centered at currentRightPosition i
// expand beyond centerRightPosition R,
// adjust centerPosition C based on expanded palindrome.
if (i + L[i] > R)
{
C = i;
R = i + L[i];
}
// Uncomment it to print LPS Length array
// printf("%d ", L[i]);
}
start = (maxLPSCenterPosition - maxLPSLength) / 2;
end = start + maxLPSLength - 1;
document.write("LPS of string is "+text+" : ");
for (i = start; i <= end; i++)
document.write(text[i]);
document.write("<br>");
}
// Driver Code
let text = "babcbabcbaccba";
findLongestPalindromicString(text);
text = "abaaba";
findLongestPalindromicString(text);
text = "abababa";
findLongestPalindromicString(text);
text = "abcbabcbabcba";
findLongestPalindromicString(text);
text = "forgeeksskeegfor";
findLongestPalindromicString(text);
text = "caba";
findLongestPalindromicString(text);
text = "abacdfgdcaba";
findLongestPalindromicString(text);
text = "abacdfgdcabba";
findLongestPalindromicString(text);
text = "abacdedcaba";
findLongestPalindromicString(text);
// This code is contributed by unknown2108
</script>
LPS of string is babcbabcbaccba : abcbabcba LPS of string is abaaba : abaaba LPS of string is abababa : abababa LPS of string is abcbabcbabcba : abcbabcbabcba LPS of string is forgeeksskeegfor : geeksskeeg LPS of string is caba : aba LPS of string is abacdfgdcaba : aba LPS of string is abacdfgdcabba : abba LPS of string is abacdedcaba : abacdedcaba
Complejidad temporal: O(n)
Espacio auxiliar: O(n)
Otros enfoques:
Hemos discutido dos enfoques aquí. Uno en la Parte 3 y otro en el artículo actual. En ambos enfoques, trabajamos en una string dada. Aquí tuvimos que manejar las posiciones pares e impares de manera diferente al comparar los caracteres para la expansión (porque las posiciones pares no representan ningún carácter en la string).
Para evitar este manejo diferente de las posiciones pares e impares, necesitamos hacer que las posiciones pares también representen algún carácter (en realidad, todas las posiciones pares deberían representar el MISMO carácter porque DEBEN coincidir durante la comparación de caracteres). Una forma de hacer esto es establecer algún carácter en todas las posiciones pares modificando la string dada o creando una nueva copia de la string dada. Por ejemplo, si la string de entrada es «abcb», la nueva string debe ser «#a#b#c#b#» si agregamos # como carácter único en las posiciones pares.
Los dos enfoques discutidos ya se pueden modificar un poco para que funcionen en una string modificada donde no se necesitará un manejo diferente de las posiciones pares e impares.
También podemos agregar dos caracteres DIFERENTES (que aún no se usan en ninguna parte de la string en posiciones pares e impares) al principio y al final de la string como centinelas para evitar la verificación de límites. Con estos cambios, la string «abcb» se verá como «^#a#b#c#b#$», donde ^ y $son centinelas.
Esta implementación puede parecer más limpia con el costo de más memoria.
No los estamos implementando aquí, ya que es un cambio simple en implementaciones dadas.
La implementación del enfoque discutido en el artículo actual sobre una string modificada se puede encontrar en la substring palindrómica más larga, parte II y una traducción de Java de la misma por parte de Princeton.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA