Problema: Se coloca un caballo en el primer bloque de un tablero vacío y, moviéndose según las reglas del ajedrez, debe visitar cada casilla exactamente una vez.
A continuación se muestra un ejemplo de la ruta seguida por Knight para cubrir todas las celdas. La siguiente cuadrícula representa un tablero de ajedrez con 8 x 8 celdas. Los números en las celdas indican el número de movimiento del Caballo.
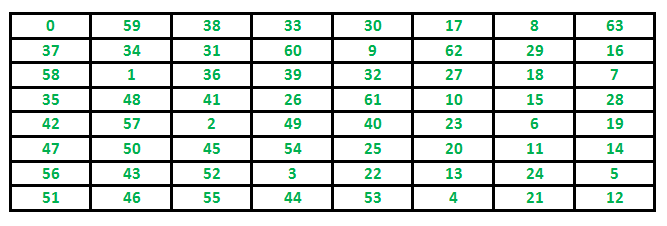
Hemos discutido el algoritmo de retroceso para la solución del recorrido de Knight . En este post se discute la heurística de Warnsdorff .
Regla de Warnsdorff:
- Podemos partir de cualquier posición inicial del caballo en el tablero.
- Siempre nos movemos a una casilla adyacente no visitada con un grado mínimo (número mínimo de adyacentes no visitados).
Este algoritmo también puede aplicarse de manera más general a cualquier gráfico.
Algunas definiciones:
- Se puede acceder a una posición Q desde una posición P si P puede moverse a Q con un solo movimiento de caballo y Q aún no ha sido visitada.
- La accesibilidad de una posición P es el número de posiciones accesibles desde P.
Algoritmo:
- Establecer P para que sea una posición inicial aleatoria en el tablero
- Marque el tablero en P con el número de movimiento «1»
- Haz lo siguiente para cada número de movimiento del 2 al número de casillas en el tablero:
- Sea S el conjunto de posiciones accesibles desde P.
- Establezca P para que sea la posición en S con accesibilidad mínima
- Marque el tablero en P con el número de movimiento actual
- Devuelva el tablero marcado: cada casilla se marcará con el número de movimiento en el que se visita.
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ program to for Knight's tour problem using
// Warnsdorff's algorithm
#include <bits/stdc++.h>
#define N 8
// Move pattern on basis of the change of
// x coordinates and y coordinates respectively
static int cx[N] = {1,1,2,2,-1,-1,-2,-2};
static int cy[N] = {2,-2,1,-1,2,-2,1,-1};
// function restricts the knight to remain within
// the 8x8 chessboard
bool limits(int x, int y)
{
return ((x >= 0 && y >= 0) && (x < N && y < N));
}
/* Checks whether a square is valid and empty or not */
bool isempty(int a[], int x, int y)
{
return (limits(x, y)) && (a[y*N+x] < 0);
}
/* Returns the number of empty squares adjacent
to (x, y) */
int getDegree(int a[], int x, int y)
{
int count = 0;
for (int i = 0; i < N; ++i)
if (isempty(a, (x + cx[i]), (y + cy[i])))
count++;
return count;
}
// Picks next point using Warnsdorff's heuristic.
// Returns false if it is not possible to pick
// next point.
bool nextMove(int a[], int *x, int *y)
{
int min_deg_idx = -1, c, min_deg = (N+1), nx, ny;
// Try all N adjacent of (*x, *y) starting
// from a random adjacent. Find the adjacent
// with minimum degree.
int start = rand()%N;
for (int count = 0; count < N; ++count)
{
int i = (start + count)%N;
nx = *x + cx[i];
ny = *y + cy[i];
if ((isempty(a, nx, ny)) &&
(c = getDegree(a, nx, ny)) < min_deg)
{
min_deg_idx = i;
min_deg = c;
}
}
// IF we could not find a next cell
if (min_deg_idx == -1)
return false;
// Store coordinates of next point
nx = *x + cx[min_deg_idx];
ny = *y + cy[min_deg_idx];
// Mark next move
a[ny*N + nx] = a[(*y)*N + (*x)]+1;
// Update next point
*x = nx;
*y = ny;
return true;
}
/* displays the chessboard with all the
legal knight's moves */
void print(int a[])
{
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
printf("%d\t",a[j*N+i]);
printf("\n");
}
}
/* checks its neighbouring squares */
/* If the knight ends on a square that is one
knight's move from the beginning square,
then tour is closed */
bool neighbour(int x, int y, int xx, int yy)
{
for (int i = 0; i < N; ++i)
if (((x+cx[i]) == xx)&&((y + cy[i]) == yy))
return true;
return false;
}
/* Generates the legal moves using warnsdorff's
heuristics. Returns false if not possible */
bool findClosedTour()
{
// Filling up the chessboard matrix with -1's
int a[N*N];
for (int i = 0; i< N*N; ++i)
a[i] = -1;
// Random initial position
int sx = rand()%N;
int sy = rand()%N;
// Current points are same as initial points
int x = sx, y = sy;
a[y*N+x] = 1; // Mark first move.
// Keep picking next points using
// Warnsdorff's heuristic
for (int i = 0; i < N*N-1; ++i)
if (nextMove(a, &x, &y) == 0)
return false;
// Check if tour is closed (Can end
// at starting point)
if (!neighbour(x, y, sx, sy))
return false;
print(a);
return true;
}
// Driver code
int main()
{
// To make sure that different random
// initial positions are picked.
srand(time(NULL));
// While we don't get a solution
while (!findClosedTour())
{
;
}
return 0;
}
Java
// Java program to for Knight's tour problem using
// Warnsdorff's algorithm
import java.util.concurrent.ThreadLocalRandom;
class GFG
{
public static final int N = 8;
// Move pattern on basis of the change of
// x coordinates and y coordinates respectively
public static final int cx[] = {1, 1, 2, 2, -1, -1, -2, -2};
public static final int cy[] = {2, -2, 1, -1, 2, -2, 1, -1};
// function restricts the knight to remain within
// the 8x8 chessboard
boolean limits(int x, int y)
{
return ((x >= 0 && y >= 0) &&
(x < N && y < N));
}
/* Checks whether a square is valid and
empty or not */
boolean isempty(int a[], int x, int y)
{
return (limits(x, y)) && (a[y * N + x] < 0);
}
/* Returns the number of empty squares
adjacent to (x, y) */
int getDegree(int a[], int x, int y)
{
int count = 0;
for (int i = 0; i < N; ++i)
if (isempty(a, (x + cx[i]),
(y + cy[i])))
count++;
return count;
}
// Picks next point using Warnsdorff's heuristic.
// Returns false if it is not possible to pick
// next point.
Cell nextMove(int a[], Cell cell)
{
int min_deg_idx = -1, c,
min_deg = (N + 1), nx, ny;
// Try all N adjacent of (*x, *y) starting
// from a random adjacent. Find the adjacent
// with minimum degree.
int start = ThreadLocalRandom.current().nextInt(1000) % N;
for (int count = 0; count < N; ++count)
{
int i = (start + count) % N;
nx = cell.x + cx[i];
ny = cell.y + cy[i];
if ((isempty(a, nx, ny)) &&
(c = getDegree(a, nx, ny)) < min_deg)
{
min_deg_idx = i;
min_deg = c;
}
}
// IF we could not find a next cell
if (min_deg_idx == -1)
return null;
// Store coordinates of next point
nx = cell.x + cx[min_deg_idx];
ny = cell.y + cy[min_deg_idx];
// Mark next move
a[ny * N + nx] = a[(cell.y) * N +
(cell.x)] + 1;
// Update next point
cell.x = nx;
cell.y = ny;
return cell;
}
/* displays the chessboard with all the
legal knight's moves */
void print(int a[])
{
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
System.out.printf("%d\t", a[j * N + i]);
System.out.printf("\n");
}
}
/* checks its neighbouring squares */
/* If the knight ends on a square that is one
knight's move from the beginning square,
then tour is closed */
boolean neighbour(int x, int y, int xx, int yy)
{
for (int i = 0; i < N; ++i)
if (((x + cx[i]) == xx) &&
((y + cy[i]) == yy))
return true;
return false;
}
/* Generates the legal moves using warnsdorff's
heuristics. Returns false if not possible */
boolean findClosedTour()
{
// Filling up the chessboard matrix with -1's
int a[] = new int[N * N];
for (int i = 0; i < N * N; ++i)
a[i] = -1;
// initial position
int sx = 3;
int sy = 2;
// Current points are same as initial points
Cell cell = new Cell(sx, sy);
a[cell.y * N + cell.x] = 1; // Mark first move.
// Keep picking next points using
// Warnsdorff's heuristic
Cell ret = null;
for (int i = 0; i < N * N - 1; ++i)
{
ret = nextMove(a, cell);
if (ret == null)
return false;
}
// Check if tour is closed (Can end
// at starting point)
if (!neighbour(ret.x, ret.y, sx, sy))
return false;
print(a);
return true;
}
// Driver Code
public static void main(String[] args)
{
// While we don't get a solution
while (!new GFG().findClosedTour())
{
;
}
}
}
class Cell
{
int x;
int y;
public Cell(int x, int y)
{
this.x = x;
this.y = y;
}
}
// This code is contributed by SaeedZarinfam
C#
//C# program for Knight’s tour
//problem using Warnsdorff’salgorithm
using System;
using System.Collections;
using System.Collections.Generic;
public class GFG{
public static int N = 8;
// Move pattern on basis of the change of
// x coordinates and y coordinates respectively
public int[] cx = new int[] {1, 1, 2, 2, -1, -1, -2, -2};
public int[] cy = new int[] {2, -2, 1, -1, 2, -2, 1, -1};
// function restricts the knight to remain within
// the 8x8 chessboard
bool limits(int x, int y)
{
return ((x >= 0 && y >= 0) && (x < N && y < N));
}
/* Checks whether a square is valid and
empty or not */
bool isempty(int[] a, int x, int y)
{
return ((limits(x, y)) && (a[y * N + x] < 0));
}
/* Returns the number of empty squares
adjacent to (x, y) */
int getDegree(int[] a, int x, int y)
{
int count = 0;
for (int i = 0; i < N; ++i)
if (isempty(a, (x + cx[i]),
(y + cy[i])))
count++;
return count;
}
// Picks next point using Warnsdorff's heuristic.
// Returns false if it is not possible to pick
// next point.
Cell nextMove(int[] a, Cell cell)
{
int min_deg_idx = -1, c,
min_deg = (N + 1), nx, ny;
// Try all N adjacent of (*x, *y) starting
// from a random adjacent. Find the adjacent
// with minimum degree.
Random random = new Random();
int start=random.Next(0, 1000);
for (int count = 0; count < N; ++count)
{
int i = (start + count) % N;
nx = cell.x + cx[i];
ny = cell.y + cy[i];
if ((isempty(a, nx, ny)) &&
(c = getDegree(a, nx, ny)) < min_deg)
{
min_deg_idx = i;
min_deg = c;
}
}
// IF we could not find a next cell
if (min_deg_idx == -1)
return null;
// Store coordinates of next point
nx = cell.x + cx[min_deg_idx];
ny = cell.y + cy[min_deg_idx];
// Mark next move
a[ny * N + nx] = a[(cell.y) * N +
(cell.x)] + 1;
// Update next point
cell.x = nx;
cell.y = ny;
return cell;
}
/* displays the chessboard with all the
legal knight's moves */
void print(int[] a)
{
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
Console.Write(a[j * N + i]+"\t");
Console.Write("\n");
}
}
/* checks its neighbouring squares */
/* If the knight ends on a square that is one
knight's move from the beginning square,
then tour is closed */
bool neighbour(int x, int y, int xx, int yy)
{
for (int i = 0; i < N; ++i)
if (((x + cx[i]) == xx) &&
((y + cy[i]) == yy))
return true;
return false;
}
/* Generates the legal moves using warnsdorff's
heuristics. Returns false if not possible */
bool findClosedTour()
{
// Filling up the chessboard matrix with -1's
int[] a = new int[N * N];
for (int i = 0; i < N * N; ++i)
a[i] = -1;
// initial position
int sx = 3;
int sy = 2;
// Current points are same as initial points
Cell cell = new Cell(sx, sy);
a[cell.y * N + cell.x] = 1; // Mark first move.
// Keep picking next points using
// Warnsdorff's heuristic
Cell ret = null;
for (int i = 0; i < N * N - 1; ++i)
{
ret = nextMove(a, cell);
if (ret == null)
return false;
}
// Check if tour is closed (Can end
// at starting point)
if (!neighbour(ret.x, ret.y, sx, sy))
return false;
print(a);
return true;
}
static public void Main (){
// While we don't get a solution
while (!new GFG().findClosedTour())
{
;
}
}
}
class Cell
{
public int x;
public int y;
public Cell(int x, int y)
{
this.x = x;
this.y = y;
}
}
//This code is contributed by shruti456rawal
Producción:
59 14 63 32 1 16 19 34 62 31 60 15 56 33 2 17 13 58 55 64 49 18 35 20 30 61 42 57 54 51 40 3 43 12 53 50 41 48 21 36 26 29 44 47 52 39 4 7 11 46 27 24 9 6 37 22 28 25 10 45 38 23 8 5
El problema del camino hamiltoniano es NP-difícil en general. En la práctica, la heurística de Warnsdorff encuentra con éxito una solución en tiempo lineal.
¿Lo sabías?
“En un tablero de 8 × 8, hay exactamente 26 534 728 821 064 recorridos cerrados dirigidos (es decir, dos recorridos a lo largo del mismo camino que viajan en direcciones opuestas se cuentan por separado, al igual que las rotaciones y los reflejos). ¡La cantidad de recorridos cerrados no dirigidos es la mitad de este número, ya que cada recorrido se puede rastrear al revés!
Este artículo es una contribución de Uddalak Bhaduri . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA