Una coincidencia en un gráfico bipartito es un conjunto de aristas elegidas de tal manera que no hay dos aristas que compartan un punto final. Una coincidencia máxima es una coincidencia de tamaño máximo (número máximo de aristas). En un emparejamiento máximo, si se le añade alguna arista, deja de ser un emparejamiento. Puede haber más de una coincidencia máxima para un gráfico bipartito dado.
Hemos discutido la importancia de la coincidencia máxima y el enfoque basado en Ford Fulkerson para la coincidencia bipartita máxima en una publicación anterior . La complejidad temporal del algoritmo basado en Ford Fulkerson es O(V x E). El algoritmo de Hopcroft Karp es una mejora que se ejecuta en tiempo O(√V x E). Definamos algunos términos antes de discutir el algoritmo.
Node Libre o Vértice: Dada una M coincidente, un Node que no forma parte de la coincidencia se llama Node libre. Inicialmente, todos los vértices están libres (consulte el primer gráfico del diagrama a continuación). En el segundo gráfico, u2 y v2 están libres. En el tercer grafo, ningún vértice está libre.
Aristas coincidentes y no coincidentes: dada una M coincidente, las aristas que forman parte de la coincidencia se denominan aristas coincidentes y las aristas que no forman parte de M (o conectan Nodes libres) se denominan aristas no coincidentes. En el primer gráfico, todos los bordes no coinciden. En el segundo gráfico, (u0, v1), (u1, v0) y (u3, v3) coinciden y otros no coinciden.
Caminos alternos: Dada una M coincidente, un camino alternativo es un camino en el que los bordes pertenecen alternativamente a los coincidentes y no coincidentes. Todos los caminos de un solo borde son caminos alternos. Ejemplos de rutas alternas en el gráfico central son u0-v1-u2 y u2-v1-u0-v2.
Camino de aumento : dada una M coincidente, un camino de aumento es un camino alterno que comienza y termina en vértices libres. Todos los caminos de un solo borde que comienzan y terminan con vértices libres son caminos de aumento. En el siguiente diagrama, las rutas de aumento se resaltan en color azul. Tenga en cuenta que la ruta de aumento siempre tiene un borde coincidente adicional. El algoritmo Hopcroft Karp se basa en el siguiente concepto. Una M coincidente no es máxima si existe una ruta de aumento. También es cierto de otra manera, es decir, una coincidencia es máxima si no existe una ruta de aumento . Por lo tanto, la idea es buscar rutas de aumento una por una. Y agregue las rutas encontradas a la coincidencia actual.
Algoritmo Hopcroft Karp:
- Inicialice Maximal Matching M como vacío.
- Mientras exista un Camino de Aumento p
- Elimine los bordes coincidentes de p de M y agregue los bordes no coincidentes de p a M
- (Esto aumenta el tamaño de M en 1 ya que p comienza y termina con un vértice libre)
- Vuelve m
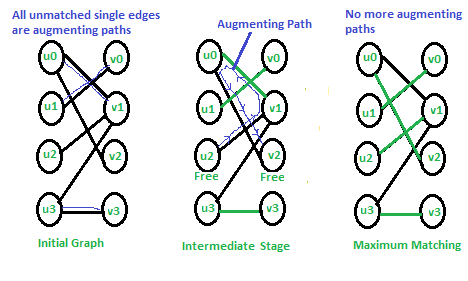
El siguiente diagrama muestra el funcionamiento del algoritmo.
En el gráfico inicial, todos los bordes individuales son caminos crecientes y podemos seleccionarlos en cualquier orden. En la etapa intermedia, solo hay un camino de aumento. Eliminamos los bordes coincidentes de este camino de M y agregamos los bordes que no coinciden. En la coincidencia final, no hay rutas de aumento, por lo que la coincidencia es máxima.
La implementación del algoritmo Hopcroft Karp se analiza en el conjunto 2.
Algoritmo Hopcroft-Karp para coincidencia máxima | Conjunto 2 (Implementación)
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA