Algoritmos aleatorios | Conjunto 0 (Antecedentes matemáticos)

Probabilidad condicional La probabilidad condicional P(A | B) indica la probabilidad de que suceda incluso ‘A’ dado que ocurrió el par B.

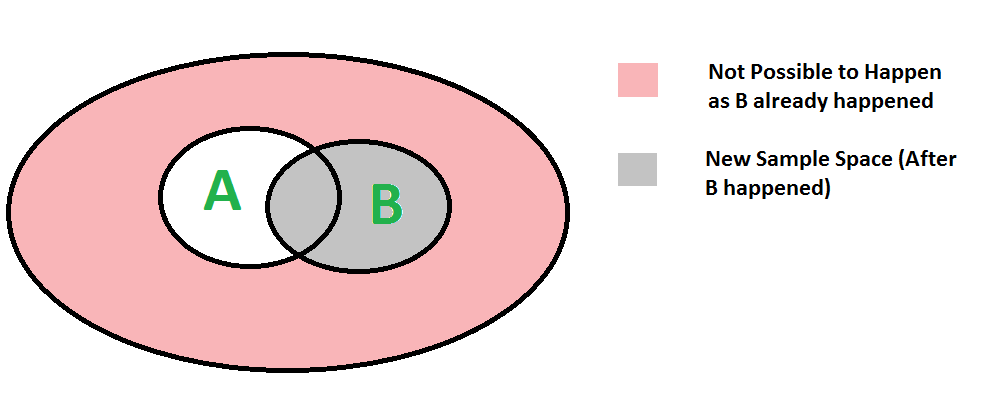
Podemos entender fácilmente la fórmula anterior usando el diagrama a continuación. Como B ya sucedió, el espacio muestral se reduce a B. Entonces, la probabilidad de que A suceda se convierte en P(A ∩ B) dividida por P(B) 

A continuación se muestra la fórmula de Bayes para la probabilidad condicional. 

La fórmula proporciona una relación entre P(A|B) y P(B|A). Se deriva principalmente de la fórmula de probabilidad condicional discutida en la publicación anterior . 

Considere las siguientes fórmulas para las probabilidades condicionales P(A|B) y P(B|A) 

Dado que P(B ∩ A) = P(A ∩ B), podemos reemplazar P(A ∩ B) en la primera fórmula con P(B|A)P(A) 
Después de reemplazar, obtenemos la fórmula dada. Consulte esto para ver ejemplos de la fórmula de Bayes. 

Variables aleatorias: 
una variable aleatoria es en realidad una función que asigna el resultado de un evento aleatorio (como el lanzamiento de una moneda) a un valor real. 

Ejemplo : 

Coin tossing game : 
A player pays 50 bucks if result of coin
toss is "Head" 

The person gets 50 bucks if the result is
Tail. 

A random variable profit for person can 
be defined as below : 

Profit = +50 if Head
         -50 if Tail  

Generally gambling games are not fair for players, 
the organizer takes a share of profit for all 
arrangements. So expected profit is negative for 
a player in gambling and positive for the organizer. 
That is how organizers make money.

Valor esperado de la variable aleatoria: 
el valor esperado de una variable aleatoria R se puede definir de la siguiente manera

    E[R] = r1*p1 + r2*p2 + ... rk*pk 
    
    ri ==> Value of R with probability pi

El valor esperado es básicamente la suma del producto de los siguientes dos términos (para todos los eventos posibles) 
a) Probabilidad de un evento. 
b) Valor de R en ese par 

Example 1:
In above example of coin toss,
Expected value of profit = 50 * (1/2) + 
                          (-50) * (1/2)
                         = 0

Example 2:
Expected value of six faced dice throw is 
  = 1*(1/6) + 2*(1/6) + .... + 6*(1/6)
  = 3.5

Linealidad de la expectativa: 
Sean R ₁ y R ₂ dos variables aleatorias discretas en algún espacio de probabilidad, entonces 

     E[R1 + R2] = E[R1] + E[R2] 

Por ejemplo, el valor esperado de la suma de 3 lanzamientos de dados es = 3 * 7/2 = 7 

Consulte esto para obtener una explicación más detallada y ejemplos. 

Número esperado de intentos hasta el éxito 
Si la probabilidad de éxito es p en cada intento, entonces el número esperado de intentos hasta el éxito es 1/p. Por ejemplo, considere que se lanza un dado justo de 6 caras hasta que se ve un ‘5’ como resultado del lanzamiento de dados. El número esperado de lanzamientos antes de ver un 5 es 6. Tenga en cuenta que 1/6 es la probabilidad de obtener un 5 en cada intento. Entonces, el número de intentos es 1/(1/6) = 6. 
Como otro ejemplo, considere una versión QuickSort que sigue buscando pivotes hasta que se elige uno de los n/2 elementos del medio. El tiempo esperado de intentos para encontrar el pivote central sería 2, ya que la probabilidad de elegir uno de los n/2 elementos centrales es 1/2. Este ejemplo se analiza con más detalle en el Conjunto 1 . 
Consulte esto para obtener una explicación más detallada y ejemplos. 

Más sobre algoritmos aleatorios: 

• Algoritmos aleatorios | Conjunto 1 (Introducción y Análisis)
• Algoritmos aleatorios | Conjunto 2 (Clasificación y Aplicaciones)
• Algoritmos aleatorios | Conjunto 3 (1/2 mediana aproximada)

Todos los temas de algoritmos aleatorios 

Este artículo es una contribución de Shivam Gupta . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.