Algoritmos | Análisis de Algoritmos (Recurrencias) | Pregunta 11 – Part 1

Considere la siguiente recurrencia:

¿Cuál de las siguientes es verdadera?

(A) T(n) = (loglogn)
(B) T(n) = (logn)
(C) T(n) = (raíz cuadrada(n))
(D) T(n) = (n)

(A) A
(B) B
(C) C
(D) D

Respuesta: (B)
Explicación: Esta pregunta se puede resolver primero cambiando la variable y luego el Método Maestro.

  Let n = 2^m
  T(2^m) = T(2^(m/2)) + 1
  Let T(2^m) =  S(m)
  S(m)  = 2S(m/2) + 1  

La expresión anterior es una recursión transversal de un árbol binario cuya complejidad temporal es (m). También puedes probar usando el teorema de Master .

S(m)  = (m)  
      = (logn)  /* Since n = 2^m */

Ahora, volvamos a la función recursiva original T(n)

  T(n)  = T(2^m) = S(m)
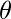                 = (Logn)

Cuestionario de esta pregunta