Se nos da un árbol de tamaño n como array padre[0..n-1] donde cada índice i en el padre[] representa un Node y el valor en i representa el padre inmediato de ese Node. Para el valor del Node raíz será -1. Encuentre la altura del árbol genérico dados los enlaces principales.
Ejemplos:
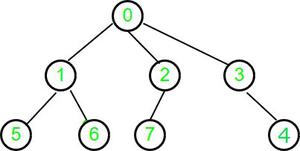
Input : parent[] = {-1, 0, 0, 0, 3, 1, 1, 2}
Output : 2
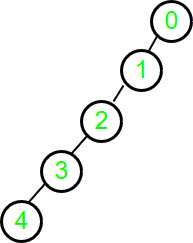
Input : parent[] = {-1, 0, 1, 2, 3}
Output : 4
Enfoque 1:
una solución es atravesar el árbol desde el Node hasta que se alcanza el Node raíz con el valor de Node -1. Mientras que Atravesar para cada Node almacena la longitud máxima de la ruta.
La complejidad temporal de esta solución es O(n^2) .
Enfoque 2:
construya un gráfico para el árbol N-ario en el tiempo O (n) y aplique BFS en el gráfico almacenado en el tiempo O (n) y mientras realiza el nivel máximo alcanzado de la tienda BFS. Esta solución hace dos iteraciones para encontrar la altura del árbol N-ario.
C++
// C++ code to find height of N-ary
// tree in O(n)
#include <bits/stdc++.h>
#define MAX 1001
using namespace std;
// Adjacency list to
// store N-ary tree
vector<int> adj[MAX];
// Build tree in tree in O(n)
int build_tree(int arr[], int n)
{
int root_index = 0;
// Iterate for all nodes
for (int i = 0; i < n; i++) {
// if root node, store index
if (arr[i] == -1)
root_index = i;
else {
adj[i].push_back(arr[i]);
adj[arr[i]].push_back(i);
}
}
return root_index;
}
// Applying BFS
int BFS(int start)
{
// map is used as visited array
map<int, int> vis;
queue<pair<int, int> > q;
int max_level_reached = 0;
// height of root node is zero
q.push({ start, 0 });
// p.first denotes node in adjacency list
// p.second denotes level of p.first
pair<int, int> p;
while (!q.empty()) {
p = q.front();
vis[p.first] = 1;
// store the maximum level reached
max_level_reached = max(max_level_reached,
p.second);
q.pop();
for (int i = 0; i < adj[p.first].size(); i++)
// adding 1 to previous level
// stored on node p.first
// which is parent of node adj[p.first][i]
// if adj[p.first][i] is not visited
if (!vis[adj[p.first][i]])
q.push({ adj[p.first][i], p.second + 1 });
}
return max_level_reached;
}
// Driver Function
int main()
{
// node 0 to node n-1
int parent[] = { -1, 0, 1, 2, 3 };
// Number of nodes in tree
int n = sizeof(parent) / sizeof(parent[0]);
int root_index = build_tree(parent, n);
int ma = BFS(root_index);
cout << "Height of N-ary Tree=" << ma;
return 0;
}
Java
// Java code to find height of N-ary
// tree in O(n)
import java.io.*;
import java.util.*;
class GFG
{
static int MAX = 1001;
// Adjacency list to
// store N-ary tree
static ArrayList<ArrayList<Integer>> adj =
new ArrayList<ArrayList<Integer>>();
// Build tree in tree in O(n)
static int build_tree(int arr[], int n)
{
int root_index = 0;
// Iterate for all nodes
for (int i = 0; i < n; i++)
{
// if root node, store index
if (arr[i] == -1)
root_index = i;
else
{
adj.get(i).add(arr[i]);
adj.get(arr[i]).add(i);
}
}
return root_index;
}
// Applying BFS
static int BFS(int start)
{
// map is used as visited array
Map<Integer, Integer> vis = new HashMap<Integer, Integer>();
ArrayList<ArrayList<Integer>> q = new ArrayList<ArrayList<Integer>>();
int max_level_reached = 0;
// height of root node is zero
q.add(new ArrayList<Integer>(Arrays.asList(start, 0 )));
// p.first denotes node in adjacency list
// p.second denotes level of p.first
ArrayList<Integer> p = new ArrayList<Integer>();
while(q.size() != 0)
{
p = q.get(0);
vis.put(p.get(0),1);
// store the maximum level reached
max_level_reached = Math.max(max_level_reached,p.get(1));
q.remove(0);
for(int i = 0; i < adj.get(p.get(0)).size(); i++)
{
// adding 1 to previous level
// stored on node p.first
// which is parent of node adj[p.first][i]
// if adj[p.first][i] is not visited
if(!vis.containsKey(adj.get(p.get(0)).get(i)))
{
q.add(new ArrayList<Integer>(Arrays.asList(adj.get(p.get(0)).get(i), p.get(1)+1)));
}
}
}
return max_level_reached;
}
// Driver Function
public static void main (String[] args)
{
for(int i = 0; i < MAX; i++)
{
adj.add(new ArrayList<Integer>());
}
// node 0 to node n-1
int parent[] = { -1, 0, 1, 2, 3 };
// Number of nodes in tree
int n = parent.length;
int root_index = build_tree(parent, n);
int ma = BFS(root_index);
System.out.println( "Height of N-ary Tree=" + ma);
}
}
// This code is contributed by rag2127
Python3
# Python3 code to find height
# of N-ary tree in O(n)
from collections import deque
MAX = 1001
# Adjacency list to
# store N-ary tree
adj = [[] for i in range(MAX)]
# Build tree in tree in O(n)
def build_tree(arr, n):
root_index = 0
# Iterate for all nodes
for i in range(n):
# if root node, store
# index
if (arr[i] == -1):
root_index = i
else:
adj[i].append(arr[i])
adj[arr[i]].append(i)
return root_index
# Applying BFS
def BFS(start):
# map is used as visited
# array
vis = {}
q = deque()
max_level_reached = 0
# height of root node is
# zero
q.append([start, 0])
# p.first denotes node in
# adjacency list
# p.second denotes level of
# p.first
p = []
while (len(q) > 0):
p = q.popleft()
vis[p[0]] = 1
# store the maximum level
# reached
max_level_reached = max(max_level_reached,
p[1])
for i in range(len(adj[p[0]])):
# adding 1 to previous level
# stored on node p.first
# which is parent of node
# adj[p.first][i]
# if adj[p.first][i] is not visited
if (adj[p[0]][i] not in vis ):
q.append([adj[p[0]][i],
p[1] + 1])
return max_level_reached
# Driver code
if __name__ == '__main__':
# node 0 to node n-1
parent = [-1, 0, 1, 2, 3]
# Number of nodes in tree
n = len(parent)
root_index = build_tree(parent, n)
ma = BFS(root_index)
print("Height of N-ary Tree=",
ma)
# This code is contributed by Mohit Kumar 29
C#
// C# code to find height of N-ary
// tree in O(n)
using System;
using System.Collections.Generic;
public class GFG
{
static int MAX = 1001;
// Adjacency list to
// store N-ary tree
static List<List<int>> adj = new List<List<int>>();
// Build tree in tree in O(n)
static int build_tree(int[] arr, int n)
{
int root_index = 0;
// Iterate for all nodes
for (int i = 0; i < n; i++)
{
// if root node, store index
if (arr[i] == -1)
root_index = i;
else
{
adj[i].Add(arr[i]);
adj[arr[i]].Add(i);
}
}
return root_index;
}
// Applying BFS
static int BFS(int start)
{
// map is used as visited array
Dictionary<int, int> vis = new Dictionary<int, int>();
List<List<int>> q= new List<List<int>>();
int max_level_reached = 0;
// height of root node is zero
q.Add(new List<int>(){start, 0});
// p.first denotes node in adjacency list
// p.second denotes level of p.first
List<int> p = new List<int>();
while(q.Count != 0)
{
p = q[0];
vis.Add(p[0], 1);
// store the maximum level reached
max_level_reached = Math.Max(max_level_reached, p[1]);
q.RemoveAt(0);
for(int i = 0; i < adj[p[0]].Count; i++)
{
// adding 1 to previous level
// stored on node p.first
// which is parent of node adj[p.first][i]
// if adj[p.first][i] is not visited
if(!vis.ContainsKey(adj[p[0]][i]))
{
q.Add(new List<int>(){adj[p[0]][i], p[1] + 1 });
}
}
}
return max_level_reached;
}
// Driver Function
static public void Main ()
{
for(int i = 0; i < MAX; i++)
{
adj.Add(new List<int>());
}
// node 0 to node n-1
int[] parent = { -1, 0, 1, 2, 3 };
// Number of nodes in tree
int n = parent.Length;
int root_index = build_tree(parent, n);
int ma = BFS(root_index);
Console.Write("Height of N-ary Tree=" + ma);
}
}
// This code is contributed by avanitrachhadiya2155
Javascript
<script>
// JavaScript code to find height of N-ary
// tree in O(n)
let MAX = 1001;
let adj = [];
// Adjacency list to
// store N-ary tree
function build_tree(arr,n)
{
let root_index = 0;
// Iterate for all nodes
for (let i = 0; i < n; i++)
{
// if root node, store index
if (arr[i] == -1)
root_index = i;
else
{
adj[i].push(arr[i]);
adj[arr[i]].push(i);
}
}
return root_index;
}
// Applying BFS
function BFS(start)
{
// map is used as visited array
let vis = new Map();
let q = [];
let max_level_reached = 0;
// height of root node is zero
q.push([start, 0 ]);
// p.first denotes node in adjacency list
// p.second denotes level of p.first
let p = [];
while(q.length != 0)
{
p = q[0];
vis.set(p[0],1);
// store the maximum level reached
max_level_reached =
Math.max(max_level_reached,p[1]);
q.shift();
for(let i = 0; i < adj[p[0]].length; i++)
{
// adding 1 to previous level
// stored on node p.first
// which is parent of node adj[p.first][i]
// if adj[p.first][i] is not visited
if(!vis.has(adj[p[0]][i]))
{
q.push([adj[p[0]][i], p[1]+1]);
}
}
}
return max_level_reached;
}
// Driver Function
for(let i = 0; i < MAX; i++)
{
adj.push([]);
}
// node 0 to node n-1
let parent = [ -1, 0, 1, 2, 3 ];
// Number of nodes in tree
let n = parent.length;
let root_index = build_tree(parent, n);
let ma = BFS(root_index);
document.write( "Height of N-ary Tree=" + ma);
// This code is contributed by unknown2108
</script>
Height of N-ary Tree=4
La complejidad temporal de esta solución es O(2n) que converge a O(n) para n muy grande.
Enfoque 3:
podemos encontrar la altura del árbol N-ario en una sola iteración. Visitamos los Nodes del 0 al n-1 de forma iterativa y marcamos recursivamente los ancestros no visitados si no han sido visitados antes hasta llegar a un Node visitado o al Node raíz. Si alcanzamos el Node visitado mientras recorremos el árbol usando enlaces principales, entonces usamos su altura y no avanzaremos más en la recursividad.
Explicación para el ejemplo 1::

Para el Node 0 : verifique que el Node raíz sea verdadero,
devuelva 0 como altura, marque el Node 0 como visitado
Para el Node 1 : recurra a un ancestro inmediato, es decir, 0, que ya se visitó
Entonces, use su altura y devuelva la altura (Node 0) +1
Marcar el Node 1 como visitado
Para el Node 2 : recurrencia para un ancestro inmediato, es decir, 0, que ya se visitó
Entonces, use su altura y devuelva la altura (Node 0) +1
Marcar el Node 2 como visitado
Para el Node 3 : recurrencia para un antecesor inmediato, es decir, 0, que ya ha sido visitado
Por lo tanto, use su altura y devuelva la altura (Node 0) +1
Marque el Node 3 como visitado
Para el Node 4: recurrencia para un antepasado inmediato, es decir, 3, que ya se visitó
Entonces, use su altura y devuelva altura (Node 3) +1
Marcar el Node 3 como visitado
Para el Node 5 : recurrencia para un antepasado inmediato, es decir, 1, que ya se visitó
Por lo tanto, use su altura y la altura de retorno (Node 1) +1
Marque el Node 5 como visitado
Para el Node 6 : se repite para un ancestro inmediato, es decir, 1, que ya se visitó
Entonces, use su altura y la altura de retorno (Node 1) +1
Marcar el Node 6 como visitado
Para el Node 7 : recurrencia para un ancestro inmediato, es decir, 2, que ya se visitó
Entonces, use su altura y devuelva la altura (Node 2) +1
Marque el Node 7 como visitado
Por lo tanto, procesamos cada Node en el árbol N-ario solo una vez.
C++
// C++ code to find height of N-ary
// tree in O(n) (Efficient Approach)
#include <bits/stdc++.h>
using namespace std;
// Recur For Ancestors of node and
// store height of node at last
int fillHeight(int p[], int node, int visited[],
int height[])
{
// If root node
if (p[node] == -1) {
// mark root node as visited
visited[node] = 1;
return 0;
}
// If node is already visited
if (visited[node])
return height[node];
// Visit node and calculate its height
visited[node] = 1;
// recur for the parent node
height[node] = 1 + fillHeight(p, p[node],
visited, height);
// return calculated height for node
return height[node];
}
int findHeight(int parent[], int n)
{
// To store max height
int ma = 0;
// To check whether or not node is visited before
int visited[n];
// For Storing Height of node
int height[n];
memset(visited, 0, sizeof(visited));
memset(height, 0, sizeof(height));
for (int i = 0; i < n; i++) {
// If not visited before
if (!visited[i])
height[i] = fillHeight(parent, i,
visited, height);
// store maximum height so far
ma = max(ma, height[i]);
}
return ma;
}
// Driver Function
int main()
{
int parent[] = { -1, 0, 0, 0, 3, 1, 1, 2 };
int n = sizeof(parent) / sizeof(parent[0]);
cout << "Height of N-ary Tree = "
<< findHeight(parent, n);
return 0;
}
Java
// Java code to find height of N-ary
// tree in O(n) (Efficient Approach)
import java.util.*;
class GFG
{
// Recur For Ancestors of node and
// store height of node at last
static int fillHeight(int p[], int node,
int visited[], int height[])
{
// If root node
if (p[node] == -1)
{
// mark root node as visited
visited[node] = 1;
return 0;
}
// If node is already visited
if (visited[node] == 1)
return height[node];
// Visit node and calculate its height
visited[node] = 1;
// recur for the parent node
height[node] = 1 + fillHeight(p, p[node],
visited, height);
// return calculated height for node
return height[node];
}
static int findHeight(int parent[], int n)
{
// To store max height
int ma = 0;
// To check whether or not node is visited before
int []visited = new int[n];
// For Storing Height of node
int []height = new int[n];
for(int i = 0; i < n; i++)
{
visited[i] = 0;
height[i] = 0;
}
for (int i = 0; i < n; i++)
{
// If not visited before
if (visited[i] != 1)
height[i] = fillHeight(parent, i,
visited, height);
// store maximum height so far
ma = Math.max(ma, height[i]);
}
return ma;
}
// Driver Code
public static void main(String[] args)
{
int parent[] = { -1, 0, 0, 0, 3, 1, 1, 2 };
int n = parent.length;
System.out.println("Height of N-ary Tree = " +
findHeight(parent, n));
}
}
// This code is contributed by 29AjayKumar
Python3
# Python3 code to find height of N-ary
# tree in O(n) (Efficient Approach)
# Recur For Ancestors of node and
# store height of node at last
def fillHeight(p, node, visited, height):
# If root node
if (p[node] == -1):
# mark root node as visited
visited[node] = 1
return 0
# If node is already visited
if (visited[node]):
return height[node]
# Visit node and calculate its height
visited[node] = 1
# recur for the parent node
height[node] = 1 + fillHeight(p, p[node],
visited, height)
# return calculated height for node
return height[node]
def findHeight(parent, n):
# To store max height
ma = 0
# To check whether or not node is
# visited before
visited = [0] * n
# For Storing Height of node
height = [0] * n
for i in range(n):
# If not visited before
if (not visited[i]):
height[i] = fillHeight(parent, i,
visited, height)
# store maximum height so far
ma = max(ma, height[i])
return ma
# Driver Code
if __name__ == '__main__':
parent = [-1, 0, 0, 0, 3, 1, 1, 2]
n = len(parent)
print("Height of N-ary Tree =",
findHeight(parent, n))
# This code is contributed by PranchalK
C#
// C# code to find height of N-ary
// tree in O(n) (Efficient Approach)
using System;
class GFG
{
// Recur For Ancestors of node and
// store height of node at last
static int fillHeight(int []p, int node,
int []visited,
int []height)
{
// If root node
if (p[node] == -1)
{
// mark root node as visited
visited[node] = 1;
return 0;
}
// If node is already visited
if (visited[node] == 1)
return height[node];
// Visit node and calculate its height
visited[node] = 1;
// recur for the parent node
height[node] = 1 + fillHeight(p, p[node],
visited, height);
// return calculated height for node
return height[node];
}
static int findHeight(int []parent, int n)
{
// To store max height
int ma = 0;
// To check whether or not
// node is visited before
int []visited = new int[n];
// For Storing Height of node
int []height = new int[n];
for(int i = 0; i < n; i++)
{
visited[i] = 0;
height[i] = 0;
}
for (int i = 0; i < n; i++)
{
// If not visited before
if (visited[i] != 1)
height[i] = fillHeight(parent, i,
visited, height);
// store maximum height so far
ma = Math.Max(ma, height[i]);
}
return ma;
}
// Driver Code
public static void Main(String[] args)
{
int []parent = { -1, 0, 0, 0, 3, 1, 1, 2 };
int n = parent.Length;
Console.WriteLine("Height of N-ary Tree = " +
findHeight(parent, n));
}
}
// This code contributed by Rajput-Ji
Javascript
<script>
// Javascript code to find height of N-ary
// tree in O(n) (Efficient Approach)
// Recur For Ancestors of node and
// store height of node at last
function fillHeight(p, node, visited, height)
{
// If root node
if (p[node] == -1)
{
// mark root node as visited
visited[node] = 1;
return 0;
}
// If node is already visited
if (visited[node] == 1)
return height[node];
// Visit node and calculate its height
visited[node] = 1;
// recur for the parent node
height[node] = 1 + fillHeight(p, p[node],
visited, height);
// return calculated height for node
return height[node];
}
function findHeight(parent,n)
{
// To store max height
let ma = 0;
// To check whether or not node is visited before
let visited = new Array(n);
// For Storing Height of node
let height = new Array(n);
for(let i = 0; i < n; i++)
{
visited[i] = 0;
height[i] = 0;
}
for (let i = 0; i < n; i++)
{
// If not visited before
if (visited[i] != 1)
height[i] = fillHeight(parent, i,
visited, height);
// store maximum height so far
ma = Math.max(ma, height[i]);
}
return ma;
}
// Driver Code
let parent = [ -1, 0, 0, 0, 3, 1, 1, 2 ];
let n = parent.length;
document.write("Height of N-ary Tree = " +
findHeight(parent, n));
// This code is contributed by ab2127
</script>
Height of N-ary Tree = 2
Complejidad de tiempo: O(n)
Publicación traducida automáticamente
Artículo escrito por Abhishek rajput y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA