Ambigüedad en gramática libre de contexto y lenguajes libres de contexto

Requisito previo: autómatas pushdown y lenguajes libres de contexto . 

Supongamos que tenemos una gramática libre de contexto G con reglas de producción: S->aSb|bSa|SS|ℇ 
 

Derivación más a la izquierda (LMD) y árbol de derivación: la derivación más a la izquierda de una string desde el símbolo inicial S se realiza reemplazando el símbolo no terminal más a la izquierda por RHS de la regla de producción correspondiente. Por ejemplo: la derivación más a la izquierda de la string abab de la gramática G anterior se realiza como:

 S => aSb => abSab => abab

Los símbolos subrayados se reemplazan usando reglas de producción. 

Árbol de derivación: indica cómo se deriva la string utilizando las reglas de producción de S y se muestra en la Figura 1. 

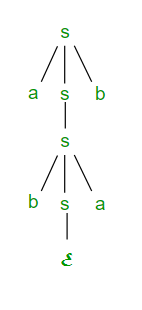
Figura 1

Derivación más a la derecha (RMD): la derivación más a la derecha de una string desde el símbolo inicial S se realiza reemplazando el símbolo no terminal más a la derecha por RHS de la regla de producción correspondiente. Por ejemplo: la derivación más a la derecha de la string abab de la gramática G anterior se realiza como: 
 

S => SS => SaSb => Sab => aSbab => abab

Los símbolos subrayados se reemplazan usando reglas de producción. El árbol de derivación para abab usando la derivación más a la derecha se muestra en la Figura 2. 
 

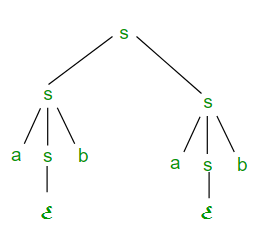
Figura 2

Una derivación puede ser LMD o RMD o ambas o ninguna. Por ejemplo: 
 

S => aSb => abSab => abab is LMD as well as RMD

but S => SS => SaSb => Sab => aSbab => abab is RMD but not LMD.

Gramática libre de contexto ambigua: una gramática libre de contexto se denomina ambigua si existe más de un LMD o más de un RMD para una string generada por la gramática. También habrá más de un árbol de derivación para una string en gramática ambigua. La gramática descrita anteriormente es ambigua porque hay dos árboles de derivación (Figura 1 y Figura 2). Puede haber más de un RMD para la string abab, que son:

S => SS => SaSb => Sab => aSbab => abab

S => aSb => abSab => abab

Lenguajes libres de contexto ambiguos: un lenguaje libre de contexto se denomina ambiguo si no existe una gramática inequívoca para definir ese lenguaje y también se denomina lenguajes libres de contexto inherentemente ambiguos. 

Nota: 
 

• Si una gramática libre de contexto G es ambigua, el lenguaje generado por la gramática L(G) puede o no ser ambiguo
• No siempre es posible convertir CFG ambigua en CFG inequívoca. Solo algunos CFG ambiguos se pueden convertir en CFG no ambiguos.
• No existe un algoritmo para convertir CFG ambiguo en CFG inequívoco.
• Siempre existe un CFG inequívoco correspondiente a CFL inequívoco.
• Los CFL deterministas siempre son inequívocos.

Pregunta: Considere las siguientes afirmaciones sobre la gramática libre de contexto 
 

G = {S->SS, S->ab, S->ba, S->ℇ}

• I G es ambiguo
• II G produce todas las strings con el mismo número de a y b
• III G puede ser aceptado por un PDA determinista

¿Cuál de las siguientes combinaciones expresa todas las afirmaciones verdaderas sobre G? 
 

1. yo solo
2. I y III solamente
3. II y III solamente
4. I, II y III

Solución: Hay diferentes LMD para string abab que pueden ser 
 

S => SS => SSS => abSS => ababS => abab

S => SS => abS => abab

Así que la gramática es ambigua. Entonces la afirmación I es verdadera. 

La declaración II establece que la gramática G produce todas las strings con el mismo número de a y b, pero no puede generar una string aabb. Entonces la declaración II es incorrecta. 

La declaración III también es correcta ya que puede ser aceptada por PDA determinista. Entonces la opción correcta es (B). 

Pregunta: ¿Cuál de las siguientes afirmaciones es FALSA? 
 

1. Existen lenguajes libres de contexto tales que todas las gramáticas libres de contexto que los generan son ambiguas.
2. Una gramática libre de contexto inequívoca siempre tiene un árbol de análisis único para cada string del lenguaje generado por ella.
3. Tanto los autómatas pushdown deterministas como los no deterministas siempre aceptan el mismo conjunto de lenguajes.
4. Un conjunto finito de strings de un alfabeto es siempre un lenguaje regular.

Solución: (A) es correcta porque para CFL ambiguas, todas las CFG correspondientes son ambiguas. 

(B) también es correcto, ya que CFG inequívoco tiene un árbol de análisis único para cada string del idioma generado por él. 

(C) es falso ya que algunos lenguajes son aceptados por PDA no determinista pero no por PDA determinista. 

(D) también es cierto ya que el conjunto finito de strings siempre es regular. 

Entonces la opción (C) es la opción correcta. 
 

Este artículo es una contribución de Sonal Tuteja. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.