La idea principal del análisis asintótico es tener una medida de la eficiencia de los algoritmos que no dependen de las constantes específicas de la máquina, principalmente porque este análisis no requiere que se implementen algoritmos ni que los programas tomen tiempo para compararlos. Ya hemos discutido tres notaciones asintóticas principales . Las siguientes 2 notaciones asintóticas más se utilizan para representar la complejidad temporal de los algoritmos.
Pequeña notación asintótica
Big-Ο se usa como un límite superior estricto en el crecimiento del esfuerzo de un algoritmo (este esfuerzo se describe mediante la función f (n)), aunque, tal como está escrito, también puede ser un límite superior flexible. La notación “pequeña-o” (o()) se usa para describir un límite superior que no puede ser ajustado.
Definición: Sean f(n) y g(n) funciones que transforman enteros positivos en números reales positivos. Decimos que f(n) es ο(g(n)) (o f(n) Ε ο(g(n))) si para cualquier constante real c > 0, existe una constante entera n0 ≥ 1 tal que 0 ≤ f(n) < c*g(n).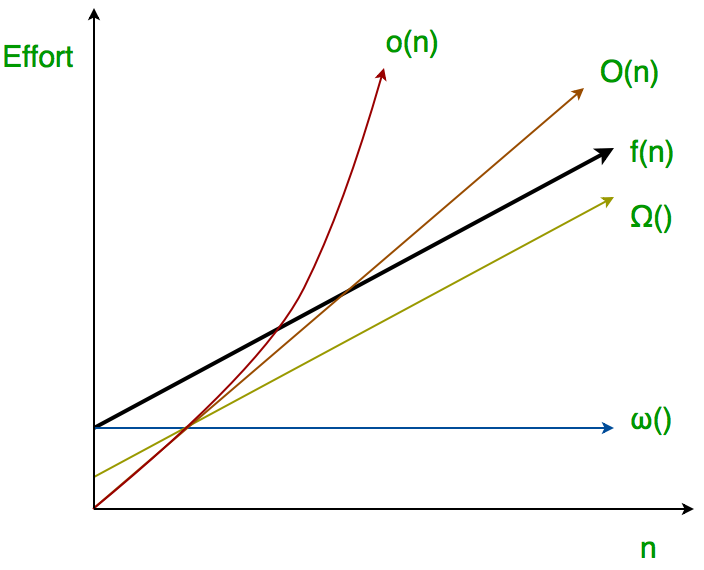
Por lo tanto, little o() significa un límite superior flexible de f(n). Little o es una estimación aproximada del orden máximo de crecimiento, mientras que Big-Ο puede ser el orden real de crecimiento.
En relación matemática, f(n) = o(g(n)) significa lim f(n)/g(n) = 0 n→∞
Ejemplos:
¿Es 7n + 8 ∈ o(n 2 )?
Para que eso sea cierto, para cualquier c, tenemos que ser capaces de encontrar un n0 que haga
f(n) < c * g(n) asintóticamente cierto.
tomemos un ejemplo,
Si c = 100, comprobamos que la desigualdad es claramente cierta. Si c = 1/100 , tendremos que usar
un poco más de imaginación, pero podremos encontrar un n0. (Pruebe n0 = 1000.) Desde
estos ejemplos, la conjetura parece ser correcta.
luego verifique los límites,
lím f(n)/g(n) = lím (7n + 8)/(n 2 ) = lím 7/2n = 0 (l’hospital)
norte→∞ norte→∞ norte→∞
por lo tanto 7n + 8 ∈ o(n 2 )
Pequeña notación asintótica ω
Definición: Sean f(n) y g(n) funciones que transforman enteros positivos en números reales positivos. Decimos que f(n) es ω(g(n)) (o f(n) ∈ ω(g(n))) si para cualquier constante real c > 0, existe una constante entera n0 ≥ 1 tal que f (n) > c * g(n) ≥ 0 para todo entero n ≥ n0.
f(n) tiene una tasa de crecimiento más alta que g(n), por lo que la principal diferencia entre Big Omega (Ω) y little omega (ω) radica en sus definiciones. En el caso de Big Omega f(n)=Ω(g(n )) y el límite es 0<=cg(n)<=f(n), pero en el caso de omega pequeño, es cierto para 0<=c*g(n)<f(n).
La relación entre Big Omega (Ω) y Little Omega (ω) es similar a la de Big-Ο y Little o excepto que ahora estamos viendo los límites inferiores. Little Omega (ω) es una estimación aproximada del orden de crecimiento, mientras que Big Omega (Ω) puede representar el orden exacto de crecimiento. Usamos la notación ω para denotar un límite inferior que no es asintóticamente estrecho. Y, f(n) ∈ ω(g(n)) si y solo si g(n) ∈ ο((f(n)).
En relación matemática,
si f(n) ∈ ω(g(n)) entonces,
lím f(n)/g(n) = ∞
n→∞
Ejemplo:
Demostrar que 4n + 6 ∈ ω(1);
el pequeño tiempo de ejecución omega(ο) se puede probar aplicando la fórmula de límite que se indica a continuación.
si lim f(n)/g(n) = ∞ entonces la función f(n) es ω(g(n))
n→∞
aquí tenemos funciones f(n)=4n+6 y g(n)=1
lím (4n+6)/(1) = ∞
n→∞
y también para cualquier c podemos obtener n0 para esta desigualdad 0 <= c*g(n) < f(n), 0 <= c*1 < 4n+6
Por lo tanto probado.
Este artículo es una contribución de Kadam Patel . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA