Distribución de datos:
La distribución de un conjunto de datos estadísticos (o una población) es una lista o función que muestra todos los valores posibles (o intervalos) de los datos y con qué frecuencia ocurren, podemos pensar en una distribución como una función que describe la relación entre las observaciones en un espacio muestral.
Ejemplo:
Se midió la vida útil de 800 dispositivos eléctricos. Debido a que los tiempos de vida tenían muchos valores diferentes, las mediciones se agruparon en 50 intervalos, o clases, de 10 horas cada uno:
601 a 610 horas, 611 a 620 horas, y así sucesivamente, hasta 1.091 a 1.100 horas. La distribución de frecuencia relativa resultante, como histograma, tiene 50 barras delgadas y muchas alturas de barra diferentes, como se muestra en la figura de análisis de datos a continuación.

La frecuencia relativa es la frecuencia con la que sucede algo dividido por todos los resultados. Como ejemplo aquí, se puede considerar como el número de dispositivos eléctricos con una vida útil de (Ex 601 a 610) dividido por el total de dispositivos.
En el histograma, la mediana está representada por M, la media está representada por my la desviación estándar está representada por d.
- La mediana, representada por M, está entre 730 y 740
- La media, representada por m, está entre 750 y 760
- La suma de las áreas de las 50 barras de frecuencia relativa es 1
Los histogramas que representan conjuntos de datos muy grandes agrupados en muchas clases tienen una apariencia relativamente suave. En consecuencia, la distribución se puede modelar mediante una curva suave que está cerca de la parte superior de las barras. Esta curva se llama curva de distribución.
El propósito de la curva de distribución es dar una buena ilustración de una gran distribución de datos numéricos que no depende de clases específicas. La propiedad de la curva de distribución es que el área bajo la curva en cualquier corte vertical, al igual que una barra de histograma, representa la proporción de los datos que se encuentran en el intervalo correspondiente en el eje horizontal.
Variable aleatoria:
Una variable aleatoria puede asignar cada valor del espacio muestral a un número real y, además, la suma de los valores del número real siempre es igual a 1.
Ejemplo:
En un experimento se lanzan al aire tres monedas justas, luego el espacio muestral es
S = { HHH, HHT, HTH, THH, HTT, TTH, THT, TTT}
Deje que la variable X cuente la cantidad de veces que aparece la cabeza, por lo tanto, la llamamos variable aleatoria. Además, la variable aleatoria generalmente está representada por X.
Ahora, X puede tomar valores 3, 2, 1, 0
P(X = 1) is probability of occurring head one time, P(X = 1) = P(THT) + P(TTH) + P(HTT) = 3/8
Tipos de variable aleatoria:
- Variable aleatoria discreta:
una variable que puede tomar un valor de un conjunto discreto de valores.Ejemplo:
Sea x la suma de dados, ahora x es una variable aleatoria discreta ya que puede tomar un valor del conjunto {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, ya que la suma de dos dados solo puede dar uno de estos valores. - Variable aleatoria continua:
una variable que puede tomar un valor de un rango continuo de valores.Ejemplo:
x denota el volumen de agua en una taza de 500 ml. Ahora x puede ser un número de 0 a 500, cualquiera de los cuales valor, puede tomar x.
Distribución de probabilidad:
Las distribuciones de probabilidad indican la probabilidad de un evento o resultado.
P(x) = la probabilidad de que la variable aleatoria tome un valor específico de x.
Ejemplo:
En un experimento se lanzan al aire tres monedas justas, entonces el espacio muestral es,
S = {HHH, HHT, HTH, THH, HTT, TTH, THT, TTT}
X es una variable aleatoria que tiene valores 3, 2, 1, 0 entonces
P(X = 0) = P(TTT) = 1/8 P(X = 1) = P(HTT) + P(TTH) + P(THT) = 3/8 P(X = 2) = P(HHT) + P(HTH) + P(THH) = 3/8 P(X = 3) = P(HHH) = 1/8
Por lo tanto,
| X (variable aleatoria) | P(X) |
|---|---|
| 0 | 1/8 |
| 1 | 3/8 |
| 2 | 3/8 |
| 3 | 1/8 |
Esta tabla se llama distribución de probabilidad de la variable aleatoria X.
La distribución se puede dividir en 2 tipos :
- Distribución discreta:
basada en una variable aleatoria discreta, los ejemplos son la distribución binomial, la distribución de Poisson. - Distribución continua:
basada en variables aleatorias continuas, los ejemplos son distribución normal, distribución uniforme, distribución exponencial.
Función de masa de probabilidad:
Sea x una variable aleatoria discreta, entonces su función de masa de probabilidad p(x) se define de tal manera que
1. p(x)0 2.
= 1 3. p(x) = P(X=x)
Función de densidad de probabilidad:
Sea x una variable aleatoria continua, entonces la función de densidad de probabilidad F(x) se define tal que
1. F(x)0 2.
= 1 3. P(a < x < b) =
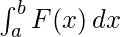
Propiedades de la Distribución Discreta:
1.= 1 2. E(x) =
3. V(x) =
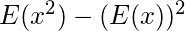
Propiedades de la Distribución Continua:
1.= 1 2. E(x) =
3. V(x) =
4. p(a < x < b) =
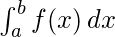
Donde,
E(x) denota el valor esperado o el valor promedio de la variable aleatoria x,
V(x) denota la varianza de la variable aleatoria x.
Tipos de distribuciones: