Análisis de datos GRE | Métodos numéricos para describir datos

Los datos se pueden describir numéricamente mediante varias estadísticas o medidas estadísticas. Estas medidas estadísticas a menudo se agrupan en 3 categorías:

1. Measures of central tendency
2. Measures of position
3. Measures of dispersion

Medidas de tendencia central:

En estadística, una tendencia central (o medida de tendencia central) es un valor central o típico para una distribución de probabilidad. También puede denominarse centro o ubicación de la distribución.
Las medidas de tendencia central indican el «centro» de los datos a lo largo de la recta numérica y generalmente se informan como valores que representan los datos. Hay tres medidas comunes de tendencia central:

Media aritmética, generalmente llamada promedio o simplemente la media
Mediana
Modo

1. Media Aritmética :
Es la conocida medida de tendencia central. La media es el promedio de un conjunto dado de datos. Para calcular la media de n números, tome la suma de los n números y divídala por n.

La media para datos no agrupados se puede definir como,

Media para datos agrupados:

Donde,
f es la frecuencia en cada clase,
x es el punto medio en cada clase,
n es el número total de puntajes

Ejemplo:
hay 16 números en una lista, encuentra la media (promedio)

 2, 4, 4, 5, 7, 7, 7, 7, 7, 7, 8, 8, 9, 9, 9, 9

Explicación:
hay 6 valores diferentes, por lo que se puede considerar como una media ponderada porque varios valores se repiten en una lista. Por lo tanto, 2 ocurren 1 vez, 4 ocurren 2 veces, 5 ocurren 1 vez, 7 ocurren 6 veces, 8 ocurren 2 veces, 9 ocurren 4 veces

Mean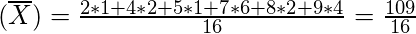

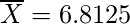
2. Mediana :
la media puede verse afectada por unos pocos valores que se encuentran muy por encima o por debajo del resto de los datos, porque estos valores contribuyen directamente a la suma de los datos y, por lo tanto, a la media. Por el contrario, la mediana es una medida de tendencia central que no se ve afectada por valores inusualmente altos o bajos en relación con el resto de los datos.

La mediana es el valor medio de un conjunto de datos. Para calcular la mediana de n números, primero ordena los números de menor a mayor.

Si n es impar, la mediana es el número del medio
Si n es par entonces la mediana es el promedio de dos valores medios

Mediana para datos agrupados:

Median =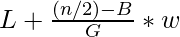

Donde,
L es el límite de clase inferior del grupo que contiene la mediana,
n es el número total de datos,
B es la frecuencia acumulada de los grupos antes del grupo mediano,
G es la frecuencia del grupo mediano,
w es el ancho del grupo

Ejemplo:
Considere 6 números, encuentre la media y la mediana, reemplace 8 con 38 y luego vuelva a encontrar la media y la mediana.

 4, 4, 5, 7, 8, 8

Explicación:
Aquí n es par, entonces

Median = avg (value at (n/2) + value at (n/2)+1)
Median = 



And,

Mean =

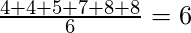
Ahora reemplazando 8 por 38, la mediana seguirá siendo la misma, es decir, 6, pero la media se verá afectada.

Mean =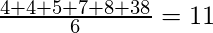

3. Moda :
La moda es el valor que ocurre con mayor frecuencia en un conjunto de observaciones. La moda de los 6 números en la lista 1, 3, 6, 4, 3, 5 es 3 porque la frecuencia de 3 es mayor que todos los demás elementos.

Ejemplo:
modo de búsqueda de cada parte

(a) 1, 2, 4, 7
(b) 1, 1, 2, 2, 3, 4

Explicación:

(a) There is no mode (mode = none)
(b) There are 2 modes in this case 1, 2 (mode = 1, 2)

Medidas de posición:

Hay tres posiciones o ubicaciones más básicas en una lista de datos numéricos ordenados de menor a mayor

El comienzo, o el valor mínimo L
El final, o el mayor valor G
El medio, o mediana M

Aparte de estas medidas más comunes de posiciones son

Cuartiles
percentiles

(a). Cuartiles:
Un cuartil es un término estadístico que describe una división de observaciones en cuatro intervalos definidos. Los cuartiles dividen los datos en cuatro grupos iguales después de ordenar los datos desde el menor valor L hasta el mayor valor G. Hay tres números de cuartiles, llamados primer cuartil, segundo cuartil y tercer cuartil, que dividen los datos en cuatro grupos aproximadamente iguales.

Los números $Q_1, Q_2,$ y $Q_3$ dividen los datos en 4 grupos aproximadamente iguales de la siguiente manera. Después de enumerar los datos en orden creciente, el primer grupo consiste en los datos de L a $Q_1$ , el segundo grupo es de $Q_1$ a $Q_2$ , el tercer grupo es de $Q_2$ a $Q_3$ y el cuarto grupo es de $Q_3$ a G.

Hay varias reglas para determinar los valores exactos de $Q_1, Q_2$ y $Q_3$ . Básicamente $Q_2$ es mediana . Para $Q_1$ y $Q_3$ ordena los datos en orden creciente:

$Q_1$ es la mediana de la primera mitad de los datos en la lista ordenada,
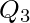$Q_3$ es la mediana de la segunda mitad de los datos en la lista ordenada,

Ejemplo:
Encuentra los cuartiles para la lista de 16 números,

2, 4, 4, 5, 7, 7, 7, 7, 7, 7, 8, 8, 9, 9, 9, 9

Explicación:

Median() = 

 = 7

Para $Q_1$ y $Q_3$ dividir los datos en dos grupos más pequeños. El primer grupo contiene 2, 4, 4, 5, 7, 7, 7, 7 y el segundo grupo contiene 7, 7, 8, 8, 9, 9, 9, 9 ahora,

 = 6 (average of 6 and 7)

 = 8.5 (average of 8 and 9)

En este ejemplo, podemos decir que 4 está en el primer cuartil (o primer grupo), 8 está en el tercer cuartil (tercer grupo) y 9 está en el cuarto cuartil. La frase “en un cuartil” se refiere a estar en uno de los cuatro grupos determinados por $Q_1, Q_2$ , y $Q_3$ .

(b). Percentiles:
los percentiles se utilizan principalmente para listas muy grandes de datos numéricos ordenados de menor a mayor. En lugar de cuatro grupos, divide los datos en 100 grupos iguales. Los percentiles 99 $P_1, P_2, P_3, P_4 ...... P_9_9$ dividen los datos en 100 grupos iguales. Aquí,

 = 

 = 

 =

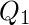
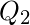
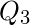
El percentil en el examen competitivo se calcula como,

Percentile = (number of people behind you / total number of people) x 100

Medidas de dispersión:

Las medidas de dispersión indican el grado de dispersión de los datos. Las estadísticas más comunes utilizadas como medidas de dispersión son,

El rango
El rango intercuartílico
La desviación estándar

1. Rango:
el rango refleja la dispersión máxima de los datos. El rango de los números en un grupo de datos es la diferencia entre el mayor número G en los datos y el menor número L en los datos; eso es,

Range(R) = G-L

A veces, un valor de datos es inusualmente pequeño o inusualmente grande en comparación con el resto de los datos. Estos datos se denominan valores atípicos . Un valor atípico es un punto de datos que difiere significativamente de otras observaciones. Los valores atípicos se encuentran tan lejos del resto de los datos. El rango se ve afectado por valores atípicos

Ejemplo:
se dan cinco números para encontrar el rango,

11, 10, 5, 13, 21

Explicación:

Greatest number (G) = 21
Least number (L) = 5
Range (R) = 21-5 = 16

2. Rango intercuartil :
El rango intercuartil se define como la diferencia entre el tercer cuartil y el primer cuartil. Es decir, $Q_3 - Q_1$ . Mide la dispersión de la mitad media de los datos y no se ve afectada por los valores atípicos.

3. Desviación estándar:
La desviación estándar es una medida de dispersión. Es una medida de cuán dispersos están los números. símbolo es $\sigma$ . Cuanto más se alejan los datos de la media, mayor es la desviación estándar; y cuanto más se agrupan los datos alrededor de la media, menor es la desviación estándar.

La desviación estándar de un grupo de datos numéricos se puede calcular como,

Calcular la media de los valores,
Encuentre la diferencia entre la media y cada uno de los valores,
Elevar al cuadrado cada una de las diferencias,
Encuentre el promedio de las diferencias al cuadrado,
Saque la raíz cuadrada no negativa del promedio de las diferencias al cuadrado,

Consulte la media, la varianza y la desviación estándar

Publicación traducida automáticamente

Artículo escrito por dheeraj01 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Medidas de tendencia central:

Medidas de posición:

Medidas de dispersión:

Deja una respuesta Cancelar la respuesta