Análisis de regresión en programación R

En estadística, la Regresión Logística es un modelo que toma variables de respuesta (variable dependiente) y características (variables independientes) para determinar la probabilidad estimada de un evento. Se usa un modelo logístico cuando la variable de respuesta tiene valores categóricos como 0 o 1. Por ejemplo, un estudiante aprobará/reprobará, un correo es spam o no, determinando las imágenes, etc. En este artículo, discutiremos la regresión análisis, tipos de regresión e implementación de regresión logística en programación R.

Análisis de regresión en R

El análisis de regresión es un grupo de procesos estadísticos que se utilizan en la programación y las estadísticas de R para determinar la relación entre las variables del conjunto de datos. Generalmente, el análisis de regresión se usa para determinar la relación entre las variables dependientes e independientes del conjunto de datos. El análisis de regresión ayuda a comprender cómo cambian las variables dependientes cuando una de las variables independientes cambia y otras variables independientes se mantienen constantes. Esto ayuda a construir un modelo de regresión y, además, ayuda a pronosticar los valores con respecto a un cambio en una de las variables independientes. Sobre la base de los tipos de variables dependientes, varias variables independientes y la forma de la línea de regresión, existen 4 tipos de técnicas de análisis de regresión, es decir, regresión lineal, regresión logística,

Tipos de análisis de regresión

Regresión lineal

La regresión lineal es una de las técnicas de regresión más utilizadas para modelar la relación entre dos variables. Utiliza una relación lineal para modelar la línea de regresión. Hay 2 variables utilizadas en la ecuación de relación lineal, es decir, variable predictora y variable de respuesta.

y = hacha + b

dónde, 

• y es la variable de respuesta
• x es la variable predictora
• a y b son los coeficientes

La línea de regresión creada usando esta técnica es una línea recta. La variable de respuesta se deriva de las variables predictoras. Las variables predictoras se estiman utilizando algunos experimentos estadísticos. La regresión lineal es ampliamente utilizada pero estas técnicas no son capaces de predecir la probabilidad.

Regresión logística

Por otro lado, la regresión logística tiene una ventaja sobre la regresión lineal ya que es capaz de predecir los valores dentro del rango. La regresión logística se utiliza para predecir los valores dentro del rango categórico. Por ejemplo, hombre o mujer, ganador o perdedor, etc.

La regresión logística utiliza la siguiente función sigmoidal:

dónde,  

• y representa la variable de respuesta
• z representa la ecuación de variables independientes o características

Regresión logística multinomial

La regresión logística multinomial es una técnica avanzada de regresión logística que toma más de 2 variables categóricas a diferencia de la regresión logística que toma 2 variables categóricas. Por ejemplo, un investigador de biología encontró un nuevo tipo de especie y el tipo de especie se puede determinar en función de muchos factores, como el tamaño, la forma, el color de los ojos, el factor ambiental de su vida, etc.

Regresión logística ordinal

La regresión logística ordinal también es una extensión de la regresión logística. Se utiliza para predecir los valores como diferentes niveles de categoría (ordenados). En palabras simples, predice el rango. Por ejemplo, un restaurante crea una encuesta sobre la calidad del sabor de la comida y, utilizando la regresión logística ordinal, se puede crear una variable de respuesta de la encuesta en una escala de cualquier intervalo, como 1-10, que ayuda a determinar la respuesta del cliente a sus alimentos.

Implementación de Regresión Logística en programación R

En lenguaje R, el modelo de regresión logística se crea utilizando la función glm(). 

Sintaxis: glm(fórmula, familia = binomial)
Parámetros:  
fórmula: representa una ecuación en base a la cual se debe ajustar el modelo. 
familia: representa el tipo de función que se utilizará, es decir, binomial para regresión logística 
 

Para conocer más parámetros opcionales de la función glm(), use el siguiente comando en R: 

help("glm")

Ejemplo: 

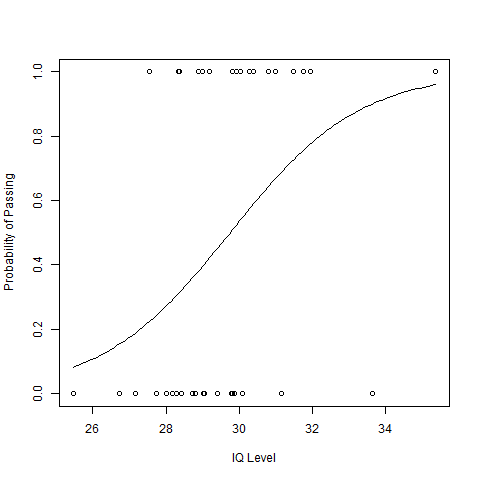
Supongamos un vector del nivel de CI de los estudiantes en una clase. Otro vector contiene el resultado del alumno correspondiente, es decir, reprobar o aprobar (0 o 1) en un examen. 

# Generate random IQ values with mean = 30 and sd =2
IQ <- rnorm(40, 30, 2)
 
# Sorting IQ level in ascending order
IQ <- sort(IQ)
 
# Generate vector with pass and fail values of 40 students
result <- c(0, 0, 0, 1, 0, 0, 0, 0, 0, 1,
1, 0, 0, 0, 1, 1, 0, 0, 1, 0,
0, 0, 1, 0, 0, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 1, 1, 0, 1)
 
# Data Frame
df <- as.data.frame(cbind(IQ, result))
 
# Print data frame
print(df)
 
# output to be present as PNG file
png(file="LogisticRegressionGFG.png")
 
# Plotting IQ on x-axis and result on y-axis
plot(IQ, result, xlab = "IQ Level",
ylab = "Probability of Passing")
 
# Create a logistic model
g = glm(result~IQ, family=binomial, df)
 
# Create a curve based on prediction using the regression model
curve(predict(g, data.frame(IQ=x), type="resp"), add=TRUE)
 
# This Draws a set of points
# Based on fit to the regression model
points(IQ, fitted(g), pch=30)
 
# Summary of the regression model
summary(g)
 
# saving the file
dev.off()

Producción: 

         IQ result
1  25.46872      0
2  26.72004      0
3  27.16163      0
4  27.55291      1
5  27.72577      0
6  28.00731      0
7  28.18095      0
8  28.28053      0
9  28.29086      0
10 28.34474      1
11 28.35581      1
12 28.40969      0
13 28.72583      0
14 28.81105      0
15 28.87337      1
16 29.00383      1
17 29.01762      0
18 29.03629      0
19 29.18109      1
20 29.39251      0
21 29.40852      0
22 29.78844      0
23 29.80456      1
24 29.81815      0
25 29.86478      0
26 29.91535      1
27 30.04204      1
28 30.09565      0
29 30.28495      1
30 30.39359      1
31 30.78886      1
32 30.79307      1
33 30.98601      1
34 31.14602      0
35 31.48225      1
36 31.74983      1
37 31.94705      1
38 31.94772      1
39 33.63058      0
40 35.35096      1

Call:
glm(formula = result ~ IQ, family = binomial, data = df)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.1451  -0.9742  -0.4950   1.0326   1.7283  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept) -16.8093     7.3368  -2.291   0.0220 *
IQ            0.5651     0.2482   2.276   0.0228 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 55.352  on 39  degrees of freedom
Residual deviance: 48.157  on 38  degrees of freedom
AIC: 52.157

Number of Fisher Scoring iterations: 4