Dados los valores de dos Nodes en un árbol binario, encuentre el antepasado común más bajo ( LCA ). Se puede suponer que ambos Nodes existen en el árbol.
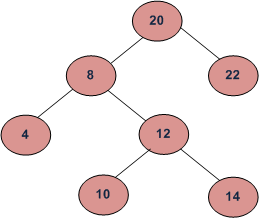
Por ejemplo, considere el árbol binario en el diagrama, LCA de 10 y 14 es 12 y LCA de 8 y 14 es 8.
Sea T un árbol con raíz. El ancestro común más bajo entre dos Nodes n1 y n2 se define como el Node más bajo en T que tiene tanto n1 como n2 como descendientes (donde permitimos que un Node sea descendiente de sí mismo). Fuente: Wikipedia .
Hemos discutido diferentes enfoques para encontrar LCA en el conjunto 1 . Encontrar LCA se vuelve fácil cuando se proporciona un puntero principal, ya que podemos encontrar fácilmente todos los ancestros de un Node usando un puntero principal.
A continuación se muestran los pasos para encontrar LCA.
- Cree una tabla hash vacía.
- Inserte n1 y todos sus ancestros en la tabla hash.
- Verifique si n2 o cualquiera de sus ancestros existe en la tabla hash, en caso afirmativo, devuelva el primer ancestro existente.
A continuación se muestra la implementación de los pasos anteriores.
C
// C++ program to find lowest common ancestor using parent pointer
#include <bits/stdc++.h>
using namespace std;
// A Tree Node
struct Node
{
Node *left, *right, *parent;
int key;
};
// A utility function to create a new BST node
Node *newNode(int item)
{
Node *temp = new Node;
temp->key = item;
temp->parent = temp->left = temp->right = NULL;
return temp;
}
/* A utility function to insert a new node with
given key in Binary Search Tree */
Node *insert(Node *node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
{
node->left = insert(node->left, key);
node->left->parent = node;
}
else if (key > node->key)
{
node->right = insert(node->right, key);
node->right->parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// To find LCA of nodes n1 and n2 in Binary Tree
Node *LCA(Node *n1, Node *n2)
{
// Creata a map to store ancestors of n1
map <Node *, bool> ancestors;
// Insert n1 and all its ancestors in map
while (n1 != NULL)
{
ancestors[n1] = true;
n1 = n1->parent;
}
// Check if n2 or any of its ancestors is in
// map.
while (n2 != NULL)
{
if (ancestors.find(n2) != ancestors.end())
return n2;
n2 = n2->parent;
}
return NULL;
}
// Driver method to test above functions
int main(void)
{
Node * root = NULL;
root = insert(root, 20);
root = insert(root, 8);
root = insert(root, 22);
root = insert(root, 4);
root = insert(root, 12);
root = insert(root, 10);
root = insert(root, 14);
Node *n1 = root->left->right->left;
Node *n2 = root->left;
Node *lca = LCA(n1, n2);
printf("LCA of %d and %d is %d \n", n1->key, n2->key, lca->key);
return 0;
}
Java
import java.util.HashMap;
import java.util.Map;
// Java program to find lowest common ancestor using parent pointer
// A tree node
class Node
{
int key;
Node left, right, parent;
Node(int key)
{
this.key = key;
left = right = parent = null;
}
}
class BinaryTree
{
Node root, n1, n2, lca;
/* A utility function to insert a new node with
given key in Binary Search Tree */
Node insert(Node node, int key)
{
/* If the tree is empty, return a new node */
if (node == null)
return new Node(key);
/* Otherwise, recur down the tree */
if (key < node.key)
{
node.left = insert(node.left, key);
node.left.parent = node;
}
else if (key > node.key)
{
node.right = insert(node.right, key);
node.right.parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// To find LCA of nodes n1 and n2 in Binary Tree
Node LCA(Node n1, Node n2)
{
// Creata a map to store ancestors of n1
Map<Node, Boolean> ancestors = new HashMap<Node, Boolean>();
// Insert n1 and all its ancestors in map
while (n1 != null)
{
ancestors.put(n1, Boolean.TRUE);
n1 = n1.parent;
}
// Check if n2 or any of its ancestors is in
// map.
while (n2 != null)
{
if (ancestors.containsKey(n2) != ancestors.isEmpty())
return n2;
n2 = n2.parent;
}
return null;
}
// Driver method to test above functions
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 8);
tree.root = tree.insert(tree.root, 22);
tree.root = tree.insert(tree.root, 4);
tree.root = tree.insert(tree.root, 12);
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 14);
tree.n1 = tree.root.left.right.left;
tree.n2 = tree.root.left;
tree.lca = tree.LCA(tree.n1, tree.n2);
System.out.println("LCA of " + tree.n1.key + " and " + tree.n2.key
+ " is " + tree.lca.key);
}
}
// This code has been contributed by Mayank Jaiswal(mayank_24)
C#
// C# program to find lowest common ancestor using parent pointer
// A tree node
using System;
using System.Collections;
using System.Collections.Generic;
public class Node
{
public int key;
public Node left, right, parent;
public Node(int key)
{
this.key = key;
left = right = parent = null;
}
}
class BinaryTree
{
Node root, n1, n2, lca;
/* A utility function to insert a new node with
given key in Binary Search Tree */
Node insert(Node node, int key)
{
/* If the tree is empty, return a new node */
if (node == null)
return new Node(key);
/* Otherwise, recur down the tree */
if (key < node.key)
{
node.left = insert(node.left, key);
node.left.parent = node;
}
else if (key > node.key)
{
node.right = insert(node.right, key);
node.right.parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// To find LCA of nodes n1 and n2 in Binary Tree
Node LCA(Node n1, Node n2)
{
// Creata a map to store ancestors of n1
Dictionary<Node, Boolean> ancestors = new Dictionary<Node, Boolean>();
// Insert n1 and all its ancestors in map
while (n1 != null)
{
ancestors.Add(n1,true);
n1 = n1.parent;
}
// Check if n2 or any of its ancestors is in
// map.
while (n2 != null)
{
if (ancestors.ContainsKey(n2))
return n2;
n2 = n2.parent;
}
return null;
}
// Driver code
public static void Main(String []args)
{
BinaryTree tree = new BinaryTree();
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 8);
tree.root = tree.insert(tree.root, 22);
tree.root = tree.insert(tree.root, 4);
tree.root = tree.insert(tree.root, 12);
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 14);
tree.n1 = tree.root.left.right.left;
tree.n2 = tree.root.left;
tree.lca = tree.LCA(tree.n1, tree.n2);
Console.WriteLine("LCA of " + tree.n1.key + " and " + tree.n2.key
+ " is " + tree.lca.key);
}
}
// This code is contributed by Arnab Kundu
Producción:
LCA of 10 and 8 is 8
Nota: la implementación anterior utiliza la inserción del árbol de búsqueda binaria para crear un árbol binario, pero la función LCA es para cualquier árbol binario (no necesariamente un árbol de búsqueda binaria).
Complejidad de tiempo: O (h) donde h es la altura del árbol binario si usamos una tabla hash para implementar la solución (tenga en cuenta que la solución anterior usa un mapa que toma O (Log h) tiempo para insertar y encontrar). Entonces, la complejidad de tiempo de la implementación anterior es O (h Log h).
Espacio Auxiliar : O(h)
AO(h) tiempo y O(1) Solución de espacio adicional :
la solución anterior requiere espacio adicional porque necesitamos usar una tabla hash para almacenar los ancestros visitados. Podemos resolver el problema en el espacio adicional O(1) usando el siguiente hecho: si ambos Nodes están al mismo nivel y si cruzamos hacia arriba usando punteros principales de ambos Nodes, el primer Node común en la ruta a la raíz es lca.
La idea es encontrar las profundidades de los Nodes dados y mover hacia arriba el puntero del Node más profundo por la diferencia entre las profundidades. Una vez que ambos Nodes alcancen el mismo nivel, atraviéselos hacia arriba y devuelva el primer Node común.
Gracias a Mysterious Mind por sugerir este enfoque.
C++
// C++ program to find lowest common ancestor using parent pointer
#include <bits/stdc++.h>
using namespace std;
// A Tree Node
struct Node
{
Node *left, *right, *parent;
int key;
};
// A utility function to create a new BST node
Node *newNode(int item)
{
Node *temp = new Node;
temp->key = item;
temp->parent = temp->left = temp->right = NULL;
return temp;
}
/* A utility function to insert a new node with
given key in Binary Search Tree */
Node *insert(Node *node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
{
node->left = insert(node->left, key);
node->left->parent = node;
}
else if (key > node->key)
{
node->right = insert(node->right, key);
node->right->parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// A utility function to find depth of a node
// (distance of it from root)
int depth(Node *node)
{
int d = -1;
while (node)
{
++d;
node = node->parent;
}
return d;
}
// To find LCA of nodes n1 and n2 in Binary Tree
Node *LCA(Node *n1, Node *n2)
{
// Find depths of two nodes and differences
int d1 = depth(n1), d2 = depth(n2);
int diff = d1 - d2;
// If n2 is deeper, swap n1 and n2
if (diff < 0)
{
Node * temp = n1;
n1 = n2;
n2 = temp;
diff = -diff;
}
// Move n1 up until it reaches the same level as n2
while (diff--)
n1 = n1->parent;
// Now n1 and n2 are at same levels
while (n1 && n2)
{
if (n1 == n2)
return n1;
n1 = n1->parent;
n2 = n2->parent;
}
return NULL;
}
// Driver method to test above functions
int main(void)
{
Node * root = NULL;
root = insert(root, 20);
root = insert(root, 8);
root = insert(root, 22);
root = insert(root, 4);
root = insert(root, 12);
root = insert(root, 10);
root = insert(root, 14);
Node *n1 = root->left->right->left;
Node *n2 = root->right;
Node *lca = LCA(n1, n2);
printf("LCA of %d and %d is %d \n", n1->key, n2->key, lca->key);
return 0;
}
Java
import java.util.HashMap;
import java.util.Map;
// Java program to find lowest common ancestor using parent pointer
// A tree node
class Node
{
int key;
Node left, right, parent;
Node(int key)
{
this.key = key;
left = right = parent = null;
}
}
class BinaryTree
{
Node root, n1, n2, lca;
/* A utility function to insert a new node with
given key in Binary Search Tree */
Node insert(Node node, int key)
{
/* If the tree is empty, return a new node */
if (node == null)
return new Node(key);
/* Otherwise, recur down the tree */
if (key < node.key)
{
node.left = insert(node.left, key);
node.left.parent = node;
}
else if (key > node.key)
{
node.right = insert(node.right, key);
node.right.parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// A utility function to find depth of a node
// (distance of it from root)
int depth(Node node)
{
int d = -1;
while (node != null)
{
++d;
node = node.parent;
}
return d;
}
// To find LCA of nodes n1 and n2 in Binary Tree
Node LCA(Node n1, Node n2)
{
// Find depths of two nodes and differences
int d1 = depth(n1), d2 = depth(n2);
int diff = d1 - d2;
// If n2 is deeper, swap n1 and n2
if (diff < 0)
{
Node temp = n1;
n1 = n2;
n2 = temp;
diff = -diff;
}
// Move n1 up until it reaches the same level as n2
while (diff-- != 0)
n1 = n1.parent;
// Now n1 and n2 are at same levels
while (n1 != null && n2 != null)
{
if (n1 == n2)
return n1;
n1 = n1.parent;
n2 = n2.parent;
}
return null;
}
// Driver method to test above functions
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 8);
tree.root = tree.insert(tree.root, 22);
tree.root = tree.insert(tree.root, 4);
tree.root = tree.insert(tree.root, 12);
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 14);
tree.n1 = tree.root.left.right.left;
tree.n2 = tree.root.right;
tree.lca = tree.LCA(tree.n1, tree.n2);
System.out.println("LCA of " + tree.n1.key + " and " + tree.n2.key
+ " is " + tree.lca.key);
}
}
// This code has been contributed by Mayank Jaiswal(mayank_24)
C#
// C# program to find lowest common
// ancestor using parent pointer
using System;
// A tree node
public class Node
{
public int key;
public Node left, right, parent;
public Node(int key)
{
this.key = key;
left = right = parent = null;
}
}
class GFG
{
public Node root, n1, n2, lca;
/* A utility function to insert a new
node with given key in Binary Search Tree */
public virtual Node insert(Node node, int key)
{
/* If the tree is empty, return
a new node */
if (node == null)
{
return new Node(key);
}
/* Otherwise, recur down the tree */
if (key < node.key)
{
node.left = insert(node.left, key);
node.left.parent = node;
}
else if (key > node.key)
{
node.right = insert(node.right, key);
node.right.parent = node;
}
/* return the (unchanged) node pointer */
return node;
}
// A utility function to find depth of a
// node (distance of it from root)
public virtual int depth(Node node)
{
int d = -1;
while (node != null)
{
++d;
node = node.parent;
}
return d;
}
// To find LCA of nodes n1 and n2
// in Binary Tree
public virtual Node LCA(Node n1, Node n2)
{
// Find depths of two nodes
// and differences
int d1 = depth(n1), d2 = depth(n2);
int diff = d1 - d2;
// If n2 is deeper, swap n1 and n2
if (diff < 0)
{
Node temp = n1;
n1 = n2;
n2 = temp;
diff = -diff;
}
// Move n1 up until it reaches
// the same level as n2
while (diff-- != 0)
{
n1 = n1.parent;
}
// Now n1 and n2 are at same levels
while (n1 != null && n2 != null)
{
if (n1 == n2)
{
return n1;
}
n1 = n1.parent;
n2 = n2.parent;
}
return null;
}
// Driver Code
public static void Main(string[] args)
{
GFG tree = new GFG();
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 8);
tree.root = tree.insert(tree.root, 22);
tree.root = tree.insert(tree.root, 4);
tree.root = tree.insert(tree.root, 12);
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 14);
tree.n1 = tree.root.left.right.left;
tree.n2 = tree.root.right;
tree.lca = tree.LCA(tree.n1, tree.n2);
Console.WriteLine("LCA of " + tree.n1.key +
" and " + tree.n2.key +
" is " + tree.lca.key);
}
}
// This code is contributed by Shrikant13
Producción :
LCA of 10 and 22 is 20
Es posible que desee ver los siguientes artículos también:
antepasado común más bajo en un árbol binario | Serie 1
Ancestro común más bajo en un árbol de búsqueda binario.
Encuentre LCA en árbol binario usando RMQ
Este artículo es una contribución de Dheeraj Gupta . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA