¿Qué es el ancestro común más bajo en el árbol binario?
El ancestro común más bajo es el Node más bajo en el árbol que tiene n1 y n2 como descendientes, donde n1 y n2 son los Nodes para los que deseamos encontrar el LCA. Por lo tanto, el LCA de un árbol binario con Nodes n1 y n2 es el ancestro compartido de n1 y n2 que se encuentra más alejado de la raíz.
Aplicación del ancestro común más bajo (LCA):
para determinar la distancia entre pares de Nodes en un árbol: la distancia de n1 a n2 se puede calcular como la distancia de la raíz a n1, más la distancia de la raíz a n2, menos el doble de la distancia desde la raíz hasta su ancestro común más bajo.
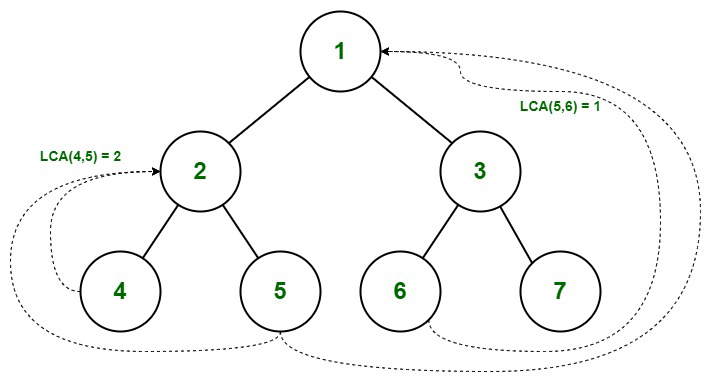
Ancestro común más bajo en el árbol binario
Enfoque 1 (Al almacenar rutas de raíz a n1 y de raíz a n2):
La idea de este enfoque es almacenar la ruta desde la raíz a n1 y desde la raíz a n2 en dos estructuras de datos separadas. Luego mire simultáneamente los valores almacenados en la estructura de datos y busque la primera falta de coincidencia.
Ilustración:

Encuentre el LCA de 5 y 6
Camino desde la raíz a 5 = { 1, 2, 5 }
Camino desde la raíz a 6 = { 1, 3, 6 }
- Empezamos a comprobar desde el índice 0. Como ambos valores coinciden (pathA[0] = pathB[0]), pasamos al siguiente índice.
- pathA[1] no es igual a pathB[1], hay una discrepancia, por lo que consideramos el valor anterior.
- Por lo tanto el LCA de (5,6) = 1
El siguiente es un algoritmo O(n) simple para encontrar el LCA de n1 y n2.
- Encuentre una ruta desde la raíz hasta n1 y guárdela en un vector o array.
- Encuentre una ruta desde la raíz hasta n2 y guárdela en otro vector o array.
- Recorra ambos caminos hasta que los valores en las arrays sean los mismos. Devuelve el elemento común justo antes del desajuste.
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ Program for Lowest Common Ancestor in a Binary Tree
// A O(n) solution to find LCA of two given values n1 and n2
#include <iostream>
#include <vector>
using namespace std;
// A Binary Tree node
struct Node
{
int key;
struct Node *left, *right;
};
// Utility function creates a new binary tree node with given key
Node * newNode(int k)
{
Node *temp = new Node;
temp->key = k;
temp->left = temp->right = NULL;
return temp;
}
// Finds the path from root node to given root of the tree, Stores the
// path in a vector path[], returns true if path exists otherwise false
bool findPath(Node *root, vector<int> &path, int k)
{
// base case
if (root == NULL) return false;
// Store this node in path vector. The node will be removed if
// not in path from root to k
path.push_back(root->key);
// See if the k is same as root's key
if (root->key == k)
return true;
// Check if k is found in left or right sub-tree
if ( (root->left && findPath(root->left, path, k)) ||
(root->right && findPath(root->right, path, k)) )
return true;
// If not present in subtree rooted with root, remove root from
// path[] and return false
path.pop_back();
return false;
}
// Returns LCA if node n1, n2 are present in the given binary tree,
// otherwise return -1
int findLCA(Node *root, int n1, int n2)
{
// to store paths to n1 and n2 from the root
vector<int> path1, path2;
// Find paths from root to n1 and root to n2. If either n1 or n2
// is not present, return -1
if ( !findPath(root, path1, n1) || !findPath(root, path2, n2))
return -1;
/* Compare the paths to get the first different value */
int i;
for (i = 0; i < path1.size() && i < path2.size() ; i++)
if (path1[i] != path2[i])
break;
return path1[i-1];
}
// Driver program to test above functions
int main()
{
// Let us create the Binary Tree shown in above diagram.
Node * root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
cout << "LCA(4, 5) = " << findLCA(root, 4, 5);
cout << "\nLCA(4, 6) = " << findLCA(root, 4, 6);
cout << "\nLCA(3, 4) = " << findLCA(root, 3, 4);
cout << "\nLCA(2, 4) = " << findLCA(root, 2, 4);
return 0;
}
Java
// Java Program for Lowest Common Ancestor in a Binary Tree
// A O(n) solution to find LCA of two given values n1 and n2
import java.util.ArrayList;
import java.util.List;
// A Binary Tree node
class Node {
int data;
Node left, right;
Node(int value) {
data = value;
left = right = null;
}
}
public class BT_NoParentPtr_Solution1
{
Node root;
private List<Integer> path1 = new ArrayList<>();
private List<Integer> path2 = new ArrayList<>();
// Finds the path from root node to given root of the tree.
int findLCA(int n1, int n2) {
path1.clear();
path2.clear();
return findLCAInternal(root, n1, n2);
}
private int findLCAInternal(Node root, int n1, int n2) {
if (!findPath(root, n1, path1) || !findPath(root, n2, path2)) {
System.out.println((path1.size() > 0) ? "n1 is present" : "n1 is missing");
System.out.println((path2.size() > 0) ? "n2 is present" : "n2 is missing");
return -1;
}
int i;
for (i = 0; i < path1.size() && i < path2.size(); i++) {
// System.out.println(path1.get(i) + " " + path2.get(i));
if (!path1.get(i).equals(path2.get(i)))
break;
}
return path1.get(i-1);
}
// Finds the path from root node to given root of the tree, Stores the
// path in a vector path[], returns true if path exists otherwise false
private boolean findPath(Node root, int n, List<Integer> path)
{
// base case
if (root == null) {
return false;
}
// Store this node . The node will be removed if
// not in path from root to n.
path.add(root.data);
if (root.data == n) {
return true;
}
if (root.left != null && findPath(root.left, n, path)) {
return true;
}
if (root.right != null && findPath(root.right, n, path)) {
return true;
}
// If not present in subtree rooted with root, remove root from
// path[] and return false
path.remove(path.size()-1);
return false;
}
// Driver code
public static void main(String[] args)
{
BT_NoParentPtr_Solution1 tree = new BT_NoParentPtr_Solution1();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
System.out.println("LCA(4, 5): " + tree.findLCA(4,5));
System.out.println("LCA(4, 6): " + tree.findLCA(4,6));
System.out.println("LCA(3, 4): " + tree.findLCA(3,4));
System.out.println("LCA(2, 4): " + tree.findLCA(2,4));
}
}
// This code is contributed by Sreenivasulu Rayanki.
Python3
# Python Program for Lowest Common Ancestor in a Binary Tree
# O(n) solution to find LCS of two given values n1 and n2
# A binary tree node
class Node:
# Constructor to create a new binary node
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Finds the path from root node to given root of the tree.
# Stores the path in a list path[], returns true if path
# exists otherwise false
def findPath( root, path, k):
# Baes Case
if root is None:
return False
# Store this node is path vector. The node will be
# removed if not in path from root to k
path.append(root.key)
# See if the k is same as root's key
if root.key == k :
return True
# Check if k is found in left or right sub-tree
if ((root.left != None and findPath(root.left, path, k)) or
(root.right!= None and findPath(root.right, path, k))):
return True
# If not present in subtree rooted with root, remove
# root from path and return False
path.pop()
return False
# Returns LCA if node n1 , n2 are present in the given
# binary tree otherwise return -1
def findLCA(root, n1, n2):
# To store paths to n1 and n2 fromthe root
path1 = []
path2 = []
# Find paths from root to n1 and root to n2.
# If either n1 or n2 is not present , return -1
if (not findPath(root, path1, n1) or not findPath(root, path2, n2)):
return -1
# Compare the paths to get the first different value
i = 0
while(i < len(path1) and i < len(path2)):
if path1[i] != path2[i]:
break
i += 1
return path1[i-1]
# Driver program to test above function
# Let's create the Binary Tree shown in above diagram
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print ("LCA(4, 5) = %d" %(findLCA(root, 4, 5,)))
print ("LCA(4, 6) = %d" %(findLCA(root, 4, 6)))
print ("LCA(3, 4) = %d" %(findLCA(root,3,4)))
print ("LCA(2, 4) = %d" %(findLCA(root,2, 4)))
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// C# Program for Lowest Common
// Ancestor in a Binary Tree
// A O(n) solution to find LCA
// of two given values n1 and n2
using System.Collections;
using System;
// A Binary Tree node
class Node
{
public int data;
public Node left, right;
public Node(int value)
{
data = value;
left = right = null;
}
}
public class BT_NoParentPtr_Solution1
{
Node root;
private ArrayList path1 =
new ArrayList();
private ArrayList path2 =
new ArrayList();
// Finds the path from root
// node to given root of the
// tree.
int findLCA(int n1,
int n2)
{
path1.Clear();
path2.Clear();
return findLCAInternal(root,
n1, n2);
}
private int findLCAInternal(Node root,
int n1, int n2)
{
if (!findPath(root, n1, path1) ||
!findPath(root, n2, path2)) {
Console.Write((path1.Count > 0) ?
"n1 is present" :
"n1 is missing");
Console.Write((path2.Count > 0) ?
"n2 is present" :
"n2 is missing");
return -1;
}
int i;
for (i = 0; i < path1.Count &&
i < path2.Count; i++)
{
// System.out.println(path1.get(i)
// + " " + path2.get(i));
if ((int)path1[i] !=
(int)path2[i])
break;
}
return (int)path1[i - 1];
}
// Finds the path from root node
// to given root of the tree,
// Stores the path in a vector
// path[], returns true if path
// exists otherwise false
private bool findPath(Node root,
int n,
ArrayList path)
{
// base case
if (root == null)
{
return false;
}
// Store this node . The node
// will be removed if not in
// path from root to n.
path.Add(root.data);
if (root.data == n)
{
return true;
}
if (root.left != null &&
findPath(root.left,
n, path))
{
return true;
}
if (root.right != null &&
findPath(root.right,
n, path))
{
return true;
}
// If not present in subtree
//rooted with root, remove root
// from path[] and return false
path.RemoveAt(path.Count - 1);
return false;
}
// Driver code
public static void Main(String[] args)
{
BT_NoParentPtr_Solution1 tree =
new BT_NoParentPtr_Solution1();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Console.Write("LCA(4, 5): " +
tree.findLCA(4, 5));
Console.Write("\nLCA(4, 6): " +
tree.findLCA(4, 6));
Console.Write("\nLCA(3, 4): " +
tree.findLCA(3, 4));
Console.Write("\nLCA(2, 4): " +
tree.findLCA(2, 4));
}
}
// This code is contributed by Rutvik_56
Javascript
<script>
// JavaScript Program for Lowest Common
// Ancestor in a Binary Tree
// A O(n) solution to find LCA of
// two given values n1 and n2
class Node
{
constructor(value) {
this.left = null;
this.right = null;
this.data = value;
}
}
let root;
let path1 = [];
let path2 = [];
// Finds the path from root node to given root of the tree.
function findLCA(n1, n2) {
path1 = [];
path2 = [];
return findLCAInternal(root, n1, n2);
}
function findLCAInternal(root, n1, n2) {
if (!findPath(root, n1, path1) || !findPath(root, n2, path2))
{
document.write((path1.length > 0) ?
"n1 is present" : "n1 is missing");
document.write((path2.length > 0) ?
"n2 is present" : "n2 is missing");
return -1;
}
let i;
for (i = 0; i < path1.length && i < path2.length; i++) {
// System.out.println(path1.get(i) + " " + path2.get(i));
if (path1[i] != path2[i])
break;
}
return path1[i-1];
}
// Finds the path from root node to
// given root of the tree, Stores the
// path in a vector path[], returns true
// if path exists otherwise false
function findPath(root, n, path)
{
// base case
if (root == null) {
return false;
}
// Store this node . The node will be removed if
// not in path from root to n.
path.push(root.data);
if (root.data == n) {
return true;
}
if (root.left != null && findPath(root.left, n, path)) {
return true;
}
if (root.right != null && findPath(root.right, n, path)) {
return true;
}
// If not present in subtree rooted with root,
// remove root from
// path[] and return false
path.pop();
return false;
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
document.write("LCA(4, 5) = " + findLCA(4,5) + "</br>");
document.write("LCA(4, 6) = " + findLCA(4,6) + "</br>");
document.write("LCA(3, 4) = " + findLCA(3,4) + "</br>");
document.write("LCA(2, 4) = " + findLCA(2,4));
</script>
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2
Complejidad temporal: O(n). El árbol se recorre dos veces y luego se comparan las arrays de rutas.
Espacio Auxiliar: O(n). Espacio adicional para path1 y path2.
Método 2 (utilizando recorrido único):
el método 1 encuentra LCA en tiempo O(n), pero requiere tres recorridos de árbol más espacios adicionales para arrays de ruta. Si asumimos que las claves n1 y n2 están presentes en el árbol binario, podemos encontrar LCA utilizando un solo recorrido del árbol binario y sin almacenamiento adicional para arrays de ruta.
La idea es recorrer el árbol partiendo de la raíz. Si alguna de las claves proporcionadas (n1 y n2) coincide con la raíz, entonces la raíz es LCA (suponiendo que ambas claves estén presentes). Si la raíz no coincide con ninguna de las claves, recurrimos para el subárbol izquierdo y derecho. El Node que tiene una clave presente en su subárbol izquierdo y la otra clave presente en el subárbol derecho es el LCA. Si ambas claves se encuentran en el subárbol izquierdo, entonces el subárbol izquierdo también tiene LCA; de lo contrario, LCA se encuentra en el subárbol derecho.
Ilustración:

Encuentre el LCA de 5 y 6
Root apunta al Node con valor 1, ya que su valor no coincide con { 5, 6 }. Buscamos la clave en subárbol izquierdo y subárbol derecho.
- Subárbol izquierdo:
- New Root = { 2 } ≠ 5 o 6, por lo que continuaremos con nuestra recursividad
- New Root = { 4 } , su subárbol izquierdo y derecho es nulo, devolveremos NULL para esta llamada
- New Root = { 5 } , el valor coincide con 5, por lo que devolverá el Node con valor 5
- La llamada de función para root con valor 2 devolverá un valor de 5
- Subárbol derecho:
- Raíz = { 3 } ≠ 5 o 6, por lo tanto, continuamos nuestra recursividad
- Root = { 6 } = 5 o 6 , devolveremos este Node con valor 6
- Root = { 7 } ≠ 5 o 6, devolveremos NULL
- Entonces, la llamada de función para root con valor 3 devolverá el Node con valor 6
- Como tanto el subárbol izquierdo como el subárbol derecho del Node con valor 1 no son NULL, entonces 1 es el LCA
El siguiente es el algoritmo optimizado para encontrar el LCA de n1 y n2.
- Pasamos la raíz a una función auxiliar y verificamos si el valor de la raíz coincide con cualquiera de n1 y n2.
- En caso afirmativo, devuelva la raíz
- otra llamada recursiva en el subárbol izquierdo y derecho
- Básicamente, hacemos un recorrido de pedido previo, al principio verificamos si el valor raíz-> coincide con n1 o n2. Luego atraviese el subárbol izquierdo y derecho.
- Si hay alguna raíz que devuelve un valor NULL y otro NON-NULL, devolveremos el valor NON-NULL correspondiente a ese Node.
- El Node que devuelve ambos valores NON-NULL para el subárbol izquierdo y derecho es nuestro antepasado común más bajo.
C++
/* C++ Program to find LCA of n1 and n2 using one traversal of Binary Tree */
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node
{
struct Node *left, *right;
int key;
};
// Utility function to create a new tree Node
Node* newNode(int key)
{
Node *temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return temp;
}
// This function returns pointer to LCA of two given values n1 and n2.
// This function assumes that n1 and n2 are present in Binary Tree
struct Node *findLCA(struct Node* root, int n1, int n2)
{
// Base case
if (root == NULL) return NULL;
// If either n1 or n2 matches with root's key, report
// the presence by returning root (Note that if a key is
// ancestor of other, then the ancestor key becomes LCA
if (root->key == n1 || root->key == n2)
return root;
// Look for keys in left and right subtrees
Node *left_lca = findLCA(root->left, n1, n2);
Node *right_lca = findLCA(root->right, n1, n2);
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca && right_lca) return root;
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != NULL)? left_lca: right_lca;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree given in the above example
Node * root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
cout << "LCA(4, 5) = " << findLCA(root, 4, 5)->key;
cout << "\nLCA(4, 6) = " << findLCA(root, 4, 6)->key;
cout << "\nLCA(3, 4) = " << findLCA(root, 3, 4)->key;
cout << "\nLCA(2, 4) = " << findLCA(root, 2, 4)->key;
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C Program to find LCA of n1 and n2 using one traversalof
// Binary Tree
#include <stdio.h>
#include <stdlib.h>
// A Binary Tree Node
typedef struct Node {
struct Node *left, *right;
int key;
}Node;
// Utility function to create a new tree Node
Node* newNode(int key)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->key = key;
temp->left = temp->right = NULL;
return temp;
}
// This function returns pointer to LCA of two given values
// n1 and n2. This function assumes that n1 and n2 are
// present in Binary Tree
Node* findLCA(Node* root, int n1, int n2)
{
// Base case
if (root == NULL)
return NULL;
// If either n1 or n2 matches with root's key, report
// the presence by returning root (Note that if a key is
// ancestor of other, then the ancestor key becomes LCA
if (root->key == n1 || root->key == n2)
return root;
// Look for keys in left and right subtrees
Node* left_lca = findLCA(root->left, n1, n2);
Node* right_lca = findLCA(root->right, n1, n2);
// If both of the above calls return Non-NULL, then one
// key is present in once subtree and other is present
// in other, So this node is the LCA
if (left_lca && right_lca)
return root;
// Otherwise check if left subtree or right subtree is
// LCA
return (left_lca != NULL) ? left_lca : right_lca;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree given in the above example
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
printf("LCA(4, 5) = %d", findLCA(root, 4, 5)->key);
printf("\nLCA(4, 6) = %d", findLCA(root, 4, 6)->key);
printf("\nLCA(3, 4) = %d", findLCA(root, 3, 4)->key);
printf("\nLCA(2, 4) = %d", findLCA(root, 2, 4)->key);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
//Java implementation to find lowest common ancestor of
// n1 and n2 using one traversal of binary tree
/* Class containing left and right child of current
node and key value*/
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
//Root of the Binary Tree
Node root;
Node findLCA(int n1, int n2)
{
return findLCA(root, n1, n2);
}
// This function returns pointer to LCA of two given
// values n1 and n2. This function assumes that n1 and
// n2 are present in Binary Tree
Node findLCA(Node node, int n1, int n2)
{
// Base case
if (node == null)
return null;
// If either n1 or n2 matches with root's key, report
// the presence by returning root (Note that if a key is
// ancestor of other, then the ancestor key becomes LCA
if (node.data == n1 || node.data == n2)
return node;
// Look for keys in left and right subtrees
Node left_lca = findLCA(node.left, n1, n2);
Node right_lca = findLCA(node.right, n1, n2);
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca!=null && right_lca!=null)
return node;
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != null) ? left_lca : right_lca;
}
/* Driver program to test above functions */
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
System.out.println("LCA(4, 5) = " +
tree.findLCA(4, 5).data);
System.out.println("LCA(4, 6) = " +
tree.findLCA(4, 6).data);
System.out.println("LCA(3, 4) = " +
tree.findLCA(3, 4).data);
System.out.println("LCA(2, 4) = " +
tree.findLCA(2, 4).data);
}
}
Python3
# Python program to find LCA of n1 and n2 using one
# traversal of Binary tree
# A binary tree node
class Node:
# Constructor to create a new tree node
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# This function returns pointer to LCA of two given
# values n1 and n2
# This function assumes that n1 and n2 are present in
# Binary Tree
def findLCA(root, n1, n2):
# Base Case
if root is None:
return None
# If either n1 or n2 matches with root's key, report
# the presence by returning root (Note that if a key is
# ancestor of other, then the ancestor key becomes LCA
if root.key == n1 or root.key == n2:
return root
# Look for keys in left and right subtrees
left_lca = findLCA(root.left, n1, n2)
right_lca = findLCA(root.right, n1, n2)
# If both of the above calls return Non-NULL, then one key
# is present in once subtree and other is present in other,
# So this node is the LCA
if left_lca and right_lca:
return root
# Otherwise check if left subtree or right subtree is LCA
return left_lca if left_lca is not None else right_lca
# Driver program to test above function
# Let us create a binary tree given in the above example
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print ("LCA(4,5) = ", findLCA(root, 4, 5).key)
print ("LCA(4,6) = ", findLCA(root, 4, 6).key)
print ("LCA(3,4) = ", findLCA(root, 3, 4).key)
print ("LCA(2,4) = ", findLCA(root, 2, 4).key)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// C# implementation to find lowest common
// ancestor of n1 and n2 using one traversal
// of binary tree
using System;
// Class containing left and right
// child of current node and key value
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree{
// Root of the Binary Tree
Node root;
Node findLCA(int n1, int n2)
{
return findLCA(root, n1, n2);
}
// This function returns pointer to LCA
// of two given values n1 and n2. This
// function assumes that n1 and n2 are
// present in Binary Tree
Node findLCA(Node node, int n1, int n2)
{
// Base case
if (node == null)
return null;
// If either n1 or n2 matches with
// root's key, report the presence
// by returning root (Note that if
// a key is ancestor of other,
// then the ancestor key becomes LCA
if (node.data == n1 || node.data == n2)
return node;
// Look for keys in left and right subtrees
Node left_lca = findLCA(node.left, n1, n2);
Node right_lca = findLCA(node.right, n1, n2);
// If both of the above calls return Non-NULL,
// then one key is present in once subtree
// and other is present in other, So this
// node is the LCA
if (left_lca != null && right_lca != null)
return node;
// Otherwise check if left subtree or
// right subtree is LCA
return (left_lca != null) ? left_lca : right_lca;
}
// Driver code
public static void Main(string []args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Console.WriteLine("LCA(4, 5) = " +
tree.findLCA(4, 5).data);
Console.WriteLine("LCA(4, 6) = " +
tree.findLCA(4, 6).data);
Console.WriteLine("LCA(3, 4) = " +
tree.findLCA(3, 4).data);
Console.WriteLine("LCA(2, 4) = " +
tree.findLCA(2, 4).data);
}
}
// This code is contributed by pratham76
Javascript
<script>
// JavaScript implementation to find
// lowest common ancestor of
// n1 and n2 using one traversal of binary tree
class Node
{
constructor(item) {
this.left = null;
this.right = null;
this.data = item;
}
}
//Root of the Binary Tree
let root;
function findlCA(n1, n2)
{
return findLCA(root, n1, n2);
}
// This function returns pointer to LCA of two given
// values n1 and n2. This function assumes that n1 and
// n2 are present in Binary Tree
function findLCA(node, n1, n2)
{
// Base case
if (node == null)
return null;
// If either n1 or n2 matches with root's key, report
// the presence by returning root (Note that if a key is
// ancestor of other, then the ancestor key becomes LCA
if (node.data == n1 || node.data == n2)
return node;
// Look for keys in left and right subtrees
let left_lca = findLCA(node.left, n1, n2);
let right_lca = findLCA(node.right, n1, n2);
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca!=null && right_lca!=null)
return node;
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != null) ? left_lca : right_lca;
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
document.write("LCA(4, 5) = " +
findlCA(4, 5).data + "</br>");
document.write("LCA(4, 6) = " +
findlCA(4, 6).data + "</br>");
document.write("LCA(3, 4) = " +
findlCA(3, 4).data + "</br>");
document.write("LCA(2, 4) = " +
findlCA(2, 4).data + "</br>");
</script>
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2
Complejidad de tiempo: O(n) ya que el método realiza un recorrido de árbol simple de abajo hacia arriba.
Espacio Auxiliar: O(1)
Tenga en cuenta que el método anterior asume que las claves están presentes en Binary Tree . Si una clave está presente y la otra está ausente, devuelve la clave actual como LCA (idealmente debería haber devuelto NULL). Podemos extender este método para manejar todos los casos pasando dos variables booleanas v1 y v2. v1 se establece como verdadero cuando n1 está presente en el árbol y v2 se establece como verdadero si n2 está presente en el árbol.
C++
/* C++ program to find LCA of n1 and n2 using one traversal of Binary Tree.
It handles all cases even when n1 or n2 is not there in Binary Tree */
#include <iostream>
using namespace std;
// A Binary Tree Node
struct Node
{
struct Node *left, *right;
int key;
};
// Utility function to create a new tree Node
Node* newNode(int key)
{
Node *temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return temp;
}
// This function returns pointer to LCA of two given values n1 and n2.
// v1 is set as true by this function if n1 is found
// v2 is set as true by this function if n2 is found
struct Node *findLCAUtil(struct Node* root, int n1, int n2, bool &v1, bool &v2)
{
// Base case
if (root == NULL) return NULL;
// If either n1 or n2 matches with root's key, report the presence
// by setting v1 or v2 as true and return root (Note that if a key
// is ancestor of other, then the ancestor key becomes LCA)
if (root->key == n1)
{
v1 = true;
return root;
}
if (root->key == n2)
{
v2 = true;
return root;
}
// Look for keys in left and right subtrees
Node *left_lca = findLCAUtil(root->left, n1, n2, v1, v2);
Node *right_lca = findLCAUtil(root->right, n1, n2, v1, v2);
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca && right_lca) return root;
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != NULL)? left_lca: right_lca;
}
// Returns true if key k is present in tree rooted with root
bool find(Node *root, int k)
{
// Base Case
if (root == NULL)
return false;
// If key is present at root, or in left subtree or right subtree,
// return true;
if (root->key == k || find(root->left, k) || find(root->right, k))
return true;
// Else return false
return false;
}
// This function returns LCA of n1 and n2 only if both n1 and n2 are present
// in tree, otherwise returns NULL;
Node *findLCA(Node *root, int n1, int n2)
{
// Initialize n1 and n2 as not visited
bool v1 = false, v2 = false;
// Find lca of n1 and n2 using the technique discussed above
Node *lca = findLCAUtil(root, n1, n2, v1, v2);
// Return LCA only if both n1 and n2 are present in tree
if (v1 && v2 || v1 && find(lca, n2) || v2 && find(lca, n1))
return lca;
// Else return NULL
return NULL;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree given in the above example
Node * root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
Node *lca = findLCA(root, 4, 5);
if (lca != NULL)
cout << "LCA(4, 5) = " << lca->key;
else
cout << "Keys are not present ";
lca = findLCA(root, 4, 10);
if (lca != NULL)
cout << "\nLCA(4, 10) = " << lca->key;
else
cout << "\nKeys are not present ";
return 0;
}
Java
// Java implementation to find lowest common ancestor of
// n1 and n2 using one traversal of binary tree
// It also handles cases even when n1 and n2 are not there in Tree
/* Class containing left and right child of current node and key */
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of the Binary Tree
Node root;
static boolean v1 = false, v2 = false;
// This function returns pointer to LCA of two given
// values n1 and n2.
// v1 is set as true by this function if n1 is found
// v2 is set as true by this function if n2 is found
Node findLCAUtil(Node node, int n1, int n2)
{
// Base case
if (node == null)
return null;
//Store result in temp, in case of key match so that we can search for other key also.
Node temp=null;
// If either n1 or n2 matches with root's key, report the presence
// by setting v1 or v2 as true and return root (Note that if a key
// is ancestor of other, then the ancestor key becomes LCA)
if (node.data == n1)
{
v1 = true;
temp = node;
}
if (node.data == n2)
{
v2 = true;
temp = node;
}
// Look for keys in left and right subtrees
Node left_lca = findLCAUtil(node.left, n1, n2);
Node right_lca = findLCAUtil(node.right, n1, n2);
if (temp != null)
return temp;
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca != null && right_lca != null)
return node;
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != null) ? left_lca : right_lca;
}
// Finds lca of n1 and n2 under the subtree rooted with 'node'
Node findLCA(int n1, int n2)
{
// Initialize n1 and n2 as not visited
v1 = false;
v2 = false;
// Find lca of n1 and n2 using the technique discussed above
Node lca = findLCAUtil(root, n1, n2);
// Return LCA only if both n1 and n2 are present in tree
if (v1 && v2)
return lca;
// Else return NULL
return null;
}
/* Driver program to test above functions */
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Node lca = tree.findLCA(4, 5);
if (lca != null)
System.out.println("LCA(4, 5) = " + lca.data);
else
System.out.println("Keys are not present");
lca = tree.findLCA(4, 10);
if (lca != null)
System.out.println("LCA(4, 10) = " + lca.data);
else
System.out.println("Keys are not present");
}
}
Python3
""" Program to find LCA of n1 and n2 using one traversal of
Binary tree
It handles all cases even when n1 or n2 is not there in tree
"""
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# This function return pointer to LCA of two given values
# n1 and n2
# v1 is set as true by this function if n1 is found
# v2 is set as true by this function if n2 is found
def findLCAUtil(root, n1, n2, v):
# Base Case
if root is None:
return None
# IF either n1 or n2 matches ith root's key, report
# the presence by setting v1 or v2 as true and return
# root (Note that if a key is ancestor of other, then
# the ancestor key becomes LCA)
if root.key == n1 :
v[0] = True
return root
if root.key == n2:
v[1] = True
return root
# Look for keys in left and right subtree
left_lca = findLCAUtil(root.left, n1, n2, v)
right_lca = findLCAUtil(root.right, n1, n2, v)
# If both of the above calls return Non-NULL, then one key
# is present in once subtree and other is present in other,
# So this node is the LCA
if left_lca and right_lca:
return root
# Otherwise check if left subtree or right subtree is LCA
return left_lca if left_lca is not None else right_lca
def find(root, k):
# Base Case
if root is None:
return False
# If key is present at root, or if left subtree or right
# subtree , return true
if (root.key == k or find(root.left, k) or
find(root.right, k)):
return True
# Else return false
return False
# This function returns LCA of n1 and n2 on value if both
# n1 and n2 are present in tree, otherwise returns None
def findLCA(root, n1, n2):
# Initialize n1 and n2 as not visited
v = [False, False]
# Find lca of n1 and n2 using the technique discussed above
lca = findLCAUtil(root, n1, n2, v)
# Returns LCA only if both n1 and n2 are present in tree
if (v[0] and v[1] or v[0] and find(lca, n2) or v[1] and
find(lca, n1)):
return lca
# Else return None
return None
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
lca = findLCA(root, 4, 5)
if lca is not None:
print ("LCA(4, 5) = ", lca.key)
else :
print ("Keys are not present")
lca = findLCA(root, 4, 10)
if lca is not None:
print ("LCA(4,10) = ", lca.key)
else:
print ("Keys are not present")
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
using System;
// c# implementation to find lowest common ancestor of
// n1 and n2 using one traversal of binary tree
// It also handles cases even when n1 and n2 are not there in Tree
/* Class containing left and right child of current node and key */
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
// Root of the Binary Tree
public Node root;
public static bool v1 = false, v2 = false;
// This function returns pointer to LCA of two given
// values n1 and n2.
// v1 is set as true by this function if n1 is found
// v2 is set as true by this function if n2 is found
public virtual Node findLCAUtil(Node node, int n1, int n2)
{
// Base case
if (node == null)
{
return null;
}
//Store result in temp, in case of key match so that we can search for other key also.
Node temp = null;
// If either n1 or n2 matches with root's key, report the presence
// by setting v1 or v2 as true and return root (Note that if a key
// is ancestor of other, then the ancestor key becomes LCA)
if (node.data == n1)
{
v1 = true;
temp = node;
}
if (node.data == n2)
{
v2 = true;
temp = node;
}
// Look for keys in left and right subtrees
Node left_lca = findLCAUtil(node.left, n1, n2);
Node right_lca = findLCAUtil(node.right, n1, n2);
if (temp != null)
{
return temp;
}
// If both of the above calls return Non-NULL, then one key
// is present in once subtree and other is present in other,
// So this node is the LCA
if (left_lca != null && right_lca != null)
{
return node;
}
// Otherwise check if left subtree or right subtree is LCA
return (left_lca != null) ? left_lca : right_lca;
}
// Finds lca of n1 and n2 under the subtree rooted with 'node'
public virtual Node findLCA(int n1, int n2)
{
// Initialize n1 and n2 as not visited
v1 = false;
v2 = false;
// Find lca of n1 and n2 using the technique discussed above
Node lca = findLCAUtil(root, n1, n2);
// Return LCA only if both n1 and n2 are present in tree
if (v1 && v2)
{
return lca;
}
// Else return NULL
return null;
}
/* Driver program to test above functions */
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
Node lca = tree.findLCA(4, 5);
if (lca != null)
{
Console.WriteLine("LCA(4, 5) = " + lca.data);
}
else
{
Console.WriteLine("Keys are not present");
}
lca = tree.findLCA(4, 10);
if (lca != null)
{
Console.WriteLine("LCA(4, 10) = " + lca.data);
}
else
{
Console.WriteLine("Keys are not present");
}
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// JavaScript implementation to find lowest
// common ancestor of n1 and n2 using one
// traversal of binary tree. It also handles
// cases even when n1 and n2 are not there in Tree
// Class containing left and right child
// of current node and key
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree{
// Root of the Binary Tree
constructor()
{
this.root = null;
this.v1 = false;
this.v2 = false;
}
// This function returns pointer to LCA
// of two given values n1 and n2.
// v1 is set as true by this function
// if n1 is found
// v2 is set as true by this function
// if n2 is found
findLCAUtil(node, n1, n2)
{
// Base case
if (node == null)
{
return null;
}
// Store result in temp, in case of
// key match so that we can search
// for other key also.
var temp = null;
// If either n1 or n2 matches with root's key,
// report the presence by setting v1 or v2 as
// true and return root (Note that if a key
// is ancestor of other, then the ancestor
// key becomes LCA)
if (node.data == n1)
{
this.v1 = true;
temp = node;
}
if (node.data == n2)
{
this.v2 = true;
temp = node;
}
// Look for keys in left and right subtrees
var left_lca = this.findLCAUtil(node.left, n1, n2);
var right_lca = this.findLCAUtil(node.right, n1, n2);
if (temp != null)
{
return temp;
}
// If both of the above calls return Non-NULL,
// then one key is present in once subtree and
// other is present in other, So this node is the LCA
if (left_lca != null && right_lca != null)
{
return node;
}
// Otherwise check if left subtree or
// right subtree is LCA
return left_lca != null ? left_lca : right_lca;
}
// Finds lca of n1 and n2 under the
// subtree rooted with 'node'
findLCA(n1, n2)
{
// Initialize n1 and n2 as not visited
this.v1 = false;
this.v2 = false;
// Find lca of n1 and n2 using the
// technique discussed above
var lca = this.findLCAUtil(this.root, n1, n2);
// Return LCA only if both n1 and n2
// are present in tree
if (this.v1 && this.v2)
{
return lca;
}
// Else return NULL
return null;
}
}
// Driver code
var tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
var lca = tree.findLCA(4, 5);
if (lca != null)
{
document.write("LCA(4, 5) = " +
lca.data + "<br>");
} else
{
document.write("Keys are not present" + "<br>");
}
lca = tree.findLCA(4, 10);
if (lca != null)
{
document.write("LCA(4, 10) = " +
lca.data + "<br>");
}
else
{
document.write("Keys are not present" + "<br>");
}
// This code is contributed by rdtank
</script>
LCA(4, 5) = 2 Keys are not present
Complejidad temporal: O(n)
Espacio auxiliar: O(1)
Hemos discutido una solución eficiente para encontrar LCA en Binary Search Tree . En Binary Search Tree, utilizando las propiedades BST, podemos encontrar LCA en tiempo O(h) donde h es la altura del árbol. Tal implementación no es posible en Binary Tree ya que las claves de los Nodes de Binary Tree no siguen ningún orden.
Es posible que desee ver también los siguientes artículos:
LCA usando
el antepasado común más bajo del puntero principal en un árbol de búsqueda binaria.
Encuentre LCA en árbol binario usando RMQ
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA