Dado un árbol binario, aclárelo en una lista enlazada en el lugar. No se permite el uso de estructuras de datos auxiliares. Después de aplanar, la izquierda de cada Node debe apuntar a NULL y la derecha debe contener el siguiente Node en orden previo.
Ejemplos:
Input :
1
/ \
2 5
/ \ \
3 4 6
Output :
1
\
2
\
3
\
4
\
5
\
6
Input :
1
/ \
3 4
/
2
\
5
Output :
1
\
3
\
4
\
2
\
5
Enfoque simple: una solución simple es usar el cruce de orden de nivel usando la cola. En el recorrido de orden de niveles, realice un seguimiento del Node anterior. Haga que el Node actual sea el hijo derecho del anterior y el izquierdo del Node anterior como NULL. Esta solución requiere cola, pero la pregunta pide resolver sin estructura de datos adicional.
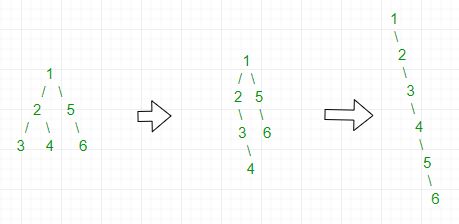
Eficiente sin estructura de datos adicional Busque recursivamente el Node sin nietos y el hijo izquierdo y derecho en el subárbol izquierdo. Luego almacene node->right en temp y haga node->right=node->left. Inserte temp en el primer Node NULL a la derecha del Node por node=node->right. Repita hasta que se convierta en una lista enlazada.
Por ejemplo,
C++
// C++ Program to flatten a given Binary Tree into linked
// list
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
Node *left, *right;
};
// utility that allocates a new Node with the given key
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return (node);
}
// Function to convert binary tree into linked list by
// altering the right node and making left node point to
// NULL
void flatten(struct Node* root)
{
// base condition- return if root is NULL or if it is a
// leaf node
if (root == NULL || root->left == NULL && root->right == NULL)
return;
// if root->left exists then we have to make it
// root->right
if (root->left != NULL) {
// move left recursively
flatten(root->left);
// store the node root->right
struct Node* tmpRight = root->right;
root->right = root->left;
root->left = NULL;
// find the position to insert the stored value
struct Node* t = root->right;
while (t->right != NULL)
t = t->right;
// insert the stored value
t->right = tmpRight;
}
// now call the same function for root->right
flatten(root->right);
}
// To find the inorder traversal
void inorder(struct Node* root)
{
// base condition
if (root == NULL)
return;
inorder(root->left);
cout << root->key << " ";
inorder(root->right);
}
/* Driver program to test above functions*/
int main()
{
/* 1
/ \
2 5
/ \ \
3 4 6 */
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(3);
root->left->right = newNode(4);
root->right->right = newNode(6);
flatten(root);
cout << "The Inorder traversal after flattening binary tree ";
inorder(root);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C Program to flatten a given Binary Tree into linked
// list
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int key;
struct Node *left, *right;
}Node;
// utility that allocates a new Node with the given key
Node* newNode(int key)
{
Node* node = (Node*)malloc(sizeof(Node));
node->key = key;
node->left = node->right = NULL;
return (node);
}
// Function to convert binary tree into linked list by
// altering the right node and making left node point to
// NULL
void flatten(Node* root)
{
// base condition- return if root is NULL or if it is a
// leaf node
if (root == NULL || root->left == NULL && root->right == NULL)
return;
// if root->left exists then we have to make it
// root->right
if (root->left != NULL) {
// move left recursively
flatten(root->left);
// store the node root->right
struct Node* tmpRight = root->right;
root->right = root->left;
root->left = NULL;
// find the position to insert the stored value
struct Node* t = root->right;
while (t->right != NULL)
t = t->right;
// insert the stored value
t->right = tmpRight;
}
// now call the same function for root->right
flatten(root->right);
}
// To find the inorder traversal
void inorder(struct Node* root)
{
// base condition
if (root == NULL)
return;
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
/* Driver program to test above functions*/
int main()
{
/* 1
/ \
2 5
/ \ \
3 4 6 */
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(3);
root->left->right = newNode(4);
root->right->right = newNode(6);
flatten(root);
printf("The Inorder traversal after flattening binary tree ");
inorder(root);
return 0;
}
// This code is contributed by aditykumar129.
Java
// Java program to flatten a given Binary Tree into linked
// list
// A binary tree node
class Node {
int data;
Node left, right;
Node(int key)
{
data = key;
left = right = null;
}
}
class BinaryTree {
Node root;
// Function to convert binary tree into linked list by
// altering the right node and making left node NULL
public void flatten(Node node)
{
// Base case - return if root is NULL
if (node == null)
return;
// Or if it is a leaf node
if (node.left == null && node.right == null)
return;
// If root.left children exists then we have to make
// it node.right (where node is root)
if (node.left != null) {
// Move left recursively
flatten(node.left);
// Store the node.right in Node named tempNode
Node tempNode = node.right;
node.right = node.left;
node.left = null;
// Find the position to insert the stored value
Node curr = node.right;
while (curr.right != null)
curr = curr.right;
// Insert the stored value
curr.right = tempNode;
}
// Now call the same function for node.right
flatten(node.right);
}
// Function for Inorder traversal
public void inOrder(Node node)
{
// Base Condition
if (node == null)
return;
inOrder(node.left);
System.out.print(node.data + " ");
inOrder(node.right);
}
// Driver code
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
/* 1
/ \
2 5
/ \ \
3 4 6 */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(3);
tree.root.left.right = new Node(4);
tree.root.right.right = new Node(6);
System.out.println(
"The Inorder traversal after flattening binary tree ");
tree.flatten(tree.root);
tree.inOrder(tree.root);
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# Python3 program to flatten a given Binary
# Tree into linked list
class Node:
def __init__(self):
self.key = 0
self.left = None
self.right = None
# Utility that allocates a new Node
# with the given key
def newNode(key):
node = Node()
node.key = key
node.left = node.right = None
return (node)
# Function to convert binary tree into
# linked list by altering the right node
# and making left node point to None
def flatten(root):
# Base condition- return if root is None
# or if it is a leaf node
if (root == None or root.left == None and
root.right == None):
return
# If root.left exists then we have
# to make it root.right
if (root.left != None):
# Move left recursively
flatten(root.left)
# Store the node root.right
tmpRight = root.right
root.right = root.left
root.left = None
# Find the position to insert
# the stored value
t = root.right
while (t.right != None):
t = t.right
# Insert the stored value
t.right = tmpRight
# Now call the same function
# for root.right
flatten(root.right)
# To find the inorder traversal
def inorder(root):
# Base condition
if (root == None):
return
inorder(root.left)
print(root.key, end = ' ')
inorder(root.right)
# Driver Code
if __name__=='__main__':
''' 1
/ \
2 5
/ \ \
3 4 6 '''
root = newNode(1)
root.left = newNode(2)
root.right = newNode(5)
root.left.left = newNode(3)
root.left.right = newNode(4)
root.right.right = newNode(6)
flatten(root)
print("The Inorder traversal after "
"flattening binary tree ",
end = '')
inorder(root)
# This code is contributed by pratham76
C#
// C# program to flatten a given
// Binary Tree into linked list
using System;
// A binary tree node
class Node
{
public int data;
public Node left, right;
public Node(int key)
{
data = key;
left = right = null;
}
}
class BinaryTree
{
Node root;
// Function to convert binary tree into
// linked list by altering the right node
// and making left node NULL
public void flatten(Node node)
{
// Base case - return if root is NULL
if (node == null)
return;
// Or if it is a leaf node
if (node.left == null &&
node.right == null)
return;
// If root.left children exists then we have
// to make it node.right (where node is root)
if (node.left != null)
{
// Move left recursively
flatten(node.left);
// Store the node.right in
// Node named tempNode
Node tempNode = node.right;
node.right = node.left;
node.left = null;
// Find the position to insert
// the stored value
Node curr = node.right;
while (curr.right != null)
{
curr = curr.right;
}
// Insert the stored value
curr.right = tempNode;
}
// Now call the same function
// for node.right
flatten(node.right);
}
// Function for Inorder traversal
public void inOrder(Node node)
{
// Base Condition
if (node == null)
return;
inOrder(node.left);
Console.Write(node.data + " ");
inOrder(node.right);
}
// Driver code
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
/* 1
/ \
2 5
/ \ \
3 4 6 */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(3);
tree.root.left.right = new Node(4);
tree.root.right.right = new Node(6);
Console.Write("The Inorder traversal after " +
"flattening binary tree ");
tree.flatten(tree.root);
tree.inOrder(tree.root);
}
}
// This code is contributed by rutvik_56
Javascript
<script>
// Javascript program to flatten a given
// Binary Tree into linked list
// A binary tree node
class Node
{
constructor(key)
{
this.data = key;
this.left = null;
this.right = null;
}
}
var root;
// Function to convert binary tree into
// linked list by altering the right node
// and making left node NULL
function flatten(node)
{
// Base case - return if root is NULL
if (node == null)
return;
// Or if it is a leaf node
if (node.left == null &&
node.right == null)
return;
// If root.left children exists then we have
// to make it node.right (where node is root)
if (node.left != null)
{
// Move left recursively
flatten(node.left);
// Store the node.right in
// Node named tempNode
var tempNode = node.right;
node.right = node.left;
node.left = null;
// Find the position to insert
// the stored value
var curr = node.right;
while (curr.right != null)
{
curr = curr.right;
}
// Insert the stored value
curr.right = tempNode;
}
// Now call the same function
// for node.right
flatten(node.right);
}
// Function for Inorder traversal
function inOrder(node)
{
// Base Condition
if (node == null)
return;
inOrder(node.left);
document.write(node.data + " ");
inOrder(node.right);
}
// Driver code
/* 1
/ \
2 5
/ \ \
3 4 6 */
root = new Node(1);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(6);
document.write("The Inorder traversal after " +
"flattening binary tree ");
flatten(root);
inOrder(root);
// This code is contributed by famously
</script>
The Inorder traversal after flattening binary tree 1 2 3 4 5 6
