Aplicación de la Derivada – Máximos y Mínimos | Matemáticas

El concepto de derivada se puede utilizar para encontrar el valor máximo y mínimo de la función dada. Sabemos que la información sobre el gradiente o la pendiente se puede derivar de la derivada de una función. Intentamos encontrar un punto que tenga gradientes cero y luego localizamos el valor máximo y mínimo cerca de él. Es útil porque se puede utilizar para maximizar las ganancias de una curva dada o minimizar pérdidas o costos según el área de uso.

Nota: Si f(x)es una función continua, entonces para cada función continua en un intervalo cerrado tiene un valor máximo y mínimo.

Sea f una función de valor real y sea a un punto interior en el dominio de f . Después
• ‘a’ se llama punto de máximos locales si hay un h > 0 tal que f(a) ≥f(x), para todo x en (a – h, a + h), x≠a El valor f( a) se llama valor máximo local de f.
• ‘a’ se llama punto de mínimos locales si hay un h > 0 tal que f(a) ≥ f(x), para todo x en (a – h, a + h) El valor f(a) se llama el valor mínimo local de f

Nota: Sea f una función definida en un intervalo abierto I . Supongamos que c ∈ Yo ser cualquier punto. Si f tiene un máximo local o un mínimo local en x = c, entonces f ^‘ (c) = 0 o f no es diferenciable en c.

Pasos para encontrar máximos y mínimos –
1. Prueba de la primera derivada
   • Si 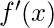cambia su signo de positivo a negativo, entonces el punto c en el que ocurre es el máximo local.
   • Si 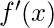cambia su signo de negativo a positivo, entonces el punto c en el que ocurre es un mínimo local.
   • Si 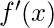no cambia su signo a medida que x aumenta a través de c, entonces el punto es el punto de inflexión.


En el diagrama anterior, C ₃ es un máximo global y C ₄ un mínimo local.

2. Prueba de la segunda derivada
   • Encuentre valores de x para los cuales 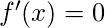estos puntos se denominan puntos críticos.
   • Encuentre 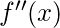y coloque los valores de x que se encontraron arriba, si
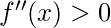     1. entonces el punto es minimo
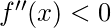     2. entonces el punto es maximo
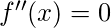     3. entonces no podemos decir nada, ahora tenemos que usar la primera derivada para verificar si el punto es punto de inflexión, mínimos locales o máximos locales.

Punto estacionario:
Un punto en el que la tangente a la gráfica es horizontal se conoce como punto estacionario, es decir, el punto en el que .

Nota: si tiene que encontrar el valor máximo y mínimo de una función en un intervalo cerrado, encuentre todos los puntos críticos igualando y luego encuentre el valor de f(x) en todos los puntos en el intervalo dado [a, b] .
 

Preguntas relacionadas con la puerta:
• Puerta CS 2012