Aptitud | PUERTA CS 1998 | Pregunta 65

una. Encuentre los puntos de máximos y mínimos locales, si los hay, de la siguiente función definida en 0≤ x ≤ 6.

  x3-6x+9x-15

b. Integrar

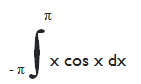
Answer:
Explanation: (a)

f(x)= x^3-6x^2+9x-15
f'(x) = 3x^2-12x+9
f''(x) = 6x-12

Para encontrar el punto crítico

Ahora f'(x) =0

3x^2-12x+9=0

Después de resolver, obtenemos

x=3 or x=1

Ahora, f”(x)= 6x-12. Poner x=3 obtenemos un valor positivo en x=3
Por lo tanto, mínimos locales =3

f”(x)= 6x-12. poner x=1 obtenemos valor negativo en x=1

Por lo tanto, máximos locales = 1

(b)

f(x)= ∫x cosx dx donde el límite superior π y el límite inferior es -π.

Aquí x es una función impar y cos x es una función par, entonces x cos x es una función impar.

Como sabemos, si g(x) es una función impar, entonces ∫g(x) dx = 0 el límite superior a y el límite inferior es -a.

Por lo tanto, f(x)= ∫x cos x dx donde el límite superior es π y el límite inferior es -π con valor 0.
Cuestionario de esta pregunta