Árbol de búsqueda binaria de doble subproceso: es un árbol de búsqueda binaria en el que los Nodes no son todos los punteros NULL de la izquierda apuntan a su predecesor en orden y el puntero NULL de la derecha apunta al sucesor en orden.
Los subprocesos también son útiles para acceder rápidamente a los ancestros de un Node.
El árbol de búsqueda binaria de doble subproceso es uno de los tipos más utilizados de estructuras de datos avanzadas que se utilizan en muchas aplicaciones en tiempo real, como lugares donde hay inserción y recorrido recientes de todos los elementos del árbol de búsqueda.
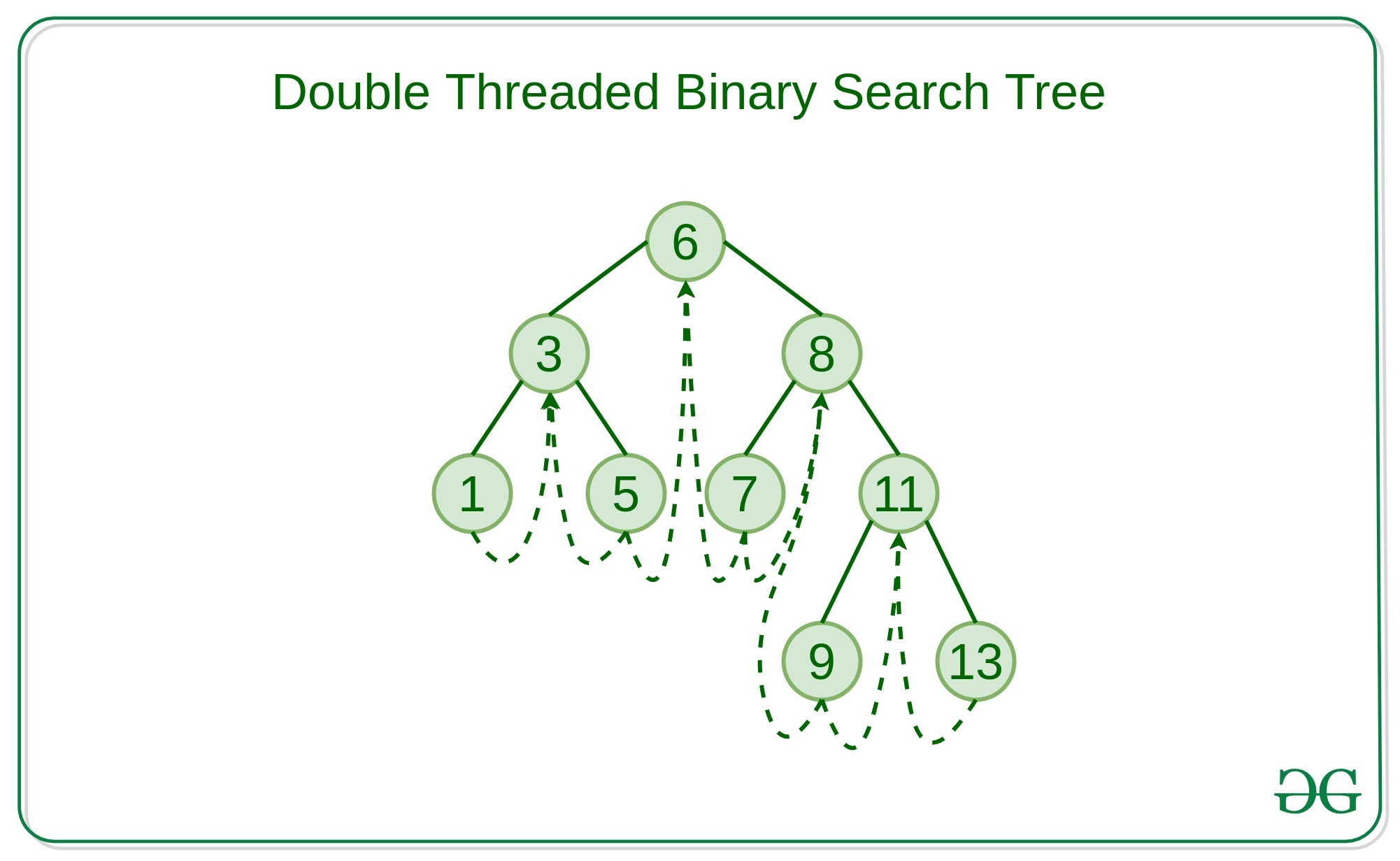
Algoritmo de creación para el árbol de búsqueda binario de doble subproceso:
- En el árbol de búsqueda binario de doble subproceso, hay cinco campos, a saber, campos de datos, punteros izquierdo y derecho, lbit y rbit, donde lbit y rbit son valores booleanos almacenados para indicar que el puntero derecho apunta a un sucesor en orden o un nuevo Node secundario. De manera similar, lbit indica que el puntero izquierdo apunta a un predecesor en orden o a un nuevo Node secundario.
- La condición base para la creación del árbol de búsqueda binaria de doble subproceso es que el Node raíz exista o no. Si no existe, cree un nuevo Node y almacénelo.
- De lo contrario, compare los datos del Node actual con los nuevos datos que se insertarán. Si los nuevos datos son menores que los datos actuales, vaya al Node secundario izquierdo. De lo contrario, vaya al Node secundario derecho.
- Si el hijo izquierdo o derecho no existe, inserte el Node a su izquierda y apunte su hijo izquierdo y derecho al predecesor en orden y al sucesor respectivamente.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the double
// threaded binary searighth tree
#include <iostream>
using namespace std;
// Class of the Node
class Node {
int lbit, rbit;
int value;
Node *left, *right;
public:
// Constructor of the
// Node of the Tree
Node()
{
lbit = rbit = 0;
value = 0;
left = right = NULL;
}
friend class DTBT;
};
// Class of the Threaded
// Binary search tree
class DTBT {
Node* root;
public:
// Constructor of the
// Threaded of the Binary
// Search Tree
DTBT()
{
root = new Node();
// Initialise the dummy node
// to any random value of
// your choice.
root->value = 9999;
// Considering our whole
// tree is at left of
// dummy node
root->rbit = 1;
root->lbit = 0;
// Consider your whole tree
// lies to the left of
// this dummy node.
root->left = root;
root->right = root;
}
void create();
void insert(int value);
void preorder();
Node* preorderSuccessor(Node*);
void inorder();
Node* inorderSuccessor(Node*);
};
// Function to create the Binary
// search tree
void DTBT::create()
{
int n = 9;
// Insertion of the nodes
this->insert(6);
this->insert(3);
this->insert(1);
this->insert(5);
this->insert(8);
this->insert(7);
this->insert(11);
this->insert(9);
this->insert(13);
}
// Function to insert the nodes
// into the threaded binary
// search tree
void DTBT::insert(int data)
{
// Condition to check if there
// is no node in the binary tree
if (root->left == root
&& root->right == root) {
Node* p = new Node();
p->value = data;
p->left = root->left;
p->lbit = root->lbit;
p->rbit = 0;
p->right = root->right;
// Inserting the node in the
// left of the dummy node
root->left = p;
root->lbit = 1;
return;
}
// New node
Node* cur = new Node;
cur = root->left;
while (1) {
// Condition to check if the
// data to be inserted is
// less than the current node
if (cur->value < data) {
Node* p = new Node();
p->value = data;
if (cur->rbit == 0) {
p->right = cur->right;
p->rbit = cur->rbit;
p->lbit = 0;
p->left = cur;
// Inserting the node
// in the right
cur->rbit = 1;
cur->right = p;
return;
}
else
cur = cur->right;
}
// Otherwise insert the node
// in the left of current node
if (cur->value > data) {
Node* p = new Node();
p->value = data;
if (cur->lbit == 0) {
p->left = cur->left;
p->lbit = cur->lbit;
p->rbit = 0;
// Pointing the right child
// to its inorder Successor
p->right = cur;
cur->lbit = 1;
cur->left = p;
return;
}
else
cur = cur->left;
}
}
}
// In Threaded binary search tree
// the left pointer of every node
// points to its Inorder predecessor,
// whereas its right pointer points
// to the the Inorder Successor
void DTBT::preorder()
{
Node* c = root->left;
// Loop to traverse the tree in
// the preorder fashion
while (c != root) {
cout << " " << c->value;
c = preorderSuccessor(c);
}
}
// Function to find the preorder
// Successor of the node
Node* DTBT::preorderSuccessor(Node* c)
{
if (c->lbit == 1) {
return c->left;
}
while (c->rbit == 0) {
c = c->right;
}
return c->right;
}
// In Threaded binary search tree
// the left pointer of every node
// points to its Inorder predecessor
// whereas its right pointer points
// to the the Inorder Successor
void DTBT::inorder()
{
Node* c;
c = root->left;
while (c->lbit == 1)
c = c->left;
// Loop to traverse the tree
while (c != root) {
cout << " " << c->value;
c = inorderSuccessor(c);
}
}
// Function to find the inorder
// successor of the node
Node* DTBT::inorderSuccessor(Node* c)
{
if (c->rbit == 0)
return c->right;
else
c = c->right;
while (c->lbit == 1) {
c = c->left;
}
return c;
}
// Driver Code
int main()
{
DTBT t1;
// Creation of the Threaded
// Binary search tree
t1.create();
cout << "Inorder Traversal of DTBST\n";
t1.inorder();
cout << "\nPreorder Traversal of DTBST\n";
t1.preorder();
return 0;
}
Inorder Traversal of DTBST 1 3 5 6 7 8 9 11 13 Preorder Traversal of DTBST 6 3 1 5 8 7 11 9 13
Publicación traducida automáticamente
Artículo escrito por rutujakawade24 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA