Árbol de chivo expiatorio | Serie 1 (Introducción e Inserción)

Un árbol ScapeGoat es un árbol de búsqueda binaria autoequilibrado como AVL Tree , Red-Black Tree , Splay Tree , etc.

• El tiempo de búsqueda es O (Log n) en el peor de los casos. El tiempo de borrado e inserción se amortiza O(Log n)
• La idea de equilibrio es asegurarse de que los Nodes estén equilibrados en tamaño α. Un tamaño equilibrado significa que los tamaños de los subárboles izquierdo y derecho son como máximo α * (Tamaño del Node). La idea se basa en el hecho de que si un Node está equilibrado en peso Α, entonces también está equilibrado en altura: altura <= log _1/&aplpha; (tamaño) + 1
• A diferencia de otros BST de equilibrio automático, el árbol ScapeGoat no requiere espacio adicional por Node. Por ejemplo, se requiere que los Nodes Red Black Tree tengan color. En la implementación a continuación de ScapeGoat Tree, solo tenemos punteros izquierdo, derecho y principal en la clase Node. El uso de padre se hace por simplicidad de implementación y puede evitarse.

Inserción (suponiendo que α = 2/3): para insertar el valor x en un árbol de chivos expiatorios:

• Cree un nuevo Node u e inserte x usando el algoritmo de inserción BST .
• Si la profundidad de u es mayor que log _3/2 n donde n es el número de Nodes en el árbol, entonces necesitamos equilibrar el árbol. Para equilibrarlo, usamos el siguiente paso para encontrar un chivo expiatorio.
  • Camine desde u hasta que lleguemos a un Node w con tamaño (w)> (2/3) * tamaño (w.parent). Este Node es el chivo expiatorio
  • Reconstruya el subárbol enraizado en w.parent.

¿Qué significa reconstruir el subárbol?  
En la reconstrucción, simplemente convertimos el subárbol al BST más equilibrado posible. Primero almacenamos el recorrido en orden de BST en una array, luego construimos una nueva BST a partir de una array dividiéndola recursivamente en dos mitades.

        60                            50
       /                           /     \
      40                          42       58
        \          Rebuild      /    \    /   \
         50       --------->  40      47 55    60
           \
            55
           /   \
         47     58
        /
      42 

A continuación se muestra la implementación en C++ de la operación de inserción en Scapegoat Tree. 

// C++ program to implement insertion in
// ScapeGoat Tree
#include<bits/stdc++.h>
using namespace std;
 
// Utility function to get value of log32(n)
static int const log32(int n)
{
  double const log23 = 2.4663034623764317;
  return (int)ceil(log23 * log(n));
}
 
// A ScapeGoat Tree node
class Node
{
public:
  Node *left, *right, *parent;
  float value;
  Node()
  {
    value = 0;
    left = right = parent = NULL;
  }
  Node (float v)
  {
    value = v;
    left = right = parent = NULL;
  }
};
 
// This functions stores inorder traversal
// of tree rooted with ptr in an array arr[]
int storeInArray(Node *ptr, Node *arr[], int i)
{
  if (ptr == NULL)
    return i;
 
  i = storeInArray(ptr->left, arr, i);
  arr[i++] = ptr;
  return storeInArray(ptr->right, arr, i);
}
 
// Class to represent a ScapeGoat Tree
class SGTree
{
private:
  Node *root;
  int n; // Number of nodes in Tree
public:
  void preorder(Node *);
  int size(Node *);
  bool insert(float x);
  void rebuildTree(Node *u);
  SGTree()   { root = NULL; n = 0; }
  void preorder() { preorder(root); }
 
  // Function to built tree with balanced nodes
  Node *buildBalancedFromArray(Node **a, int i, int n);
 
  // Height at which element is to be added
  int BSTInsertAndFindDepth(Node *u);
};
 
// Preorder traversal of the tree
void SGTree::preorder(Node *node)
{
  if (node != NULL)
  {
    cout << node->value << " ";
    preorder(node -> left);
    preorder(node -> right);
  }
}
 
// To count number of nodes in the tree
int SGTree::size(Node *node)
{
  if (node == NULL)
    return 0;
  return 1 + size(node->left) + size(node->right);
}
 
// To insert new element in the tree
bool SGTree::insert(float x)
{
  // Create a new node
  Node *node = new Node(x);
 
  // Perform BST insertion and find depth of
  // the inserted node.
  int h = BSTInsertAndFindDepth(node);
 
  // If tree becomes unbalanced
  if (h > log32(n))
  {
    // Find Scapegoat
    Node *p = node->parent;
    while (3*size(p) <= 2*size(p->parent))
      p = p->parent;
 
    // Rebuild tree rooted under scapegoat
    rebuildTree(p->parent);
  }
 
  return h >= 0;
}
 
// Function to rebuilt tree from new node. This
// function basically uses storeInArray() to
// first store inorder traversal of BST rooted
// with u in an array.
// Then it converts array to the most possible
// balanced BST using buildBalancedFromArray()
void SGTree::rebuildTree(Node *u)
{
  int n = size(u);
  Node *p = u->parent;
  Node **a = new Node* [n];
  storeInArray(u, a, 0);
  if (p == NULL)
  {
    root = buildBalancedFromArray(a, 0, n);
    root->parent = NULL;
  }
  else if (p->right == u)
  {
    p->right = buildBalancedFromArray(a, 0, n);
    p->right->parent = p;
  }
  else
  {
    p->left = buildBalancedFromArray(a, 0, n);
    p->left->parent = p;
  }
}
 
// Function to built tree with balanced nodes
Node * SGTree::buildBalancedFromArray(Node **a,
                int i, int n)
{
  if (n== 0)
    return NULL;
  int m = n / 2;
 
  // Now a[m] becomes the root of the new
  // subtree a[0],.....,a[m-1]
  a[i+m]->left = buildBalancedFromArray(a, i, m);
 
  // elements a[0],...a[m-1] gets stored
  // in the left subtree
  if (a[i+m]->left != NULL)
    a[i+m]->left->parent = a[i+m];
 
  // elements a[m+1],....a[n-1] gets stored
  // in the right subtree
  a[i+m]->right =
    buildBalancedFromArray(a, i+m+1, n-m-1);
  if (a[i+m]->right != NULL)
    a[i+m]->right->parent = a[i+m];
 
  return a[i+m];
}
 
// Performs standard BST insert and returns
// depth of the inserted node.
int SGTree::BSTInsertAndFindDepth(Node *u)
{
  // If tree is empty
  Node *w = root;
  if (w == NULL)
  {
    root = u;
    n++;
    return 0;
  }
 
  // While the node is not inserted
  // or a node with same key exists.
  bool done = false;
  int d = 0;
  do
  {
    if (u->value < w->value)
    {
      if (w->left == NULL)
      {
        w->left = u;
        u->parent = w;
        done = true;
      }
      else
        w = w->left;
    }
    else if (u->value > w->value)
    {
      if (w->right == NULL)
      {
        w->right = u;
        u->parent = w;
        done = true;
      }
      else
        w = w->right;
    }
    else
      return -1;
    d++;
  }
  while (!done);
 
  n++;
  return d;
}
 
// Driver code
int main()
{
  SGTree sgt;
  sgt.insert(7);
  sgt.insert(6);
  sgt.insert(3);
  sgt.insert(1);
  sgt.insert(0);
  sgt.insert(8);
  sgt.insert(9);
  sgt.insert(4);
  sgt.insert(5);
  sgt.insert(2);
  sgt.insert(3.5);
  printf("Preorder traversal of the"
    " constructed ScapeGoat tree is \n");
  sgt.preorder();
  return 0;
}

Preorder traversal of the constructed ScapeGoat tree is 
7 6 3 1 0 2 4 3.5 5 8 9 

Ejemplo para ilustrar la inserción:

Un árbol de chivo expiatorio con 10 Nodes y altura 5.

    
               7
             /  \
            6    8
           /      \
          5        9
        /
       2
     /  \
    1    4
   /    /  
  0    3 

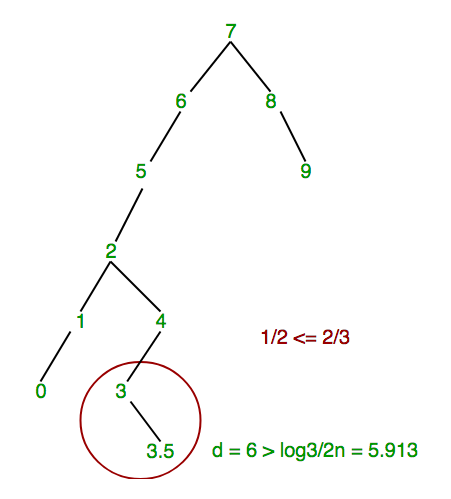
Let’s insert 3.5 in the below scapegoat tree.

Inicialmente d = 5 < log _3/2 n donde n = 10;

Dado que, d > log _3/2 n, es decir, 6 > log _3/2 n, entonces tenemos que encontrar el chivo expiatorio para resolver el problema de exceder la altura.

• Ahora encontramos un chivo expiatorio. Comenzamos con el Node 3.5 recién agregado y verificamos si el tamaño (3.5)/tamaño (3)> 2/3.
• Dado que tamaño (3,5) = 1 y tamaño (3) = 2, entonces tamaño (3,5)/tamaño (3) = ½, que es menor que 2/3. Entonces, este no es el chivo expiatorio y avanzamos.

• Dado que 3 no es el chivo expiatorio, nos movemos y verificamos la misma condición para el Node 4. Dado que tamaño (3) = 2 y tamaño (4) = 3, entonces tamaño (3)/tamaño (4) = 2/3 que no es mayor que 2/3. Entonces, este no es el chivo expiatorio y avanzamos.

• Dado que 3 no es el chivo expiatorio, nos movemos y comprobamos la misma condición para el Node 4. Dado que tamaño (3) = 2 y tamaño (4) = 3, entonces tamaño (3)/tamaño (4) = 2/3, que es no mayor a 2/3. Entonces, este no es el chivo expiatorio y avanzamos.
• Ahora, tamaño (4)/tamaño (2) = 3/6. Dado que tamaño (4) = 3 y tamaño (2) = 6, pero 3/6 sigue siendo menor que 2/3, lo que no cumple la condición de chivo expiatorio, por lo que nuevamente nos movemos hacia arriba.

• Ahora, tamaño (2)/tamaño (5) = 6/7. Dado que tamaño (2) = 6 y tamaño (5) = 7. 6/7 > 2/3 que cumple la condición de chivo expiatorio, nos detenemos aquí y, por lo tanto, el Node 5 es un chivo expiatorio.

Finalmente, después de encontrar el chivo expiatorio, la reconstrucción se llevará a cabo en el subárbol enraizado en el chivo expiatorio, es decir, en 5. Árbol final:

Comparación con otros BST autoequilibrados 

Rojo-Negro y AVL: la complejidad del tiempo de búsqueda, inserción y eliminación es O (Inicio de sesión) 

Splay Tree: en el peor de los casos, las complejidades de tiempo de búsqueda, inserción y eliminación son O (n). Pero la complejidad del tiempo amortizado de estas operaciones es O(Log n). 

ScapeGoat Tree: Al igual que Splay Tree, es fácil de implementar y tiene una complejidad de tiempo de búsqueda en el peor de los casos como O (Iniciar sesión). Las complejidades del peor de los casos y el tiempo amortizado de inserción y eliminación son las mismas que Splay Tree para Scapegoat tree. 

Este artículo es una contribución de Rahul Aggarwal y Sahil Chhabra (akku) . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.