Dado un grafo conexo y no dirigido, un árbol de expansión de ese grafo es un subgrafo que es un árbol y conecta todos los vértices entre sí. Un solo gráfico puede tener muchos árboles de expansión diferentes. Un árbol de expansión de producto mínimo para un gráfico ponderado, conectado y no dirigido es un árbol de expansión con un producto de peso menor o igual que el producto de peso de cualquier otro árbol de expansión. El producto de peso de un árbol de expansión es el producto de los pesos correspondientes a cada borde del árbol de expansión. Todos los pesos del gráfico dado serán positivos por simplicidad.
Ejemplos:

Minimum Product that we can obtain is 180 for above graph by choosing edges 0-1, 1-2, 0-3 and 1-4
Este problema se puede resolver usando algoritmos de árbol de expansión mínimo estándar como Kruskal ( https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/ ) y el algoritmo de prim , pero necesitamos para modificar nuestro gráfico para utilizar estos algoritmos. Los algoritmos de árbol de expansión mínimo intentan minimizar la suma total de pesos, aquí necesitamos minimizar el producto total de pesos. Podemos usar la propiedad de los logaritmos para superar este problema.
Como la conocemos,
log(w1* w2 * w3 * …. * wN) =
log(w1) + log(w2) + log(w3) ….. + log(wN)
Podemos reemplazar cada peso del gráfico por su valor de registro, luego aplicamos cualquier algoritmo de árbol de expansión mínimo que intentará minimizar la suma de log (wi) que a su vez minimiza el producto de peso.
Por ejemplo, el gráfico, los pasos se muestran debajo del diagrama,
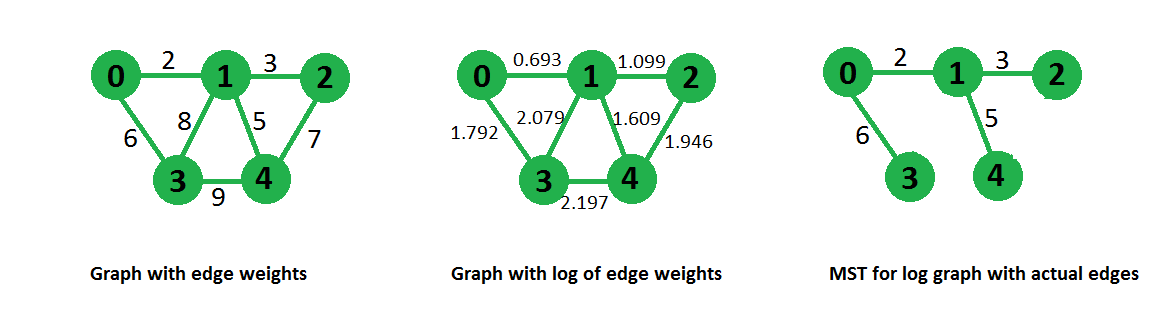
En el siguiente código primero, hemos construido el gráfico de registro a partir del gráfico de entrada dado, luego ese gráfico se proporciona como entrada al algoritmo MST de prim, que minimizará la suma total de pesos del árbol. Dado que los pesos del gráfico modificado son logaritmos del gráfico de entrada real, en realidad minimizamos el producto de los pesos del árbol de expansión.
C++
// A C++ program for getting minimum product
// spanning tree The program is for adjacency matrix
// representation of the graph
#include <bits/stdc++.h>
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[] and print Minimum Obtainable
// product
int printMST(int parent[], int n, int graph[V][V])
{
printf("Edge Weight\n");
int minProduct = 1;
for (int i = 1; i < V; i++) {
printf("%d - %d %d \n",
parent[i], i, graph[i][parent[i]]);
minProduct *= graph[i][parent[i]];
}
printf("Minimum Obtainable product is %d\n",
minProduct);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
// inputGraph is sent for printing actual edges and
// logGraph is sent for actual MST operations
void primMST(int inputGraph[V][V], double logGraph[V][V])
{
int parent[V]; // Array to store constructed MST
int key[V]; // Key values used to pick minimum
// weight edge in cut
bool mstSet[V]; // To represent set of vertices not
// yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is
// picked as first vertex
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++)
// logGraph[u][v] is non zero only for
// adjacent vertices of m mstSet[v] is false
// for vertices not yet included in MST
// Update the key only if logGraph[u][v] is
// smaller than key[v]
if (logGraph[u][v] > 0 && mstSet[v] == false && logGraph[u][v] < key[v])
parent[v] = u, key[v] = logGraph[u][v];
}
// print the constructed MST
printMST(parent, V, inputGraph);
}
// Method to get minimum product spanning tree
void minimumProductMST(int graph[V][V])
{
double logGraph[V][V];
// Constructing logGraph from original graph
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i][j] > 0)
logGraph[i][j] = log(graph[i][j]);
else
logGraph[i][j] = 0;
}
}
// Applying standard Prim's MST algorithm on
// Log graph.
primMST(graph, logGraph);
}
// driver program to test above function
int main()
{
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int graph[V][V] = {
{ 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 },
};
// Print the solution
minimumProductMST(graph);
return 0;
}
Java
// A Java program for getting minimum product
// spanning tree The program is for adjacency matrix
// representation of the graph
import java.util.*;
class GFG {
// Number of vertices in the graph
static int V = 5;
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
static int minKey(int key[], boolean[] mstSet)
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index = 0;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[] and print Minimum Obtainable
// product
static void printMST(int parent[], int n, int graph[][])
{
System.out.printf("Edge Weight\n");
int minProduct = 1;
for (int i = 1; i < V; i++) {
System.out.printf("%d - %d %d \n",
parent[i], i, graph[i][parent[i]]);
minProduct *= graph[i][parent[i]];
}
System.out.printf("Minimum Obtainable product is %d\n",
minProduct);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
// inputGraph is sent for printing actual edges and
// logGraph is sent for actual MST operations
static void primMST(int inputGraph[][], double logGraph[][])
{
int[] parent = new int[V]; // Array to store constructed MST
int[] key = new int[V]; // Key values used to pick minimum
// weight edge in cut
boolean[] mstSet = new boolean[V]; // To represent set of vertices not
// yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is
// picked as first vertex
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++) // logGraph[u][v] is non zero only for
// adjacent vertices of m mstSet[v] is false
// for vertices not yet included in MST
// Update the key only if logGraph[u][v] is
// smaller than key[v]
{
if (logGraph[u][v] > 0
&& mstSet[v] == false
&& logGraph[u][v] < key[v]) {
parent[v] = u;
key[v] = (int)logGraph[u][v];
}
}
}
// print the constructed MST
printMST(parent, V, inputGraph);
}
// Method to get minimum product spanning tree
static void minimumProductMST(int graph[][])
{
double[][] logGraph = new double[V][V];
// Constructing logGraph from original graph
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i][j] > 0) {
logGraph[i][j] = Math.log(graph[i][j]);
}
else {
logGraph[i][j] = 0;
}
}
}
// Applying standard Prim's MST algorithm on
// Log graph.
primMST(graph, logGraph);
}
// Driver code
public static void main(String[] args)
{
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int graph[][] = {
{ 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 },
};
// Print the solution
minimumProductMST(graph);
}
}
// This code has been contributed by 29AjayKumar
Python3
# A Python3 program for getting minimum
# product spanning tree The program is
# for adjacency matrix representation
# of the graph
import math
# Number of vertices in the graph
V = 5
# A utility function to find the vertex
# with minimum key value, from the set
# of vertices not yet included in MST
def minKey(key, mstSet):
# Initialize min value
min = 10000000
min_index = 0
for v in range(V):
if (mstSet[v] == False and
key[v] < min):
min = key[v]
min_index = v
return min_index
# A utility function to print the constructed
# MST stored in parent[] and print Minimum
# Obtainable product
def printMST(parent, n, graph):
print("Edge Weight")
minProduct = 1
for i in range(1, V):
print("{} - {} {} ".format(parent[i], i,
graph[i][parent[i]]))
minProduct *= graph[i][parent[i]]
print("Minimum Obtainable product is {}".format(
minProduct))
# Function to construct and print MST for
# a graph represented using adjacency
# matrix representation inputGraph is
# sent for printing actual edges and
# logGraph is sent for actual MST
# operations
def primMST(inputGraph, logGraph):
# Array to store constructed MST
parent = [0 for i in range(V)]
# Key values used to pick minimum
key = [10000000 for i in range(V)]
# weight edge in cut
# To represent set of vertices not
mstSet = [False for i in range(V)]
# Yet included in MST
# Always include first 1st vertex in MST
# Make key 0 so that this vertex is
key[0] = 0
# Picked as first vertex
# First node is always root of MST
parent[0] = -1
# The MST will have V vertices
for count in range(0, V - 1):
# Pick the minimum key vertex from
# the set of vertices not yet
# included in MST
u = minKey(key, mstSet)
# Add the picked vertex to the MST Set
mstSet[u] = True
# Update key value and parent index
# of the adjacent vertices of the
# picked vertex. Consider only those
# vertices which are not yet
# included in MST
for v in range(V):
# logGraph[u][v] is non zero only
# for adjacent vertices of m
# mstSet[v] is false for vertices
# not yet included in MST. Update
# the key only if logGraph[u][v] is
# smaller than key[v]
if (logGraph[u][v] > 0 and
mstSet[v] == False and
logGraph[u][v] < key[v]):
parent[v] = u
key[v] = logGraph[u][v]
# Print the constructed MST
printMST(parent, V, inputGraph)
# Method to get minimum product spanning tree
def minimumProductMST(graph):
logGraph = [[0 for j in range(V)]
for i in range(V)]
# Constructing logGraph from
# original graph
for i in range(V):
for j in range(V):
if (graph[i][j] > 0):
logGraph[i][j] = math.log(graph[i][j])
else:
logGraph[i][j] = 0
# Applying standard Prim's MST algorithm
# on Log graph.
primMST(graph, logGraph)
# Driver code
if __name__=='__main__':
''' Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 '''
graph = [ [ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ], ]
# Print the solution
minimumProductMST(graph)
# This code is contributed by rutvik_56
C#
// C# program for getting minimum product
// spanning tree The program is for adjacency matrix
// representation of the graph
using System;
class GFG {
// Number of vertices in the graph
static int V = 5;
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
static int minKey(int[] key, Boolean[] mstSet)
{
// Initialize min value
int min = int.MaxValue, min_index = 0;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[] and print Minimum Obtainable
// product
static void printMST(int[] parent, int n, int[, ] graph)
{
Console.Write("Edge Weight\n");
int minProduct = 1;
for (int i = 1; i < V; i++) {
Console.Write("{0} - {1} {2} \n",
parent[i], i, graph[i, parent[i]]);
minProduct *= graph[i, parent[i]];
}
Console.Write("Minimum Obtainable product is {0}\n",
minProduct);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
// inputGraph is sent for printing actual edges and
// logGraph is sent for actual MST operations
static void primMST(int[, ] inputGraph, double[, ] logGraph)
{
int[] parent = new int[V]; // Array to store constructed MST
int[] key = new int[V]; // Key values used to pick minimum
// weight edge in cut
Boolean[] mstSet = new Boolean[V]; // To represent set of vertices not
// yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++) {
key[i] = int.MaxValue;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is
// picked as first vertex
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++) // logGraph[u, v] is non zero only for
// adjacent vertices of m mstSet[v] is false
// for vertices not yet included in MST
// Update the key only if logGraph[u, v] is
// smaller than key[v]
{
if (logGraph[u, v] > 0
&& mstSet[v] == false
&& logGraph[u, v] < key[v]) {
parent[v] = u;
key[v] = (int)logGraph[u, v];
}
}
}
// print the constructed MST
printMST(parent, V, inputGraph);
}
// Method to get minimum product spanning tree
static void minimumProductMST(int[, ] graph)
{
double[, ] logGraph = new double[V, V];
// Constructing logGraph from original graph
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i, j] > 0) {
logGraph[i, j] = Math.Log(graph[i, j]);
}
else {
logGraph[i, j] = 0;
}
}
}
// Applying standard Prim's MST algorithm on
// Log graph.
primMST(graph, logGraph);
}
// Driver code
public static void Main(String[] args)
{
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int[, ] graph = {
{ 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 },
};
// Print the solution
minimumProductMST(graph);
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// A Javascript program for getting minimum product
// spanning tree The program is for adjacency matrix
// representation of the graph
// Number of vertices in the graph
let V = 5;
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
function minKey(key,mstSet)
{
// Initialize min value
let min = Number.MAX_VALUE, min_index = 0;
for (let v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[] and print Minimum Obtainable
// product
function printMST(parent,n,graph)
{
document.write("Edge Weight<br>");
let minProduct = 1;
for (let i = 1; i < V; i++) {
document.write( parent[i]+" - "+ i+" " +graph[i][parent[i]]+"<br>");
minProduct *= graph[i][parent[i]];
}
document.write("Minimum Obtainable product is ",
minProduct+"<br>");
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
// inputGraph is sent for printing actual edges and
// logGraph is sent for actual MST operations
function primMST(inputGraph,logGraph)
{
let parent = new Array(V); // Array to store constructed MST
let key = new Array(V); // Key values used to pick minimum
// weight edge in cut
let mstSet = new Array(V); // To represent set of vertices not
// yet included in MST
// Initialize all keys as INFINITE
for (let i = 0; i < V; i++) {
key[i] = Number.MAX_VALUE;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is
// picked as first vertex
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (let count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
let u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not yet
// included in MST
for (let v = 0; v < V; v++) // logGraph[u][v] is non zero only for
// adjacent vertices of m mstSet[v] is false
// for vertices not yet included in MST
// Update the key only if logGraph[u][v] is
// smaller than key[v]
{
if (logGraph[u][v] > 0
&& mstSet[v] == false
&& logGraph[u][v] < key[v]) {
parent[v] = u;
key[v] = logGraph[u][v];
}
}
}
// print the constructed MST
printMST(parent, V, inputGraph);
}
// Method to get minimum product spanning tree
function minimumProductMST(graph)
{
let logGraph = new Array(V);
// Constructing logGraph from original graph
for (let i = 0; i < V; i++) {
logGraph[i]=new Array(V);
for (let j = 0; j < V; j++) {
if (graph[i][j] > 0) {
logGraph[i][j] = Math.log(graph[i][j]);
}
else {
logGraph[i][j] = 0;
}
}
}
// Applying standard Prim's MST algorithm on
// Log graph.
primMST(graph, logGraph);
}
// Driver code
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
let graph = [
[ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ],
];
// Print the solution
minimumProductMST(graph);
// This code is contributed by rag2127
</script>
Producción:
Edge Weight 0 - 1 2 1 - 2 3 0 - 3 6 1 - 4 5 Minimum Obtainable product is 180
Este artículo es una contribución de Utkarsh Trivedi . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA