Árbol de expansión disjunto de borde máximo posible de un gráfico completo

Dar un gráfico completo con N-vértices. La tarea es encontrar el número máximo posible de árbol de expansión disjunto de aristas.
El árbol de expansión disjunto de aristas es un árbol de expansión en el que no hay dos árboles en el conjunto que tengan una arista en común.
Ejemplos: 
 

Input : N = 4
Output : 2

Input : N = 5
Output : 2 

El número máximo de árboles de expansión Edge-Disjoint posibles de un gráfico completo con N vértices se puede dar como, 
 

Max Edge-disjoint spanning tree = floor(N / 2)

Veamos algunos ejemplos:
Ejemplo 1 :
 

Gráfico completo con 4 vértices

Todos los árboles de expansión disjuntos de borde posibles para el gráfico anterior son: 
 

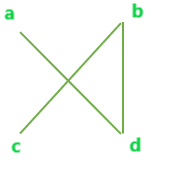
A

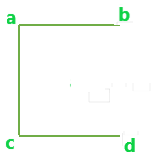
B

Ejemplo 2 : 
 

Gráfico completo con 5 vértices

Todos los árboles de expansión disjuntos de borde posibles para el gráfico anterior son: 
 

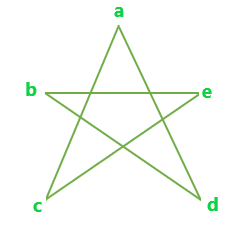
A

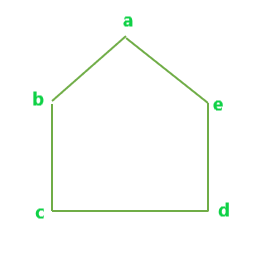
B

A continuación se muestra el programa para encontrar el número máximo posible de árboles de expansión disjuntos por aristas. 
 

// C++ program to find the maximum number of
// Edge-Disjoint Spanning tree possible
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
float edgeDisjoint(int n)
{
    float result = 0;
 
    result = floor(n / 2);
 
    return result;
}
 
// Driver code
int main()
{
    int n = 4;
 
    cout << edgeDisjoint(n);
 
    return 0;
}

// Java program to find the maximum 
// number of Edge-Disjoint Spanning
// tree possible
import java.io.*;
 
class GFG
{
     
// Function to calculate max number
// of Edge-Disjoint Spanning tree
// possible
static double edgeDisjoint(int n)
{
    double result = 0;
 
    result = Math.floor(n / 2);
 
    return result;
}
 
// Driver Code
public static void main(String[] args)
{
    int n = 4;
    System.out.println((int)edgeDisjoint(n));
}
}
 
// This code is contributed
// by Naman_Garg

# Python 3 to find the maximum
# number of Edge-Disjoint
# Spanning tree possible
import math
 
# Function to calculate max
# number of Edge-Disjoint
# Spanning tree possible
def edgeDisjoint(n):
 
    result = 0
 
    result = math.floor(n / 2)
 
    return result
 
# Driver Code
if __name__ == "__main__" :
 
    n = 4
 
    print(int(edgeDisjoint(n)))
 
# This Code is contributed
# by Naman_Garg

// C# program to find the maximum number of
// Edge-Disjoint Spanning tree possible
using System;
 
class GFG
{
 
// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
static double edgeDisjoint(double n)
{
    double result = 0;
 
    result = Math.Floor(n / 2);
 
    return result;
}
 
// Driver Code
public static void Main()
{
    int n = 4;
 
    Console.Write(edgeDisjoint(n));
}
}
 
// This code is contributed
// by Sanjit_Prasad

<?php
// PHP program to find the maximum
// number of Edge-Disjoint Spanning
// tree possible
 
// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
function edgeDisjoint($n)
{
    $result = 0;
 
    $result = floor($n / 2);
 
    return $result;
}
 
// Driver code
$n = 4;
 
echo edgeDisjoint($n);
 
// This code is contributed
// by Ankita Saini
?>

<script>
 
// Javascript program to find the maximum number of
// Edge-Disjoint Spanning tree possible
 
// Function to calculate max number of
// Edge-Disjoint Spanning tree possible
function edgeDisjoint(n)
{
    var result = 0;
 
    result = Math.floor(n / 2);
 
    return result;
}
 
// Driver code
var n = 4;
document.write( edgeDisjoint(n));
 
</script>

2