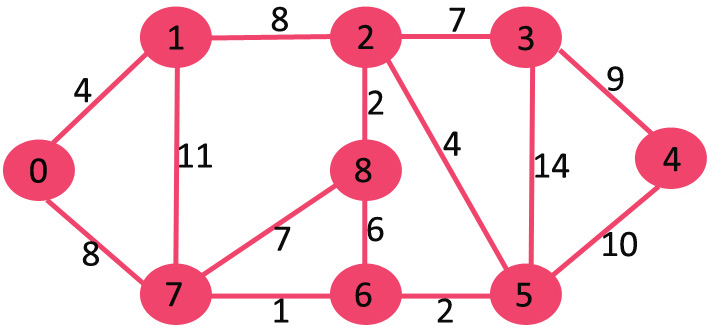
Dado un gráfico ponderado (positivo) bidirigido sin bucles automáticos, la tarea es generar el árbol de expansión mínimo del gráfico.
Ejemplos:
Entrada: N = 9, E = 14, bordes = {{0, 1, 4}, {0, 7, 8}, {1, 2, 8}, {1, 7, 11}, {2, 3, 7}, {2, 8, 2}, {2, 5, 4}, {3, 4, 9}, {3, 5, 14}, {4, 5, 10}, {5, 6, 2} , {6, 7, 1}, {6, 8, 6}, {7, 8, 7}}
Salida:
((A, B), Costo)
((6, 7), 1)
((6, 5 ), 2)
((1, 0), 4)
((2, 3), 7)
((5, 2), 4)
((3, 4), 9)
((2, 1), 8)
( (2, 8), 2)
Se ha generado un gráfico no dirigido que consta de todos los vértices V y (V-1) aristas
Entrada: N = 6, E = 14, aristas = {{0, 2, 103}, {0, 1, 158}, {0 , 2, 2}, {0, 5, 17}, {1, 3, 42}, {2, 4, 187}, {3, 0, 14}, {3, 2, 158}, {3, 5 , 106}, {3, 4, 95}, {5, 1, 144}, {5, 2, 194}, {5, 3, 118}, {5, 3, 58}} Salida: ((
A
, B), Costo)
((0, 2), 2)
((0, 3), 14)
((0, 5), 17)
((3, 1), 42)
((3, 4), 95)
Acercarse
- Primero, el borde que tiene el costo/peso mínimo se encuentra en el gráfico dado.
- Los dos vértices iniciales (vértice A, B del borde de costo mínimo) se agregan al conjunto visitado/agregado.
- Ahora, todos los bordes conectados con vértices recién agregados se agregan a la cola de prioridad.
- El vértice de menor costo (agregue todos los bordes conectados del vértice pop a la cola de prioridad) se extrae de la cola de prioridad y se repite hasta que el número de bordes sea igual a vértices-1.
- Al utilizar el tiempo de cola de prioridad, la complejidad se reducirá a (O(E log V)) donde E es el número de aristas y V es el número de vértices.
- La clase de par también se usa para almacenar los pesos.
A continuación se muestra la implementación del enfoque anterior:
Java
// Java implementation of the approach
import java.io.*;
import java.util.*;
import java.lang.Comparable;
public class MST {
// Pair class with implemented comparable
static class Pair<U extends Comparable<U>,
V extends Comparable<V> >
implements Comparable<Pair<U, V> > {
public final U a;
public final V b;
private Pair(U a, V b)
{
this.a = a;
this.b = b;
}
@Override
public boolean equals(Object o)
{
if (this == o)
return true;
if (o == null || getClass() != o.getClass())
return false;
Pair<?, ?> pair = (Pair<?, ?>)o;
if (!a.equals(pair.a))
return false;
return b.equals(pair.b);
}
// Overriding so that objects in map
// could find the object key
@Override
public int hashCode()
{
return 31 * a.hashCode() + b.hashCode();
}
@Override
public String toString()
{
return "(" + a + ", " + b + ")";
}
@Override
public int compareTo(Pair<U, V> o)
{
return getV().compareTo(o.getV());
}
private U getU()
{
return a;
}
private V getV()
{
return b;
}
}
static class Graph {
int vertices;
ArrayList[] edges;
// This variable keeps the least cost edge
static Pair<Pair<Integer, Integer>,
Integer>
minCostEdge;
Graph(int vertices)
{
minCostEdge = new Pair<>(new Pair<>(1, 1),
Integer.MAX_VALUE);
this.vertices = vertices;
edges = new ArrayList[vertices + 1];
for (int i = 0; i <= vertices; i++) {
edges[i]
= new ArrayList<Pair<Integer, Integer> >();
}
}
void addEdge(int a, int b, int weight)
{
edges[a].add(new Pair<>(b, weight));
// Since its undirected, adding the
// edges to both the vertices
edges[b].add(new Pair<>(a, weight));
if (weight < minCostEdge.b) {
minCostEdge
= new Pair<>(new Pair<>(a, b), weight);
}
}
void MST()
{
// Priority queue for applying heap
PriorityQueue<Pair<Pair<Integer, Integer>,
Integer> >
priorityQueue
= new PriorityQueue<>();
// Adding all the connected vertices
// of MinCostEdge vertex A to PQ
Iterator<Pair<Integer, Integer> > iterator
= edges[minCostEdge.a.a].listIterator();
while (iterator.hasNext()) {
Pair<Integer, Integer> pair
= iterator.next();
priorityQueue.add(
new Pair<>(
new Pair<>(minCostEdge.a.a, pair.a),
pair.b));
}
// Adding all the connected vertices
// of MinCostEdge vertex B to PQ
iterator = edges[minCostEdge.a.b].listIterator();
while (iterator.hasNext()) {
Pair<Integer, Integer> pair = iterator.next();
priorityQueue.add(
new Pair<>(
new Pair<>(minCostEdge.a.b, pair.a),
pair.b));
}
// Set to check vertex is added or not
Set<Integer> addedVertices = new HashSet<>();
// Set contains all the added edges and cost from source
Set<Pair<Pair<Integer, Integer>, Integer> > addedEdges
= new HashSet<>();
// Using the greedy approach to find
// the least costing edge to the GRAPH
while (addedEdges.size() < vertices - 1) {
// Polling from priority queue
Pair<Pair<Integer, Integer>, Integer> pair
= priorityQueue.poll();
// Checking whether the vertex A is added or not
if (!addedVertices.contains(pair.a.a)) {
addedVertices.add(pair.a.a);
addedEdges.add(pair);
// Adding all the connected vertices with vertex A
iterator = edges[pair.a.a].listIterator();
while (iterator.hasNext()) {
Pair<Integer, Integer> pair1
= iterator.next();
priorityQueue.add(
new Pair<>(
new Pair<>(pair.a.a, pair1.a),
pair1.b));
}
}
// Checking whether the vertex B is added or not
if (!addedVertices.contains(pair.a.b)) {
addedVertices.add(pair.a.b);
addedEdges.add(pair);
// Adding all the connected vertices with vertex B
iterator = edges[pair.a.b].listIterator();
while (iterator.hasNext()) {
Pair<Integer, Integer> pair1
= iterator.next();
priorityQueue
.add(
new Pair<>(
new Pair<>(pair.a.b, pair1.a),
pair1.b));
}
}
}
// Printing the MST
Iterator<Pair<Pair<Integer, Integer>, Integer> > iterator1
= addedEdges.iterator();
System.out.println("((A"
+ ", "
+ "B)"
+ ", "
+ "Cost)");
while (iterator1.hasNext()) {
System.out.println(iterator1.next());
}
}
}
// Driver code
public static void main(String[] args) throws IOException
{
// Initializing the graph
Graph g = new Graph(9);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
// Applying MST
g.MST();
}
}
((A, B), Cost) ((6, 7), 1) ((6, 5), 2) ((1, 0), 4) ((2, 3), 7) ((5, 2), 4) ((3, 4), 9) ((2, 1), 8) ((2, 8), 2)