El árbol de expresión es un árbol binario en el que cada Node interno corresponde al operador y cada Node hoja corresponde al operando, por lo que, por ejemplo, el árbol de expresión para 3 + ((5+9)*2) sería:
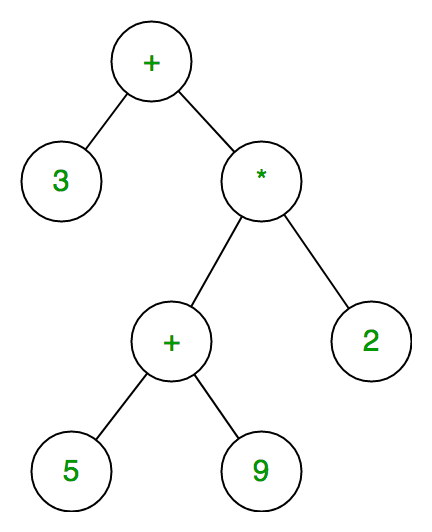
El recorrido en orden del árbol de expresión produce una versión infija de la expresión de sufijo dada (lo mismo con el recorrido en orden posterior da una expresión de sufijo)
Evaluando la expresión representada por un árbol de expresión:
Let t be the expression tree
If t is not null then
If t.value is operand then
Return t.value
A = solve(t.left)
B = solve(t.right)
// calculate applies operator 't.value'
// on A and B, and returns value
Return calculate(A, B, t.value)
Construcción del árbol de expresión:
Ahora, para construir un árbol de expresión, usamos una pila. Recorremos la expresión de entrada y hacemos lo siguiente para cada carácter.
- Si un carácter es un operando, introdúzcalo en la pila.
- Si un personaje es un operador, saque dos valores de la pila, conviértalos en su hijo y empuje el Node actual nuevamente.
Al final, el único elemento de la pila será la raíz de un árbol de expresión.
Ejemplos:
Input: A B C*+ D/ Output: A + B * C / D
Los primeros tres símbolos son operandos, así que cree Nodes de árbol y coloque punteros en ellos en una pila como se muestra a continuación.
En el siguiente paso, se leerá un operador ‘*’, por lo que se extraen dos punteros a los árboles, se forma un nuevo árbol y se empuja un puntero a la pila.

En el siguiente paso, se leerá un operador ‘+’, por lo que se extraen dos punteros a los árboles, se forma un nuevo árbol y se coloca un puntero en la pila.
A3f.png
De manera similar, como en los casos anteriores, primero empujamos ‘D’ en la pila y luego en el último paso primero, leeremos ‘/’ y luego, como el paso anterior, aparecerá el elemento superior y luego será el subárbol derecho de raíz ‘/’ y otro los Nodes serán el subárbol derecho.
El árbol de expresiones construidas final es:
A4f.png
A continuación se muestra el código del enfoque anterior:
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for expression tree
#include <bits/stdc++.h>
using namespace std;
class node {
public:
char value;
node* left;
node* right;
node* next = NULL;
node(char c)
{
this->value = c;
left = NULL;
right = NULL;
}
node()
{
left = NULL;
right = NULL;
}
friend class Stack;
friend class expression_tree;
};
class Stack {
node* head = NULL;
public:
void push(node*);
node* pop();
friend class expression_tree;
};
class expression_tree {
public:
void inorder(node* x)
{
// cout<<"Tree in InOrder Traversal is: "<<endl;
if (x == NULL)
return;
else {
inorder(x->left);
cout << x->value << " ";
inorder(x->right);
}
}
};
void Stack::push(node* x)
{
if (head == NULL) {
head = x;
}
// We are inserting here nodes at the top of the stack [following LIFO principle]
else {
x->next = head;
head = x;
}
}
node* Stack::pop()
{
// Popping out the top most[ pointed with head] element
node* p = head;
head = head->next;
return p;
}
int main()
{
string s = "ABC*+D/";
// If you wish take input from user:
//cout << "Insert Postorder Expression: " << endl;
//cin >> s;
Stack e;
expression_tree a;
node *x, *y, *z;
int l = s.length();
for (int i = 0; i < l; i++) {
// if read character is operator then popping two
// other elements from stack and making a binary
// tree
if (s[i] == '+' || s[i] == '-' || s[i] == '*'
|| s[i] == '/' || s[i] == '^') {
z = new node(s[i]);
x = e.pop();
y = e.pop();
z->left = y;
z->right = x;
e.push(z);
}
else {
z = new node(s[i]);
e.push(z);
}
}
cout << " The Inorder Traversal of Expression Tree: ";
a.inorder(z);
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
char data;
struct node* left;
struct node* right;
struct node* next;
};
struct node *head=NULL;
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(char data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
node->next = NULL;
return (node);
}
void printInorder(struct node* node)
{
if (node == NULL)
return;
else{
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%c ", node->data);
/* now recur on right child */
printInorder(node->right);
}
}
void push(struct node* x)
{
if(head==NULL)
head = x;
else
{
(x)->next = head;
head = x;
}
// struct node* temp;
// while(temp!=NULL)
// {
// printf("%c ", temp->data);
// temp = temp->next;
// }
}
struct node* pop()
{
// Poping out the top most[ pointed with head] element
struct node* p = head;
head = head->next;
return p;
}
int main()
{
char s[] = {'A','B','C','*','+','D','/'};
int l = sizeof(s) / sizeof(s[0]) ;
struct node *x, *y, *z;
for (int i = 0; i < l; i++) {
// if read character is operator then poping two
// other elements from stack and making a binary
// tree
if (s[i] == '+' || s[i] == '-' || s[i] == '*'
|| s[i] == '/' || s[i] == '^') {
z = newNode(s[i]);
x = pop();
y = pop();
z->left = y;
z->right = x;
push(z);
}
else {
z = newNode(s[i]);
push(z);
}
}
printf(" The Inorder Traversal of Expression Tree: ");
printInorder(z);
return 0;
}
Java
import java.util.Stack;
class Node{
char data;
Node left,right;
public Node(char data){
this.data = data;
left = right = null;
}
}
public class Main {
public static boolean isOperator(char ch){
if(ch=='+' || ch=='-'|| ch=='*' || ch=='/' || ch=='^'){
return true;
}
return false;
}
public static Node expressionTree(String postfix){
Stack<Node> st = new Stack<Node>();
Node t1,t2,temp;
for(int i=0;i<postfix.length();i++){
if(!isOperator(postfix.charAt(i))){
temp = new Node(postfix.charAt(i));
st.push(temp);
}
else{
temp = new Node(postfix.charAt(i));
t1 = st.pop();
t2 = st.pop();
temp.left = t2;
temp.right = t1;
st.push(temp);
}
}
temp = st.pop();
return temp;
}
public static void inorder(Node root){
if(root==null) return;
inorder(root.left);
System.out.print(root.data);
inorder(root.right);
}
public static void main(String[] args) {
String postfix = "ABC*+D/";
Node r = expressionTree(postfix);
inorder(r);
}
}
C#
using System;
using System.Collections.Generic;
class Node{
public char data;
public Node left,right;
public Node(char data){
this.data = data;
left = right = null;
}
}
public class GFG {
public static bool isOperator(char ch){
if(ch=='+' || ch=='-'|| ch=='*' || ch=='/' || ch=='^'){
return true;
}
return false;
}
static Node expressionTree(String postfix){
Stack<Node> st = new Stack<Node>();
Node t1, t2, temp;
for(int i = 0; i < postfix.Length; i++)
{
if(!isOperator(postfix[i])){
temp = new Node(postfix[i]);
st.Push(temp);
}
else{
temp = new Node(postfix[i]);
t1 = st.Pop();
t2 = st.Pop();
temp.left = t2;
temp.right = t1;
st.Push(temp);
}
}
temp = st.Pop();
return temp;
}
static void inorder(Node root){
if(root == null) return;
inorder(root.left);
Console.Write(root.data);
inorder(root.right);
}
public static void Main(String[] args)
{
String postfix = "ABC*+D/";
Node r = expressionTree(postfix);
inorder(r);
}
}
// This code is contributed by 29AjayKumar
The Inorder Traversal of Expression Tree: A + B * C / D
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
