Dada una array rectangular M[0…n-1][0…m-1] , y se solicitan consultas para encontrar la suma / mínimo / máximo en algunos sub-rectángulos M[a…b][e…f] , como así como consultas para la modificación de elementos de array individuales (es decir , M[x] [y] = p ).
También podemos responder consultas de subarrays utilizando el árbol indexado binario bidimensional .
En este artículo, nos centraremos en resolver consultas de subarrays utilizando un árbol de segmentos de dos dimensiones. El árbol de segmentos de dos dimensiones no es más que un árbol de segmentos de árboles de segmentos.
Requisito previo: Árbol de segmentos: suma del rango dado
Algoritmo :
Construiremos un árbol bidimensional de segmentos por el siguiente principio:
1 . En el primer paso, construiremos un árbol de segmentos unidimensional ordinario, trabajando solo con la primera coordenada, digamos ‘x’ e ‘y’ como constante. Aquí, no escribiremos un número dentro del Node como en el árbol de segmentos unidimensional, sino un árbol completo de segmentos.
2. El segundo paso es combinar los valores de los árboles segmentados. Supongamos que en el segundo paso, en lugar de combinar los elementos, estamos combinando los árboles de segmentos obtenidos en el primer paso.
Considere el siguiente ejemplo. Supongamos que tenemos que encontrar la suma de todos los números dentro del área roja resaltada

Paso 1: Primero crearemos el árbol de segmentos de cada franja del eje y. Aquí representamos el árbol de segmentos como una array donde el Node secundario es 2n y 2n+1 donde n > 0.
Árbol de segmentos para la franja y=1
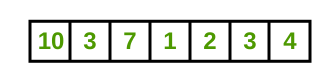
Árbol de segmentos para tira y = 2

Árbol de segmentos para tira y = 3

Árbol de segmentos para tira y = 4

Paso 2: En este paso, creamos el árbol de segmentos para la array rectangular donde el Node base son las tiras del eje y dadas anteriormente. La tarea es fusionar los árboles de segmentos anteriores.

Consulta de suma:

Gracias a Sahil Bansal por aportar esta imagen.
Consulta de procesamiento:
Responderemos a la consulta bidimensional por el siguiente principio: primero romper la consulta en la primera coordenada, y luego, cuando llegamos a algún vértice del árbol de segmentos con la primera coordenada y luego llamamos a la correspondiente árbol de segmentos en la segunda coordenada.
Esta función trabaja en tiempo O(logn*log m) , porque primero desciende por el árbol en la primera coordenada, y por cada vértice recorrido de ese árbol, hace una consulta desde el árbol habitual de segmentos a lo largo de la segunda coordenada.
Consulta de modificación:
Queremos aprender a modificar el árbol de segmentos de acuerdo con el cambio en el valor de un elemento M[x] [y] = p . Es claro que los cambios ocurrirán solo en aquellos vértices del primero árbol de segmentos que cubren la coordenada x, y para los árboles de los segmentos correspondientes a ellos, los cambios sólo ocurrirán en aquellos vértices que cubren la coordenada y. Por lo tanto, la implementación de la solicitud de modificación no será muy diferente del caso unidimensional, solo que ahora primero descenderemos la primera coordenada y luego la segunda.
Output for the highlighted area will be 25.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for implementation
// of 2D segment tree.
#include <bits/stdc++.h>
using namespace std;
// Base node of segment tree.
int ini_seg[1000][1000] = { 0 };
// final 2d-segment tree.
int fin_seg[1000][1000] = { 0 };
// Rectangular matrix.
int rect[4][4] = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 7, 5, 9 },
{ 3, 0, 6, 2 },
};
// size of x coordinate.
int size = 4;
/*
* A recursive function that constructs
* Initial Segment Tree for array rect[][] = { }.
* 'pos' is index of current node in segment
* tree seg[]. 'strip' is the enumeration
* for the y-axis.
*/
int segment(int low, int high,
int pos, int strip)
{
if (high == low) {
ini_seg[strip][pos] = rect[strip][low];
}
else {
int mid = (low + high) / 2;
segment(low, mid, 2 * pos, strip);
segment(mid + 1, high, 2 * pos + 1, strip);
ini_seg[strip][pos] = ini_seg[strip][2 * pos] +
ini_seg[strip][2 * pos + 1];
}
}
/*
* A recursive function that constructs
* Final Segment Tree for array ini_seg[][] = { }.
*/
int finalSegment(int low, int high, int pos)
{
if (high == low) {
for (int i = 1; i < 2 * size; i++)
fin_seg[pos][i] = ini_seg[low][i];
}
else {
int mid = (low + high) / 2;
finalSegment(low, mid, 2 * pos);
finalSegment(mid + 1, high, 2 * pos + 1);
for (int i = 1; i < 2 * size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
/*
* Return sum of elements in range from index
* x1 to x2 . It uses the final_seg[][] array
* created using finalsegment() function.
* 'pos' is index of current node in
* segment tree fin_seg[][].
*/
int finalQuery(int pos, int start, int end,
int x1, int x2, int node)
{
if (x2 < start || end < x1) {
return 0;
}
if (x1 <= start && end <= x2) {
return fin_seg[node][pos];
}
int mid = (start + end) / 2;
int p1 = finalQuery(2 * pos, start, mid,
x1, x2, node);
int p2 = finalQuery(2 * pos + 1, mid + 1,
end, x1, x2, node);
return (p1 + p2);
}
/*
* This function calls the finalQuery function
* for elements in range from index x1 to x2 .
* This function queries the yth coordinate.
*/
int query(int pos, int start, int end,
int y1, int y2, int x1, int x2)
{
if (y2 < start || end < y1) {
return 0;
}
if (y1 <= start && end <= y2) {
return (finalQuery(1, 1, 4, x1, x2, pos));
}
int mid = (start + end) / 2;
int p1 = query(2 * pos, start,
mid, y1, y2, x1, x2);
int p2 = query(2 * pos + 1, mid + 1,
end, y1, y2, x1, x2);
return (p1 + p2);
}
/* A recursive function to update the nodes
which for the given index. The following
are parameters : pos --> index of current
node in segment tree fin_seg[][]. x ->
index of the element to be updated. val -->
Value to be change at node idx
*/
int finalUpdate(int pos, int low, int high,
int x, int val, int node)
{
if (low == high) {
fin_seg[node][pos] = val;
}
else {
int mid = (low + high) / 2;
if (low <= x && x <= mid) {
finalUpdate(2 * pos, low, mid, x, val, node);
}
else {
finalUpdate(2 * pos + 1, mid + 1, high,
x, val, node);
}
fin_seg[node][pos] = fin_seg[node][2 * pos] +
fin_seg[node][2 * pos + 1];
}
}
/*
This function call the final update function after
visiting the yth coordinate in the segment tree fin_seg[][].
*/
int update(int pos, int low, int high, int x, int y, int val)
{
if (low == high) {
finalUpdate(1, 1, 4, x, val, pos);
}
else {
int mid = (low + high) / 2;
if (low <= y && y <= mid) {
update(2 * pos, low, mid, x, y, val);
}
else {
update(2 * pos + 1, mid + 1, high, x, y, val);
}
for (int i = 1; i < size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
// Driver program to test above functions
int main()
{
int pos = 1;
int low = 0;
int high = 3;
// Call the ini_segment() to create the
// initial segment tree on x- coordinate
for (int strip = 0; strip < 4; strip++)
segment(low, high, 1, strip);
// Call the final function to built the 2d segment tree.
finalSegment(low, high, 1);
/*
Query:
* To request the query for sub-rectangle y1, y2=(2, 3) x1, x2=(2, 3)
* update the value of index (3, 3)=100;
* To request the query for sub-rectangle y1, y2=(2, 3) x1, x2=(2, 3)
*/
cout << "The sum of the submatrix (y1, y2)->(2, 3), "
<< " (x1, x2)->(2, 3) is "
<< query(1, 1, 4, 2, 3, 2, 3) << endl;
// Function to update the value
update(1, 1, 4, 2, 3, 100);
cout << "The sum of the submatrix (y1, y2)->(2, 3), "
<< "(x1, x2)->(2, 3) is "
<< query(1, 1, 4, 2, 3, 2, 3) << endl;
return 0;
}
Java
// Java program for implementation
// of 2D segment tree.
import java.util.*;
class GfG
{
// Base node of segment tree.
static int ini_seg[][] = new int[1000][1000];
// final 2d-segment tree.
static int fin_seg[][] = new int[1000][1000];
// Rectangular matrix.
static int rect[][] = {{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 7, 5, 9 },
{ 3, 0, 6, 2 },
};
// size of x coordinate.
static int size = 4;
/*
* A recursive function that constructs
* Initial Segment Tree for array rect[][] = { }.
* 'pos' is index of current node in segment
* tree seg[]. 'strip' is the enumeration
* for the y-axis.
*/
static void segment(int low, int high,
int pos, int strip)
{
if (high == low)
{
ini_seg[strip][pos] = rect[strip][low];
}
else
{
int mid = (low + high) / 2;
segment(low, mid, 2 * pos, strip);
segment(mid + 1, high, 2 * pos + 1, strip);
ini_seg[strip][pos] = ini_seg[strip][2 * pos] +
ini_seg[strip][2 * pos + 1];
}
}
/*
* A recursive function that constructs
* Final Segment Tree for array ini_seg[][] = { }.
*/
static void finalSegment(int low, int high, int pos)
{
if (high == low)
{
for (int i = 1; i < 2 * size; i++)
fin_seg[pos][i] = ini_seg[low][i];
}
else
{
int mid = (low + high) / 2;
finalSegment(low, mid, 2 * pos);
finalSegment(mid + 1, high, 2 * pos + 1);
for (int i = 1; i < 2 * size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
/*
* Return sum of elements in range from index
* x1 to x2 . It uses the final_seg[][] array
* created using finalsegment() function.
* 'pos' is index of current node in
* segment tree fin_seg[][].
*/
static int finalQuery(int pos, int start, int end,
int x1, int x2, int node)
{
if (x2 < start || end < x1)
{
return 0;
}
if (x1 <= start && end <= x2)
{
return fin_seg[node][pos];
}
int mid = (start + end) / 2;
int p1 = finalQuery(2 * pos, start, mid,
x1, x2, node);
int p2 = finalQuery(2 * pos + 1, mid + 1,
end, x1, x2, node);
return (p1 + p2);
}
/*
* This function calls the finalQuery function
* for elements in range from index x1 to x2 .
* This function queries the yth coordinate.
*/
static int query(int pos, int start, int end,
int y1, int y2, int x1, int x2)
{
if (y2 < start || end < y1)
{
return 0;
}
if (y1 <= start && end <= y2)
{
return (finalQuery(1, 1, 4, x1, x2, pos));
}
int mid = (start + end) / 2;
int p1 = query(2 * pos, start,
mid, y1, y2, x1, x2);
int p2 = query(2 * pos + 1, mid + 1,
end, y1, y2, x1, x2);
return (p1 + p2);
}
/* A recursive function to update the nodes
which for the given index. The following
are parameters : pos --> index of current
node in segment tree fin_seg[][]. x ->
index of the element to be updated. val -->
Value to be change at node idx
*/
static void finalUpdate(int pos, int low, int high,
int x, int val, int node)
{
if (low == high)
{
fin_seg[node][pos] = val;
}
else
{
int mid = (low + high) / 2;
if (low <= x && x <= mid)
{
finalUpdate(2 * pos, low, mid, x, val, node);
}
else
{
finalUpdate(2 * pos + 1, mid + 1, high,
x, val, node);
}
fin_seg[node][pos] = fin_seg[node][2 * pos] +
fin_seg[node][2 * pos + 1];
}
}
/*
This function call the final
update function after visiting
the yth coordinate in the segment
tree fin_seg[][].
*/
static void update(int pos, int low,
int high, int x,
int y, int val)
{
if (low == high)
{
finalUpdate(1, 1, 4, x, val, pos);
}
else
{
int mid = (low + high) / 2;
if (low <= y && y <= mid)
{
update(2 * pos, low, mid, x, y, val);
}
else
{
update(2 * pos + 1, mid + 1, high, x, y, val);
}
for (int i = 1; i < size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
// Driver code
public static void main(String[] args)
{
int pos = 1;
int low = 0;
int high = 3;
// Call the ini_segment() to create the
// initial segment tree on x- coordinate
for (int strip = 0; strip < 4; strip++)
segment(low, high, 1, strip);
// Call the final function to
// built the 2d segment tree.
finalSegment(low, high, 1);
/*
Query:
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
* update the value of index (3, 3)=100;
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
*/
System.out.println("The sum of the submatrix (y1, y2)->(2, 3), "
+ " (x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3));
// Function to update the value
update(1, 1, 4, 2, 3, 100);
System.out.println("The sum of the submatrix (y1, y2)->(2, 3), "
+ "(x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3));
}
}
// This code has been contributed by 29AjayKumar
Python3
# Python 3 program for implementation
# of 2D segment tree.
# Base node of segment tree.
ini_seg = [[ 0 for x in range(1000)]
for y in range(1000)]
# final 2d-segment tree.
fin_seg = [[ 0 for x in range(1000)]
for y in range(1000)]
# Rectangular matrix.
rect= [[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 1, 7, 5, 9 ],
[ 3, 0, 6, 2 ]]
# size of x coordinate.
size = 4
'''
* A recursive function that constructs
* Initial Segment Tree for array rect[][] = { }.
* 'pos' is index of current node in segment
* tree seg[]. 'strip' is the enumeration
* for the y-axis.
'''
def segment(low, high, pos, strip):
if (high == low) :
ini_seg[strip][pos] = rect[strip][low]
else :
mid = (low + high) // 2
segment(low, mid, 2 * pos, strip)
segment(mid + 1, high, 2 * pos + 1, strip)
ini_seg[strip][pos] = (ini_seg[strip][2 * pos] +
ini_seg[strip][2 * pos + 1])
# A recursive function that constructs
# Final Segment Tree for array ini_seg[][] = { }.
def finalSegment(low, high, pos):
if (high == low) :
for i in range(1, 2 * size):
fin_seg[pos][i] = ini_seg[low][i]
else :
mid = (low + high) // 2
finalSegment(low, mid, 2 * pos)
finalSegment(mid + 1, high, 2 * pos + 1)
for i in range( 1, 2 * size):
fin_seg[pos][i] = (fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i])
'''
* Return sum of elements in range
* from index x1 to x2 . It uses the
* final_seg[][] array created using
* finalsegment() function. 'pos' is
* index of current node in segment
* tree fin_seg[][].
'''
def finalQuery(pos, start, end, x1, x2, node):
if (x2 < start or end < x1) :
return 0
if (x1 <= start and end <= x2) :
return fin_seg[node][pos]
mid = (start + end) // 2
p1 = finalQuery(2 * pos, start, mid,
x1, x2, node)
p2 = finalQuery(2 * pos + 1, mid + 1,
end, x1, x2, node)
return (p1 + p2)
'''
* This function calls the finalQuery function
* for elements in range from index x1 to x2 .
* This function queries the yth coordinate.
'''
def query(pos, start, end, y1, y2, x1, x2):
if (y2 < start or end < y1) :
return 0
if (y1 <= start and end <= y2) :
return (finalQuery(1, 1, 4, x1, x2, pos))
mid = (start + end) // 2
p1 = query(2 * pos, start, mid,
y1, y2, x1, x2)
p2 = query(2 * pos + 1, mid + 1,
end, y1, y2, x1, x2)
return (p1 + p2)
''' A recursive function to update the nodes
which for the given index. The following
are parameters : pos --> index of current
node in segment tree fin_seg[][]. x ->
index of the element to be updated. val -->
Value to be change at node idx
'''
def finalUpdate(pos, low, high, x, val, node):
if (low == high) :
fin_seg[node][pos] = val
else :
mid = (low + high) // 2
if (low <= x and x <= mid) :
finalUpdate(2 * pos, low, mid,
x, val, node)
else :
finalUpdate(2 * pos + 1, mid + 1,
high, x, val, node)
fin_seg[node][pos] = (fin_seg[node][2 * pos] +
fin_seg[node][2 * pos + 1])
# This function call the final
# update function after visiting
# the yth coordinate in the
# segment tree fin_seg[][].
def update(pos, low, high, x, y, val):
if (low == high) :
finalUpdate(1, 1, 4, x, val, pos)
else :
mid = (low + high) // 2
if (low <= y and y <= mid) :
update(2 * pos, low, mid, x, y, val)
else :
update(2 * pos + 1, mid + 1,
high, x, y, val)
for i in range(1, size):
fin_seg[pos][i] = (fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i])
# Driver Code
if __name__ == "__main__":
pos = 1
low = 0
high = 3
# Call the ini_segment() to create the
# initial segment tree on x- coordinate
for strip in range(4):
segment(low, high, 1, strip)
# Call the final function to built
# the 2d segment tree.
finalSegment(low, high, 1)
'''
Query:
* To request the query for sub-rectangle
* y1, y2=(2, 3) x1, x2=(2, 3)
* update the value of index (3, 3)=100;
* To request the query for sub-rectangle
* y1, y2=(2, 3) x1, x2=(2, 3)
'''
print( "The sum of the submatrix (y1, y2)->(2, 3), ",
"(x1, x2)->(2, 3) is ", query(1, 1, 4, 2, 3, 2, 3))
# Function to update the value
update(1, 1, 4, 2, 3, 100)
print( "The sum of the submatrix (y1, y2)->(2, 3), ",
"(x1, x2)->(2, 3) is ", query(1, 1, 4, 2, 3, 2, 3))
C#
// C# program for implementation
// of 2D segment tree.
using System;
class GfG
{
// Base node of segment tree.
static int [,]ini_seg = new int[1000, 1000];
// final 2d-segment tree.
static int [,]fin_seg = new int[1000, 1000];
// Rectangular matrix.
static int [,]rect = {{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 1, 7, 5, 9 },
{ 3, 0, 6, 2 },
};
// size of x coordinate.
static int size = 4;
/*
* A recursive function that constructs
* Initial Segment Tree for array rect[,] = { }.
* 'pos' is index of current node in segment
* tree seg[]. 'strip' is the enumeration
* for the y-axis.
*/
static void segment(int low, int high,
int pos, int strip)
{
if (high == low)
{
ini_seg[strip, pos] = rect[strip, low];
}
else
{
int mid = (low + high) / 2;
segment(low, mid, 2 * pos, strip);
segment(mid + 1, high, 2 * pos + 1, strip);
ini_seg[strip,pos] = ini_seg[strip, 2 * pos] +
ini_seg[strip, 2 * pos + 1];
}
}
/*
* A recursive function that constructs
* Final Segment Tree for array ini_seg[,] = { }.
*/
static void finalSegment(int low, int high, int pos)
{
if (high == low)
{
for (int i = 1; i < 2 * size; i++)
fin_seg[pos, i] = ini_seg[low, i];
}
else
{
int mid = (low + high) / 2;
finalSegment(low, mid, 2 * pos);
finalSegment(mid + 1, high, 2 * pos + 1);
for (int i = 1; i < 2 * size; i++)
fin_seg[pos,i] = fin_seg[2 * pos, i] +
fin_seg[2 * pos + 1, i];
}
}
/*
* Return sum of elements in range from index
* x1 to x2 . It uses the final_seg[,] array
* created using finalsegment() function.
* 'pos' is index of current node in
* segment tree fin_seg[,].
*/
static int finalQuery(int pos, int start, int end,
int x1, int x2, int node)
{
if (x2 < start || end < x1)
{
return 0;
}
if (x1 <= start && end <= x2)
{
return fin_seg[node, pos];
}
int mid = (start + end) / 2;
int p1 = finalQuery(2 * pos, start, mid,
x1, x2, node);
int p2 = finalQuery(2 * pos + 1, mid + 1,
end, x1, x2, node);
return (p1 + p2);
}
/*
* This function calls the finalQuery function
* for elements in range from index x1 to x2 .
* This function queries the yth coordinate.
*/
static int query(int pos, int start, int end,
int y1, int y2, int x1, int x2)
{
if (y2 < start || end < y1)
{
return 0;
}
if (y1 <= start && end <= y2)
{
return (finalQuery(1, 1, 4, x1, x2, pos));
}
int mid = (start + end) / 2;
int p1 = query(2 * pos, start,
mid, y1, y2, x1, x2);
int p2 = query(2 * pos + 1, mid + 1,
end, y1, y2, x1, x2);
return (p1 + p2);
}
/* A recursive function to update the nodes
which for the given index. The following
are parameters : pos --> index of current
node in segment tree fin_seg[,]. x ->
index of the element to be updated. val -->
Value to be change at node idx
*/
static void finalUpdate(int pos, int low, int high,
int x, int val, int node)
{
if (low == high)
{
fin_seg[node, pos] = val;
}
else
{
int mid = (low + high) / 2;
if (low <= x && x <= mid)
{
finalUpdate(2 * pos, low, mid, x, val, node);
}
else
{
finalUpdate(2 * pos + 1, mid + 1, high,
x, val, node);
}
fin_seg[node,pos] = fin_seg[node, 2 * pos] +
fin_seg[node, 2 * pos + 1];
}
}
/*
This function call the final
update function after visiting
the yth coordinate in the segment
tree fin_seg[,].
*/
static void update(int pos, int low,
int high, int x,
int y, int val)
{
if (low == high)
{
finalUpdate(1, 1, 4, x, val, pos);
}
else
{
int mid = (low + high) / 2;
if (low <= y && y <= mid)
{
update(2 * pos, low, mid, x, y, val);
}
else
{
update(2 * pos + 1, mid + 1, high, x, y, val);
}
for (int i = 1; i < size; i++)
fin_seg[pos,i] = fin_seg[2 * pos, i] +
fin_seg[2 * pos + 1, i];
}
}
// Driver code
public static void Main()
{
int pos = 1;
int low = 0;
int high = 3;
// Call the ini_segment() to create the
// initial segment tree on x- coordinate
for (int strip = 0; strip < 4; strip++)
segment(low, high, 1, strip);
// Call the final function to
// built the 2d segment tree.
finalSegment(low, high, 1);
/*
Query:
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
* update the value of index (3, 3)=100;
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
*/
Console.WriteLine("The sum of the submatrix (y1, y2)->(2, 3), "
+ " (x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3));
// Function to update the value
update(1, 1, 4, 2, 3, 100);
Console.WriteLine("The sum of the submatrix (y1, y2)->(2, 3), "
+ "(x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3));
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// Javascript program for implementation
// of 2D segment tree.
// Base node of segment tree.
let ini_seg = new Array(1000);
// final 2d-segment tree.
let fin_seg = new Array(1000);
for(let i = 0; i < 1000; i++)
{
ini_seg[i] = new Array(1000);
fin_seg[i] = new Array(1000);
for(let j = 0; j < 1000; j++)
{
ini_seg[i][j] = 0;
fin_seg[i][j] = 0;
}
}
// Rectangular matrix.
let rect = [[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 1, 7, 5, 9 ],
[ 3, 0, 6, 2 ]];
// size of x coordinate.
let size = 4;
/*
* A recursive function that constructs
* Initial Segment Tree for array rect[][] = { }.
* 'pos' is index of current node in segment
* tree seg[]. 'strip' is the enumeration
* for the y-axis.
*/
function segment(low,high,pos,strip)
{
if (high == low)
{
ini_seg[strip][pos] = rect[strip][low];
}
else
{
let mid = Math.floor((low + high) / 2);
segment(low, mid, 2 * pos, strip);
segment(mid + 1, high, 2 * pos + 1, strip);
ini_seg[strip][pos] = ini_seg[strip][2 * pos] +
ini_seg[strip][2 * pos + 1];
}
}
/*
* A recursive function that constructs
* Final Segment Tree for array ini_seg[][] = { }.
*/
function finalSegment(low,high,pos)
{
if (high == low)
{
for (let i = 1; i < 2 * size; i++)
fin_seg[pos][i] = ini_seg[low][i];
}
else
{
let mid = Math.floor((low + high) / 2);
finalSegment(low, mid, 2 * pos);
finalSegment(mid + 1, high, 2 * pos + 1);
for (let i = 1; i < 2 * size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
/*
* Return sum of elements in range from index
* x1 to x2 . It uses the final_seg[][] array
* created using finalsegment() function.
* 'pos' is index of current node in
* segment tree fin_seg[][].
*/
function finalQuery(pos,start,end,x1,x2,node)
{
if (x2 < start || end < x1)
{
return 0;
}
if (x1 <= start && end <= x2)
{
return fin_seg[node][pos];
}
let mid = Math.floor((start + end) / 2);
let p1 = finalQuery(2 * pos, start, mid,
x1, x2, node);
let p2 = finalQuery(2 * pos + 1, mid + 1,
end, x1, x2, node);
return (p1 + p2);
}
/*
* This function calls the finalQuery function
* for elements in range from index x1 to x2 .
* This function queries the yth coordinate.
*/
function query(pos,start,end,y1,y2,x1,x2)
{
if (y2 < start || end < y1)
{
return 0;
}
if (y1 <= start && end <= y2)
{
return (finalQuery(1, 1, 4, x1, x2, pos));
}
let mid = Math.floor((start + end) / 2);
let p1 = query(2 * pos, start,
mid, y1, y2, x1, x2);
let p2 = query(2 * pos + 1, mid + 1,
end, y1, y2, x1, x2);
return (p1 + p2);
}
/* A recursive function to update the nodes
which for the given index. The following
are parameters : pos --> index of current
node in segment tree fin_seg[][]. x ->
index of the element to be updated. val -->
Value to be change at node idx
*/
function finalUpdate(pos,low,high,x,val,node)
{
if (low == high)
{
fin_seg[node][pos] = val;
}
else
{
let mid = Math.floor((low + high) / 2);
if (low <= x && x <= mid)
{
finalUpdate(2 * pos, low, mid, x, val, node);
}
else
{
finalUpdate(2 * pos + 1, mid + 1, high,
x, val, node);
}
fin_seg[node][pos] = fin_seg[node][2 * pos] +
fin_seg[node][2 * pos + 1];
}
}
/*
This function call the final
update function after visiting
the yth coordinate in the segment
tree fin_seg[][].
*/
function update(pos,low,high,x,y,val)
{
if (low == high)
{
finalUpdate(1, 1, 4, x, val, pos);
}
else
{
let mid = Math.floor((low + high) / 2);
if (low <= y && y <= mid)
{
update(2 * pos, low, mid, x, y, val);
}
else
{
update(2 * pos + 1, mid + 1, high, x, y, val);
}
for (let i = 1; i < size; i++)
fin_seg[pos][i] = fin_seg[2 * pos][i] +
fin_seg[2 * pos + 1][i];
}
}
// Driver code
let pos = 1;
let low = 0;
let high = 3;
// Call the ini_segment() to create the
// initial segment tree on x- coordinate
for (let strip = 0; strip < 4; strip++)
segment(low, high, 1, strip);
// Call the final function to
// built the 2d segment tree.
finalSegment(low, high, 1);
/*
Query:
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
* update the value of index (3, 3)=100;
* To request the query for sub-rectangle
y1, y2=(2, 3) x1, x2=(2, 3)
*/
document.write("The sum of the submatrix (y1, y2)->(2, 3), "
+ " (x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3)+"<br>");
// Function to update the value
update(1, 1, 4, 2, 3, 100);
document.write("The sum of the submatrix (y1, y2)->(2, 3), "
+ "(x1, x2)->(2, 3) is "
+ query(1, 1, 4, 2, 3, 2, 3)+"<br>");
// This code is contributed by rag2127
</script>
The sum of the submatrix (y1, y2)->(2, 3), (x1, x2)->(2, 3) is 25 The sum of the submatrix (y1, y2)->(2, 3), (x1, x2)->(2, 3) is 118
Complejidad de tiempo:
Consulta de procesamiento: O(logn*logm)
Consulta de modificación: O(2*n*logn*logm)
Complejidad de espacio: O(4*m*n)
Publicación traducida automáticamente
Artículo escrito por sumit.chauhan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA