Dado un equipo de N jugadores. ¿Cuántos juegos mínimos se requieren para encontrar al segundo mejor jugador?
Podemos usar argumentos adversarios basados en el árbol del torneo (montón binario). Un árbol de torneo es una forma de montón mínimo (máximo) que es un árbol binario completo. Cada Node externo representa a un jugador y el Node interno representa al ganador.
En un árbol de torneo, cada Node interno contiene al ganador y cada Node hoja contiene un jugador. Habrá N – 1 Node interno en un árbol binario con N Nodes de hoja (externos).
Para obtener más detalles, consulte esta publicación (ponga n = 2 en la ecuación dada en la publicación). Es obvio que para seleccionar al mejor jugador entre N jugadores, se deben eliminar (N – 1) jugadores, es decir, necesitamos un mínimo de (N – 1) juegos (comparaciones). Matemáticamente podemos demostrarlo. En un árbol binario, I = E – 1, donde I es un número de Nodes internos y E es un número de Nodes externos. Significa encontrar el elemento máximo o mínimo de una array, necesitamos comparaciones N – 1 (Nodes internos).
Segundo mejor jugador La información explorada durante la selección del mejor jugador se puede utilizar para minimizar el número de comparaciones al rastrear a los siguientes mejores jugadores. Por ejemplo, podemos elegir al segundo mejor jugador en (N + log 2 N – 2) comparaciones. El siguiente diagrama muestra un árbol de torneos (árbol de ganadores ) como un montón máximo. Tenga en cuenta que el concepto del árbol perdedor es diferente.
El árbol anterior contiene 4 Nodes de hojas que representan a los jugadores y tienen 3 niveles 0, 1 y 2. Inicialmente, se realizan 2 juegos en el nivel 2, uno entre 5 y 3 y otro entre 7 y 8. En el siguiente movimiento, uno Se realiza más juego entre 5 y 8 para concluir el ganador final. En general, necesitamos 3 comparaciones.
Para el segundo mejor jugador, necesitamos rastrear a los candidatos que participaron con el ganador final, lo que lleva a 7 como el segundo mejor.
La mediana de las arrays ordenadas El árbol del torneo se puede usar de manera efectiva para encontrar la mediana de las arrays ordenadas. Supongamos, dadas M arrays ordenadas de igual tamaño L (por simplicidad). Podemos adjuntar todas estas arrays ordenadas al árbol del torneo, una array por hoja. Necesitamos un árbol de altura CEIL (log 2 M) para tener al menos M Nodes externos. Considere un ejemplo. Dados 3 (M = 3) arreglos de enteros ordenados de tamaño máximo de 5 elementos.
{ 2, 5, 7, 11, 15 } ---- Array1
{1, 3, 4} ---- Array2
{6, 8, 12, 13, 14} ---- Array3
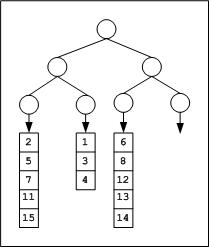
¿Cuál debería ser la altura del árbol del torneo? Necesitamos construir un árbol de torneo de altura log 2 3 .= 1.585 = 2 redondeado al siguiente entero. Un árbol binario de altura 2 tendrá 4 hojas a las que podemos adjuntar las arrays como se muestra en la siguiente figura.
Después del primer torneo, el árbol aparece como se muestra a continuación,
Podemos observar que el ganador es de Array2. Por lo tanto, el siguiente elemento de Array2 se sumergirá y los juegos se jugarán a lo largo de la ruta ganadora del torneo anterior.
Tenga en cuenta que el infinito se utiliza como elemento centinela. Según los datos que se mantienen en los Nodes, podemos seleccionar el carácter centinela. Por ejemplo, generalmente almacenamos los punteros en Nodes en lugar de claves, por lo que NULL puede servir como centinela. Si alguno de los arreglos se agota, llenaremos la hoja correspondiente y los próximos Nodes internos con centinela. Después del segundo torneo, el árbol aparece como se muestra a continuación,
El próximo ganador es de Array1, por lo que el siguiente elemento de la array Array1, que es 5, se sumergirá en la siguiente ronda y el próximo torneo se jugará en el camino de 2. Los torneos pueden continuar hasta que obtengamos el elemento mediano que es ( 5+3+5)/2 = 7mo elemento.
Tenga en cuenta que existen algoritmos aún mejores para encontrar la mediana de la unión de arrays ordenadas; para obtener más información, consulte los enlaces relacionados que se proporcionan a continuación.
En general, con M listas ordenadas de tamaño L 1 , L 2 … L m requiere una complejidad de tiempo de O((L 1 + L 2 + … + L m ) * logM) para fusionar todas las arrays y O(m*logM) tiempo para encontrar la mediana, donde m es la posición de la mediana.
elegir el millón de elementos más pequeño de un billón de elementos sin ordenar: como una solución simple, podemos ordenar mil millones de números y seleccionar el primer millón. En un sistema de memoria limitada, clasificar mil millones de elementos y elegir el primer millón parece poco práctico. Podemos utilizar el enfoque del árbol de torneos. En cualquier momento, solo los elementos de un árbol están en la memoria.
Divida la array grande (quizás almacenada en el disco) en arrays de menor tamaño de un millón cada una (o incluso más pequeñas que la máquina pueda clasificar). Ordene estas 1000 arrays de tamaño pequeño y guárdelas en el disco como archivos individuales. Construya un árbol de torneo que pueda tener al menos 1000 Nodes de hoja (el árbol debe tener una altura de 10 ya que 2 9 < 1000 < 2 10 , si el tamaño del archivo individual es aún más pequeño, necesitaremos más Nodes de hoja). Cada Node de hoja tendrá un motor que selecciona el siguiente elemento del archivo ordenado almacenado en el disco.
Podemos jugar el juego del árbol del torneo para extraer el primer millón de elementos. Costo total = clasificar 1000 listas de un millón cada una + construcción de árboles + torneos.
Aplicación de árboles de torneo:
- Se utiliza para fines de clasificación.
- Se utiliza para encontrar el elemento más grande y más pequeño.
- También se puede usar en fusiones m-way
- Aplicado en el problema de carga de camiones
Implementación:
Necesitamos construir el árbol de abajo hacia arriba. Todos los Nodes hoja se llenaron primero. Comience en el extremo izquierdo del árbol y rellene a lo largo de la anchura (es decir, de 2 k-1 a 2 k – 1 donde k es la profundidad del árbol) y juegue el juego. Después de practicar con algunos ejemplos, será fácil escribir código. La implementación se analiza en el siguiente código. Segundo elemento mínimo usando comparaciones mínimas .
Publicaciones relacionadas : encuentre el elemento más pequeño y el segundo más pequeño en una array . Segundo elemento mínimo usando comparaciones mínimas — por Venki .
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA