Árbol rojo negro vs árbol AVL

En esta publicación, compararemos Red-Black Tree y AVL Tree. 

Árbol negro rojo : 

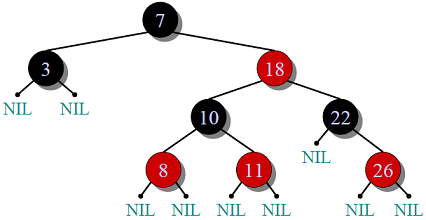
Propiedades : 
 

1. El autoequilibrio se proporciona pintando cada Node con dos colores (rojo o negro).
2. Cuando se modifica el árbol, se reorganiza y pinta un nuevo árbol.
3. Requiere 1 bit de información de color para cada Node en el árbol.
4. Complejidad temporal: O(logn).

Restricciones mantenidas por Red Black Tree : 
 

1. La raíz siempre es negra.
2. Todas las hojas NULL son negras y los dos hijos de un Node rojo son negros.
3. Todo camino simple desde un Node dado a cualquiera de sus hojas descendientes contiene el mismo número de 
   Nodes negros.
4. El camino desde la raíz hasta la hoja más lejana no es más del doble que el camino desde la raíz hasta la hoja más cercana.
5. Complejidad temporal: O(logn).

Árbol AVL (Adelson-Velskii y Landis) 

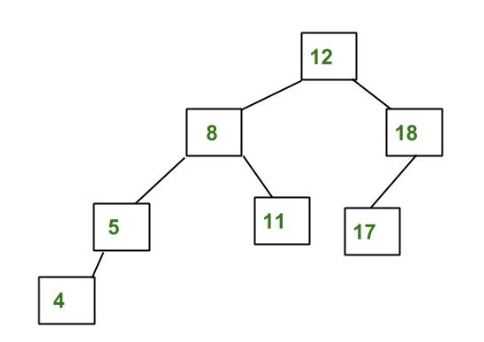
Propiedades : 
 

1. La diferencia de altura del subárbol izquierdo y derecho del Node debe ser inferior a 2.
2. El reequilibrio se realiza cuando las alturas de dos subárboles secundarios de un Node difieren en más de uno.
3. Recuperaciones más rápidas como estrictamente equilibradas.

diferencia : 

Base de comparación	Árboles negros rojos	Árboles AVL
búsquedas	Red Black Trees tiene menos búsquedas porque no están estrictamente equilibrados.	Los árboles AVL proporcionan búsquedas más rápidas que los árboles rojo-negro porque están más estrictamente equilibrados.
Color	En esto, el color del Node es rojo o negro.	En esto, no hay color del Node.
Inserción y extracción	Red Black Trees proporciona operaciones de inserción y eliminación más rápidas que los árboles AVL, ya que se realizan menos rotaciones debido a un equilibrio relativamente relajado.	Los árboles AVL proporcionan operaciones complejas de inserción y eliminación a medida que se realizan más rotaciones debido a un equilibrio relativamente relajado.
Almacenamiento	Red Black Tree requiere solo 1 bit de información por Node.	Los árboles AVL almacenan factores de equilibrio o alturas con cada Node, por lo que requieren almacenamiento para un número entero por Node.
buscando	No proporciona una búsqueda eficiente.	Proporciona una búsqueda eficiente.
Usos	Los árboles rojo-negro se utilizan en la mayoría de las bibliotecas de idiomas, como map, multimap, multiset en C++, etc.	Los árboles AVL se utilizan en bases de datos donde se requieren recuperaciones más rápidas.
Factor de equilibrio	No da factor de equilibrio	Cada Node tiene un factor de equilibrio cuyo valor será 1,0,-1
Equilibrio	Tome menos procesamiento para equilibrar, es decir; máximo dos rotaciones requeridas	Tome más procesamiento para equilibrar